Тема: Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница. Интегрирование по частям и заменой переменной в определенном интеграле.
6.1. Интеграл с переменным верхним пределом.
Пусть 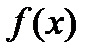 непрерывная функция на отрезке
непрерывная функция на отрезке  . Рассмотрим интеграл
. Рассмотрим интеграл  , где верхний предел
, где верхний предел 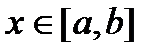 . Верхний предел x и x под знаком интеграла разные и имеют разный смысл. Верхний предел x является произвольной фиксированной точкой отрезка
. Верхний предел x и x под знаком интеграла разные и имеют разный смысл. Верхний предел x является произвольной фиксированной точкой отрезка  , а x под знаком интеграла является переменной, которая изменяется от a до верхнего предела x. Интеграл
, а x под знаком интеграла является переменной, которая изменяется от a до верхнего предела x. Интеграл  называется интегралом с переменным верхним пределом, т.к. верхний предел x может принимать любое значение из отрезка
называется интегралом с переменным верхним пределом, т.к. верхний предел x может принимать любое значение из отрезка  . По условию
. По условию 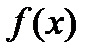 непрерывна на любом отрезке
непрерывна на любом отрезке 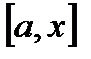 ,
, 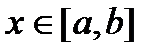 , то по теореме существования интеграл
, то по теореме существования интеграл  существует для любого
существует для любого 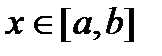 , поэтому
, поэтому 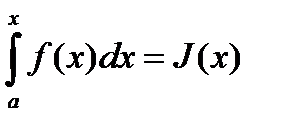 является функцией от x.
является функцией от x.
Далее покажем, что функция 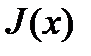 является дифференцируемой функцией.
является дифференцируемой функцией.
Теорема. Если 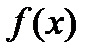 непрерывна на отрезке
непрерывна на отрезке  , то производная от интеграла с переменным верхним пределом равна подынтегральной функции, т.е.
, то производная от интеграла с переменным верхним пределом равна подынтегральной функции, т.е. 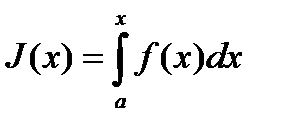 является первообразной для подынтегральной функции на
является первообразной для подынтегральной функции на  ,
, 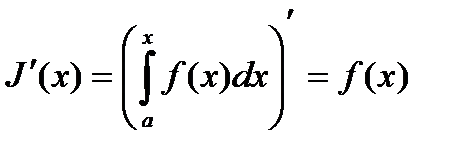
Доказательство.
По определению производной 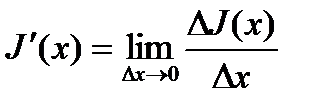
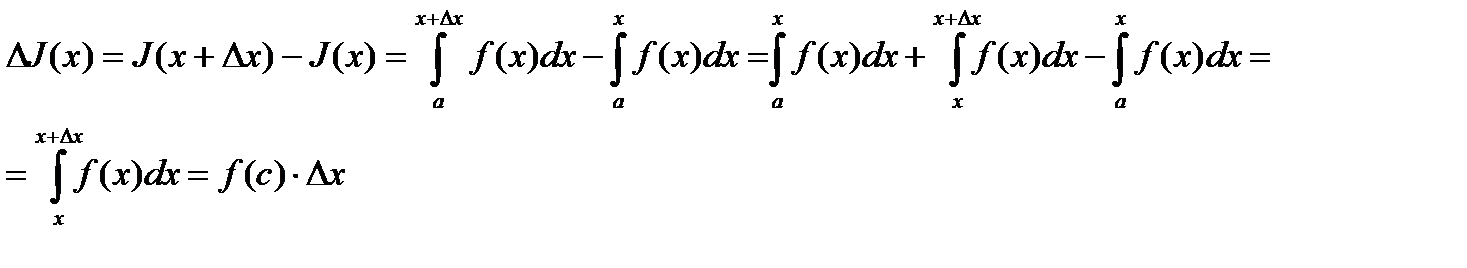
где с расположено между 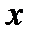 и
и 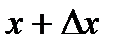 .
.
Последнее равенство имеет место в силу теоремы о среднем. Подставляя вместо 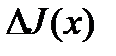 полученное выражение, будем иметь
полученное выражение, будем иметь
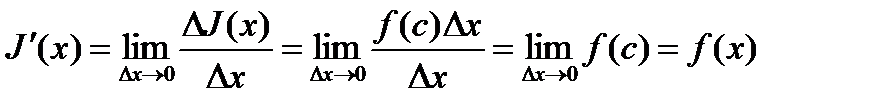 .
.
Точка с расположена между 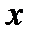 и
и 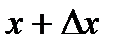 , поэтому
, поэтому 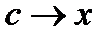 при
при 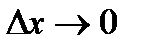 . Так как
. Так как 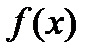 непрерывна в точке x, то
непрерывна в точке x, то 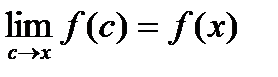 . ▼
. ▼
6.2. Формула Ньютона-Лейбница.
Теорема. Справедлива формула 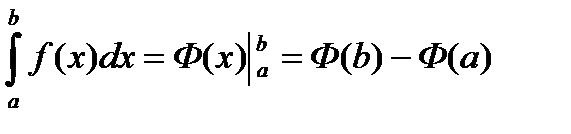 , где Ф(x) какая-либо первообразная для подынтегральной функции
, где Ф(x) какая-либо первообразная для подынтегральной функции 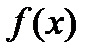 .
.
Доказательство.
Рассмотрим интеграл с переменным верхним пределом 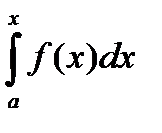 . Этот интеграл является первообразной для функции
. Этот интеграл является первообразной для функции 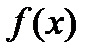 . Пусть
. Пусть 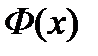 – произвольная другая первообразная для
– произвольная другая первообразная для 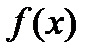 . Две различные первообразные для функции
. Две различные первообразные для функции 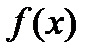 различаются на константу. Поэтому
различаются на константу. Поэтому 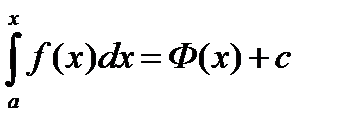 . Положим верхний предел
. Положим верхний предел 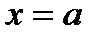 , тогда получим:
, тогда получим: 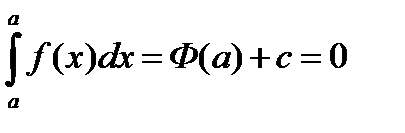 , отсюда
, отсюда 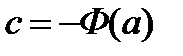 ,
, 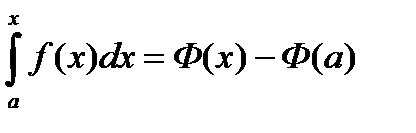 . В последнем интеграле вместо верхнего предела x подставим
. В последнем интеграле вместо верхнего предела x подставим 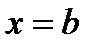 , тогда получим:
, тогда получим: 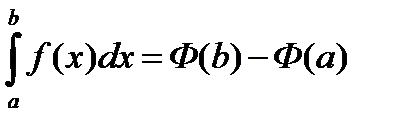 . ▼
. ▼
Пример. Вычислить 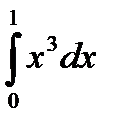
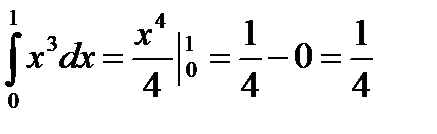
6.3. Интегрирование по частям в определенном интеграле.
Теорема. Справедлива формула 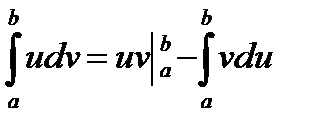 .
.
Доказательство. Имеем: 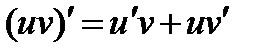 .
.
Почленно проинтегрируем последнее равенство

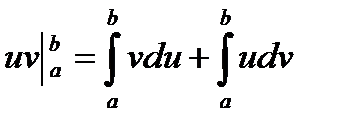
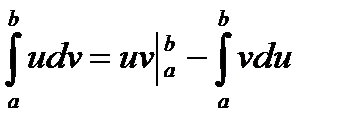 . ▼
. ▼
Пример. Вычислить 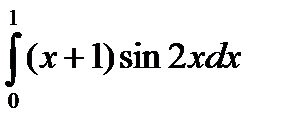
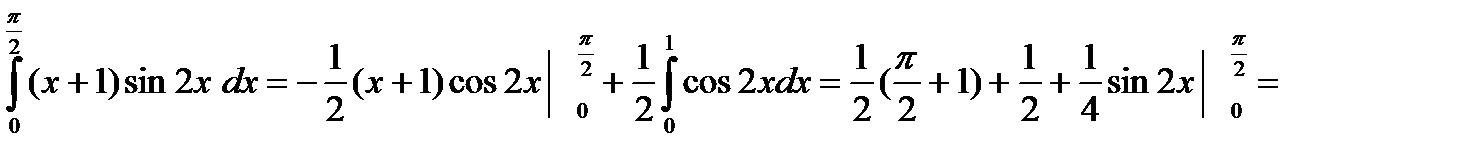
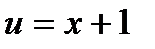
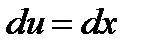
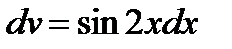
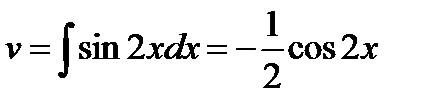
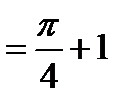 .
.
Пример. Вычислить 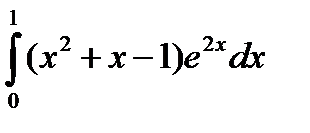
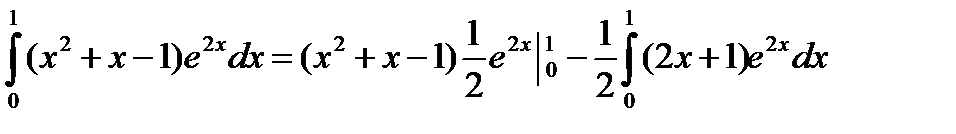
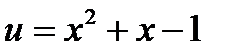 ;
; 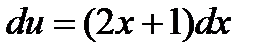
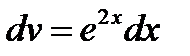 ;
; 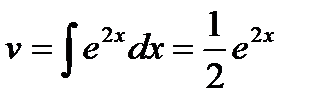
К последнему интегралу применим еще раз формулу интегрирование по частям.
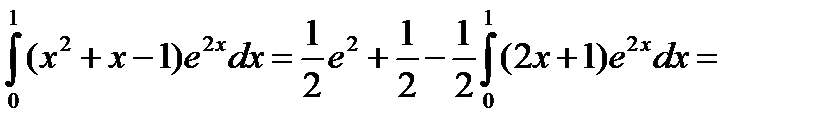
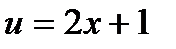 ;
; 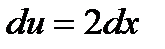
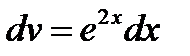 ;
; 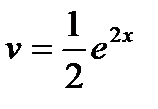
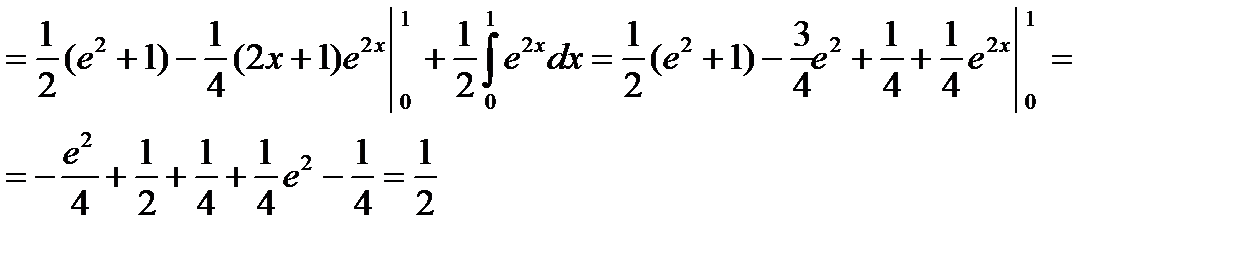
Пример. Вычислить 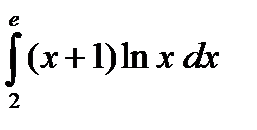
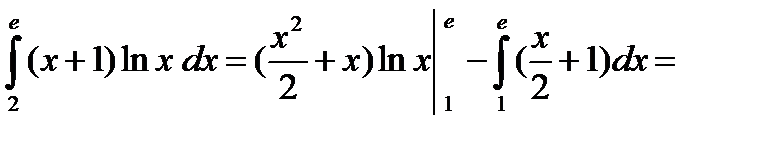
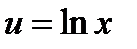 ;
; 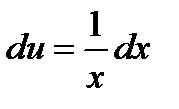
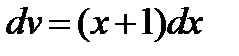 ;
; 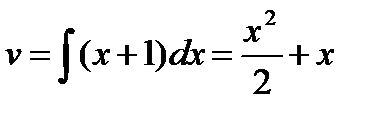
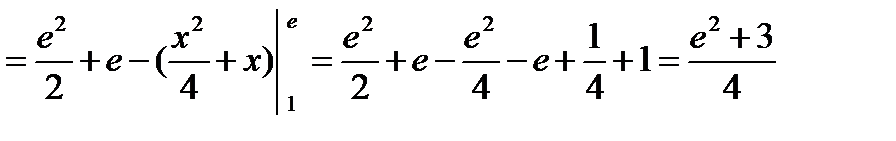
6.4. Замена переменной в определенном интеграле.
Пусть 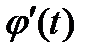 непрерывна на отрезке
непрерывна на отрезке 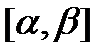 и
и 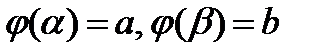 , а функция
, а функция 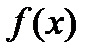 непрерывна на отрезке
непрерывна на отрезке  .
.
Справедлива формула
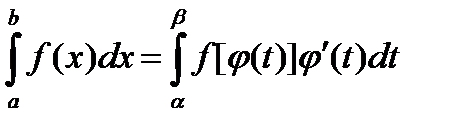 .
.
Доказательство. Так как 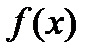 непрерывна на
непрерывна на  , то она на этом отрезке имеет первообразную, которую обозначим
, то она на этом отрезке имеет первообразную, которую обозначим 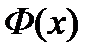 .
.
Функция 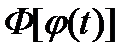 является первообразной для функции
является первообразной для функции 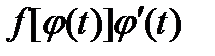 на отрезке
на отрезке 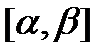 .
.
В самом деле, применяя правило дифференцирования сложной функции, получим: 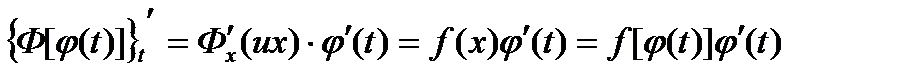 , где
, где 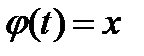 .
.
Используя формулу Ньютона-Лейбница, получим: 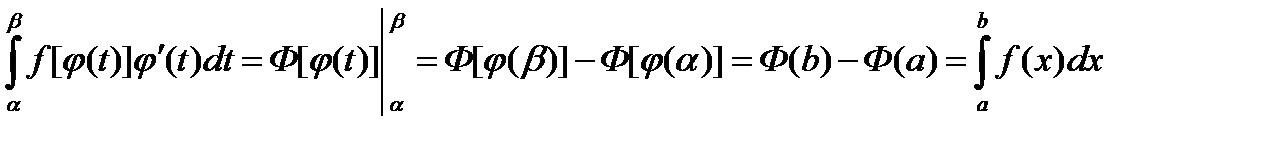 . ▼
. ▼
Пример. Вычислить 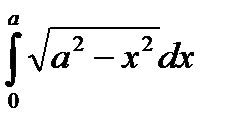
Сделаем замену 
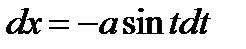
Если 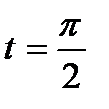 , то
, то 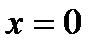 , если
, если  , то
, то 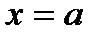
Следовательно, 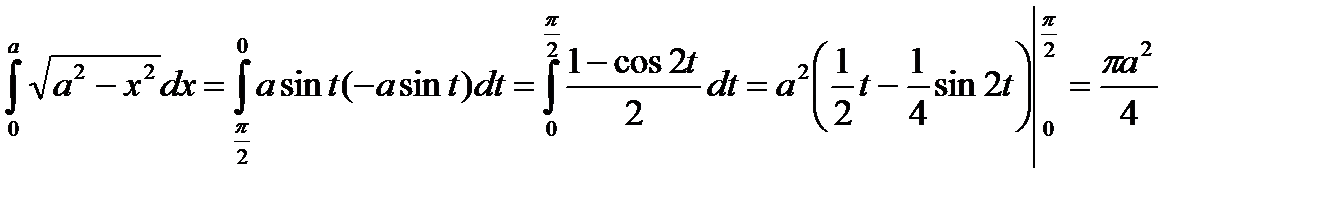
Дата добавления: 2015-08-21; просмотров: 2236;
