Тема: Интегрирование простейших рациональных дробей. Интегрирование тригонометрических выражений.
3.1. Интегрирование простейших рациональных дробей.

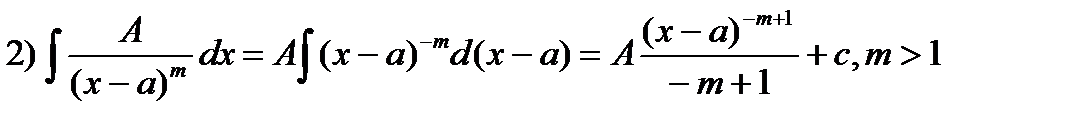
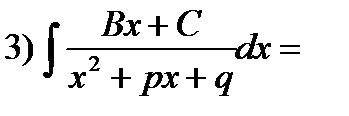
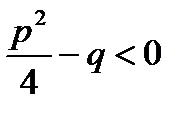
Выделим в числителе производную знаменателя
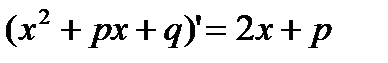
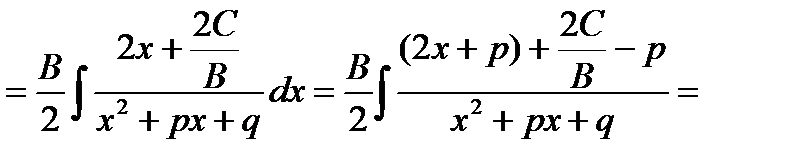

В подынтегральной функции в знаменателе выделим полный квадрат
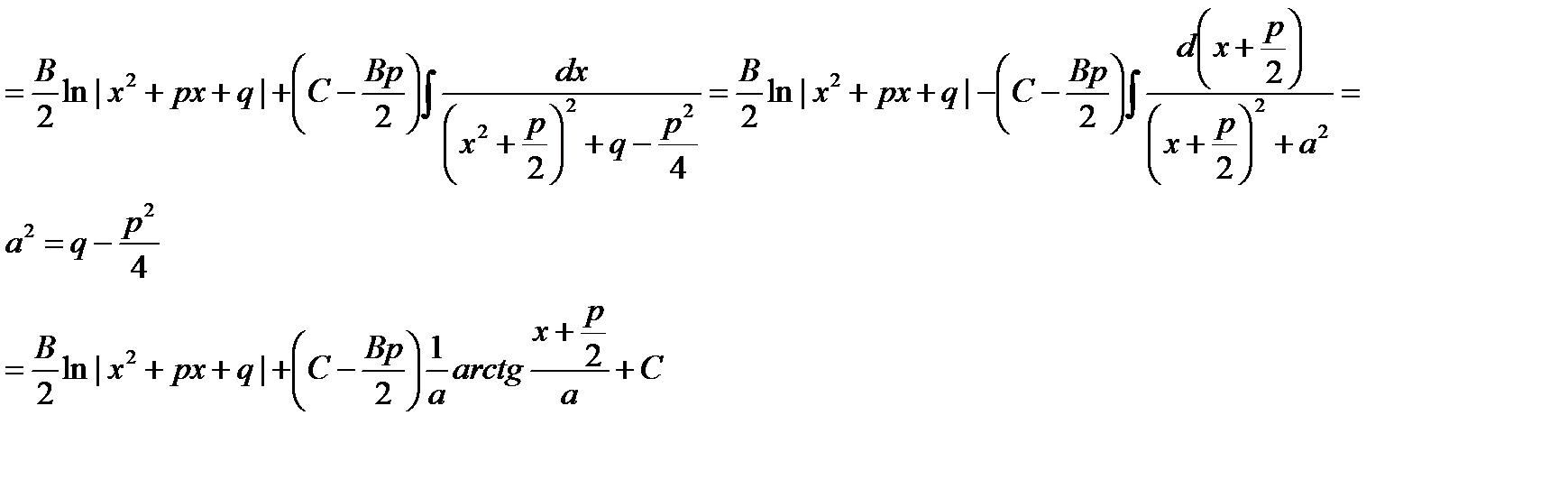
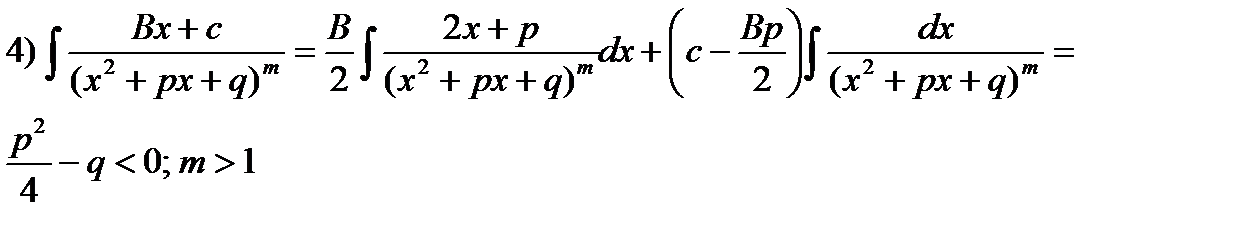
Сначала в числителе выделим производную квадратного трехчлена
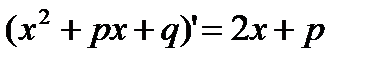
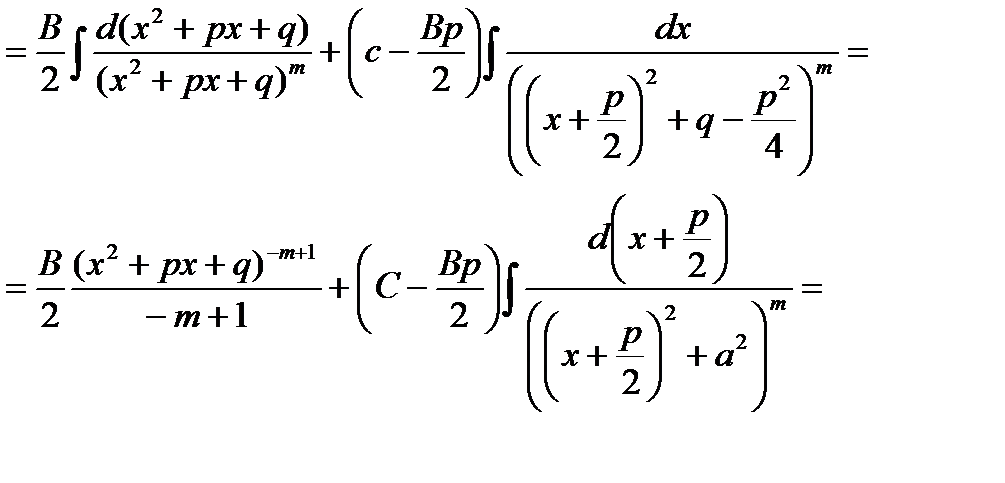
В последнем интеграле сделаем замену переменной 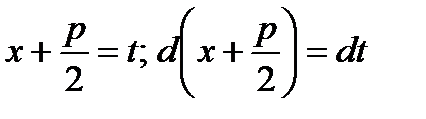
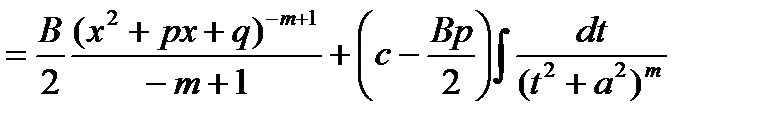
Нам остается вычислить интеграл
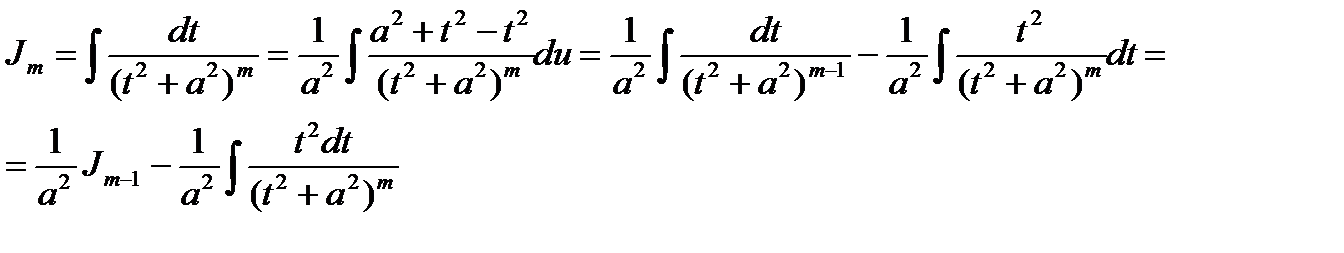
К последнему интегралу применим формулу интегрирования по частям
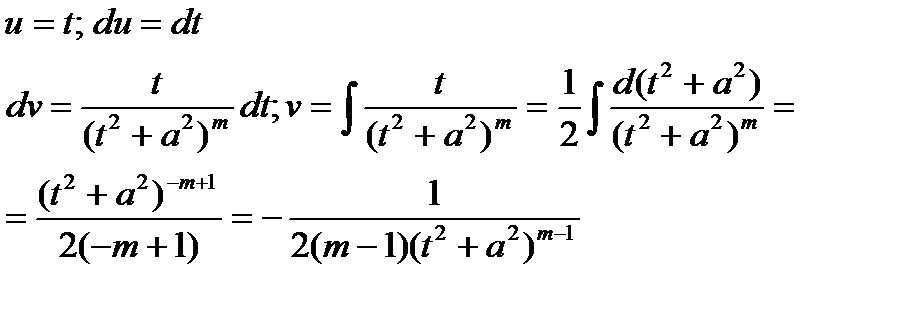
В результате получим
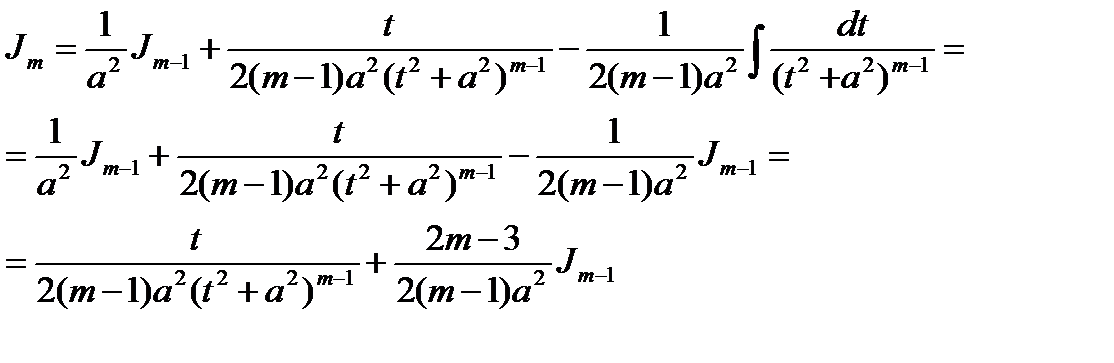
Итак, мы получили рекуррентную (возвратную) формулу
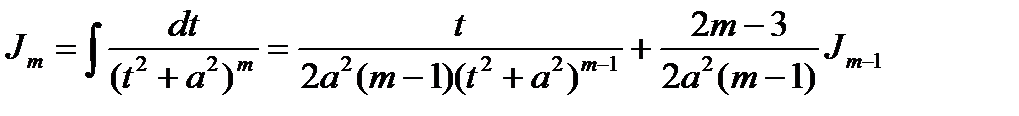
Применяя рекуррентную формулу вычисления интеграла 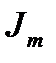 можно свести к вычислению интеграла
можно свести к вычислению интеграла 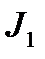
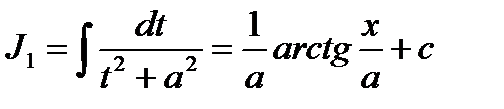
Пример. Вычислить. 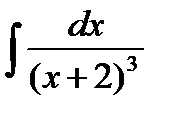 . В данном интеграле
. В данном интеграле 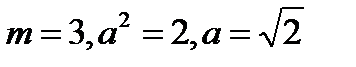
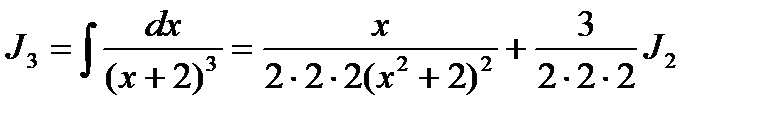 , где
, где 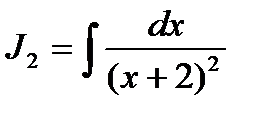 .
.
Для вычисления 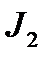 снова применим рекуррентную формулу, где
снова применим рекуррентную формулу, где 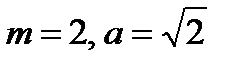 .
.
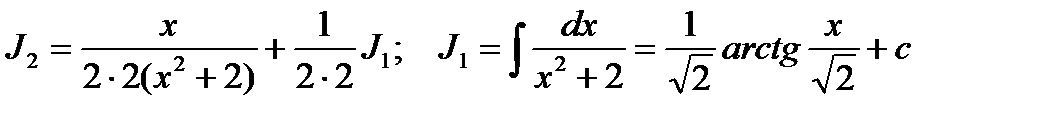
Учитывая полученное, будем иметь:
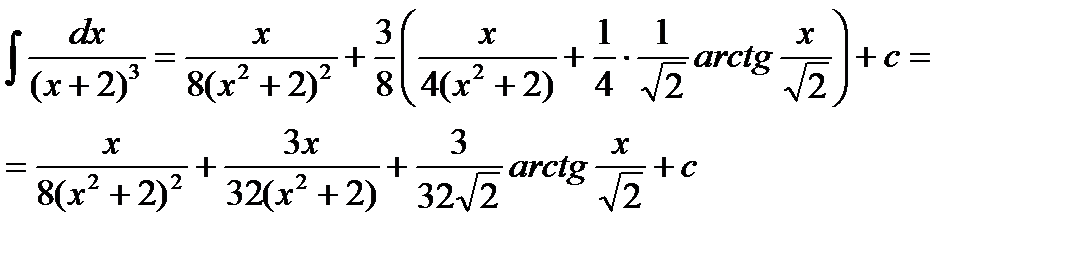
Пример. Вычислить интеграл 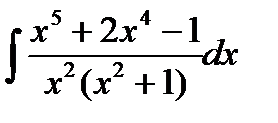 . Во-первых, отметим, что подынтегральная функция является неправильной рациональной дробью, т.к. степень числителя больше степени знаменателя, поэтому поделим числитель на знаменатель и представим данную неправильную рациональную дробь в виде суммы многочлена и правильной рациональной дроби.
. Во-первых, отметим, что подынтегральная функция является неправильной рациональной дробью, т.к. степень числителя больше степени знаменателя, поэтому поделим числитель на знаменатель и представим данную неправильную рациональную дробь в виде суммы многочлена и правильной рациональной дроби.
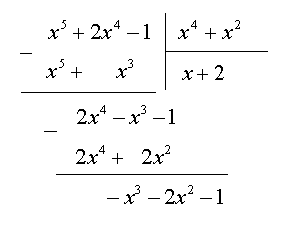
Итак, имеем:
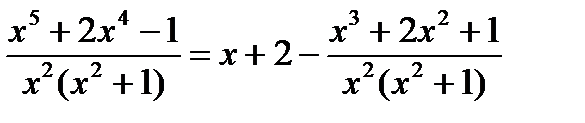
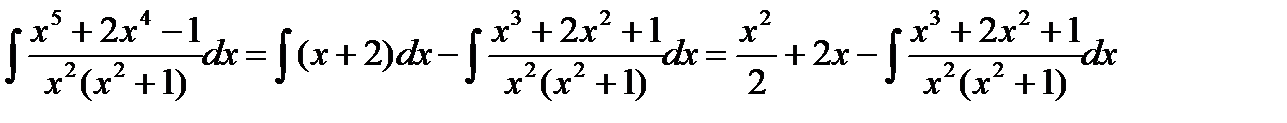
Теперь остается вычислить интеграл 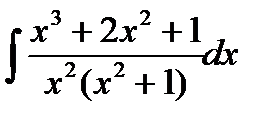 от правильной рациональной дроби. Для этого подынтегральную правильную рациональную дробь представили в виде суммы простейших рациональных дробей
от правильной рациональной дроби. Для этого подынтегральную правильную рациональную дробь представили в виде суммы простейших рациональных дробей
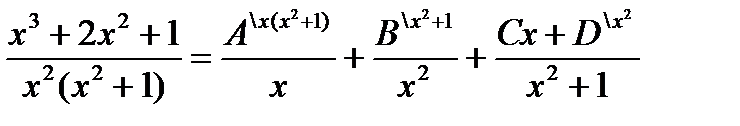
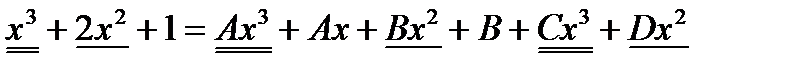
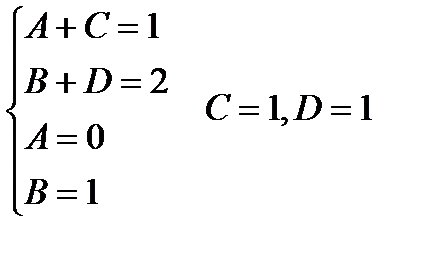
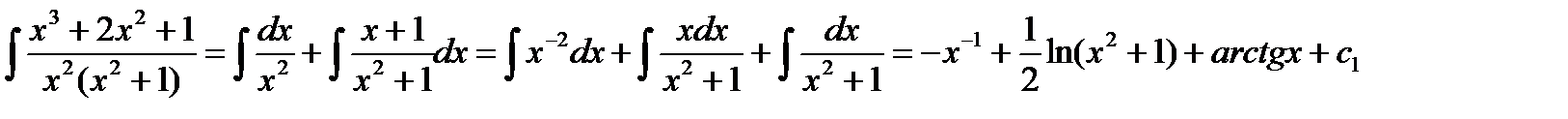
Учитывая полученный результат, будем иметь:
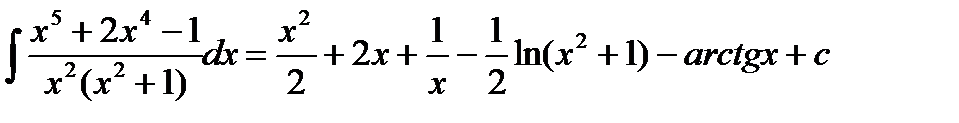
3.2. Интегрирование тригонометрических выражений.
Мы будем рассматривать
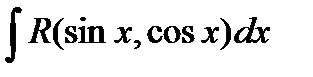 , где
, где 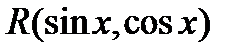 есть рациональная функция от
есть рациональная функция от 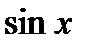 и
и  . Т.е. если положить
. Т.е. если положить 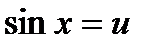 , a
, a 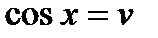 , то
, то 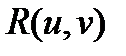 есть отношение двух многочленов от
есть отношение двух многочленов от  .
.
Например:
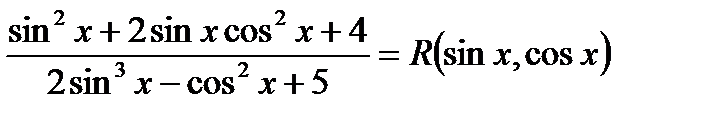
Далее функция
 не является рациональной функцией от
не является рациональной функцией от 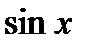 и
и  , т.к.
, т.к. 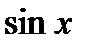 входит под знак корня.
входит под знак корня.
3.2.1. Универсальная подстановка.
Интеграл 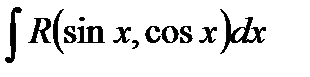 с помощью подстановки
с помощью подстановки 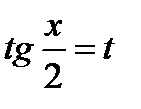 всегда сводится к интегралу от рациональной функции:
всегда сводится к интегралу от рациональной функции:
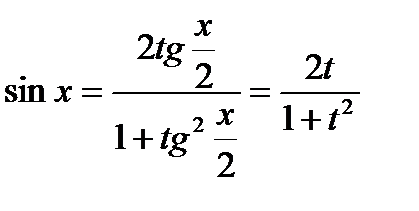
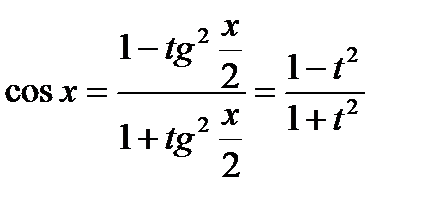
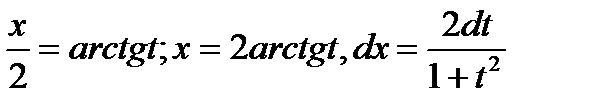
В результате получаем:
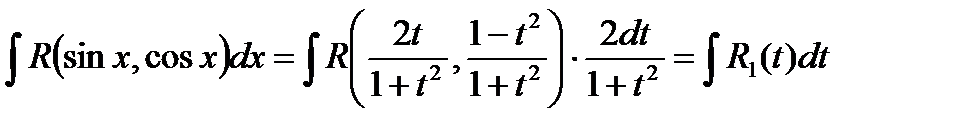
Пример. Вычислить интеграл 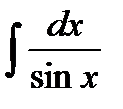 , пользуясь указанной заменой переменной
, пользуясь указанной заменой переменной 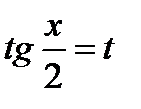 ,
, 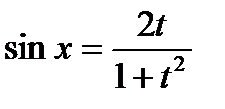 ,
,  , получим:
, получим:
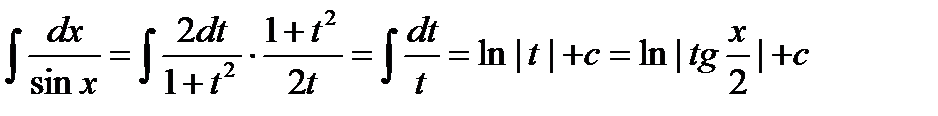
Пример. Вычислить интеграл 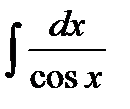
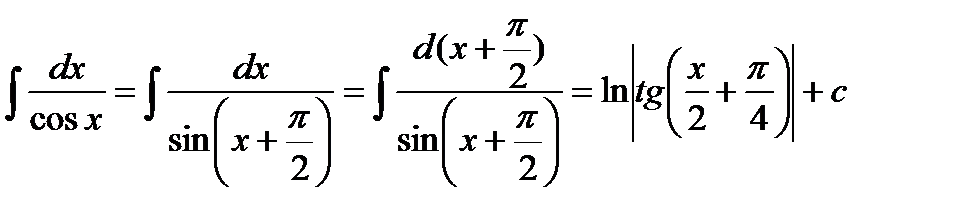
3.2.2. Теперь предположим, что 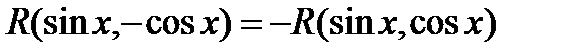 , т.е. подынтегральная функция нечетная относительно
, т.е. подынтегральная функция нечетная относительно  . В этом случае имеем:
. В этом случае имеем:
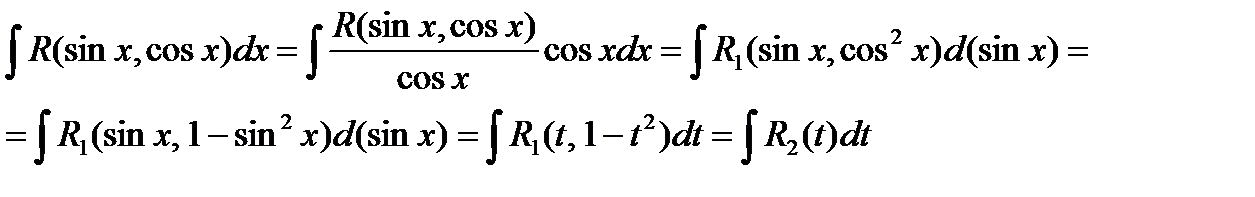
В этом случае была сделана замена 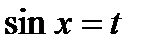 , и вычисление данного интеграла сводится к вычислению интеграла от рациональной функции.
, и вычисление данного интеграла сводится к вычислению интеграла от рациональной функции.
Пример. Вычислить интеграл:
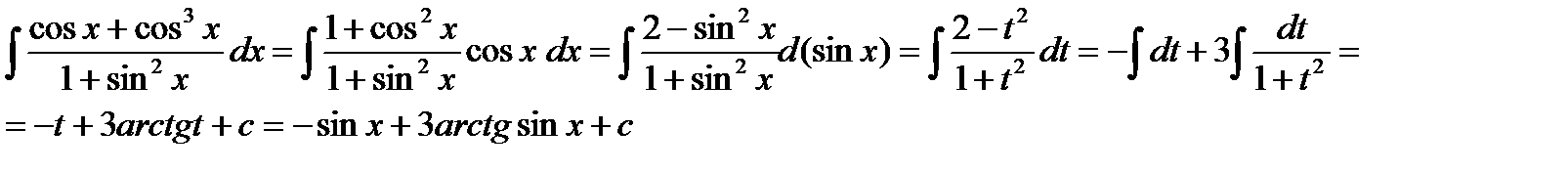
3.2.3. Пусть 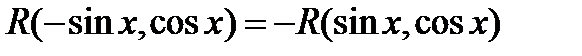 , т.е. подынтегральная функция нечетная относительно
, т.е. подынтегральная функция нечетная относительно 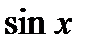 . В этом случае замена
. В этом случае замена 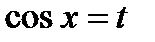 сводит вычисление
сводит вычисление 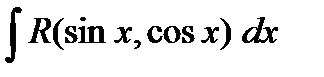 к вычислению интеграла от рациональной функции.
к вычислению интеграла от рациональной функции.
3.2.4. Теперь рассмотрим тот случай, когда
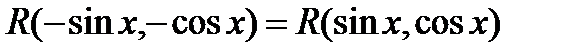 , т.е. подынтегральная функция четная относительно
, т.е. подынтегральная функция четная относительно 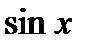 и
и 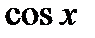 одновременно. В этом случае замена
одновременно. В этом случае замена 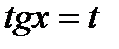 позволяет свести вычисление интеграла
позволяет свести вычисление интеграла 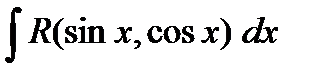 к вычислению интеграла от рациональной функции. В самом деле,
к вычислению интеграла от рациональной функции. В самом деле,
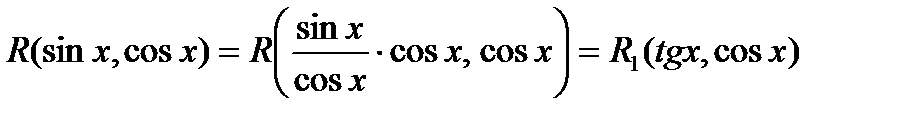 , т.к.
, т.к.
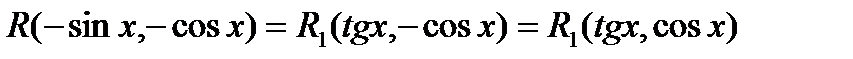 , то функция
, то функция  является четной относительно
является четной относительно 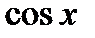 , поэтому
, поэтому 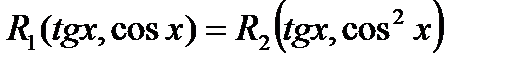 и
и
 .
.
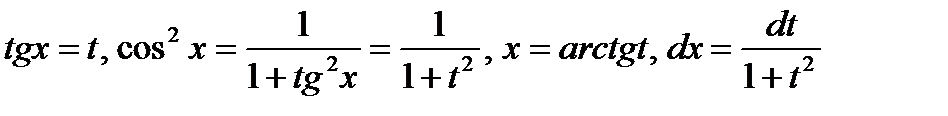
В результате замены переменной получим:
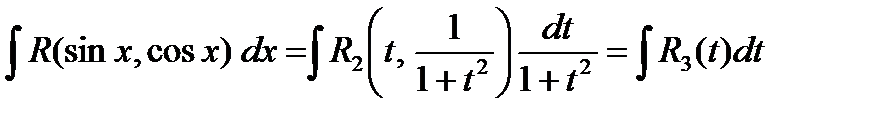
Пример. Вычислить интеграл 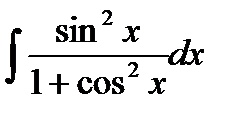 .
.
Подынтегральная функция является четной относительно 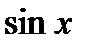 и
и  одновременно. Поэтому можно применить подстановку:
одновременно. Поэтому можно применить подстановку: 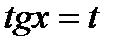 ,
, 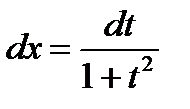 . Имеем:
. Имеем:
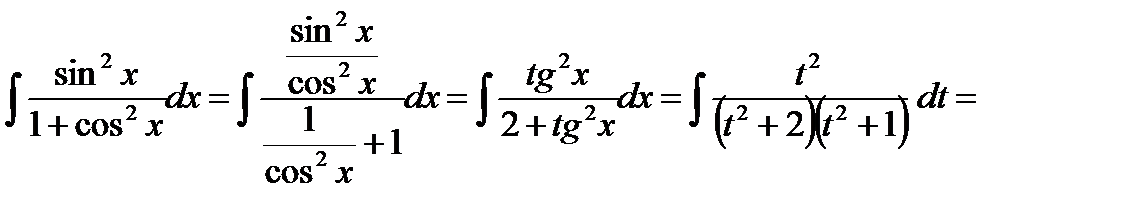
В последнем интеграле подынтегральная функция является правильной рациональной дробью, которую представим в виде суммы простейших рациональных дробей
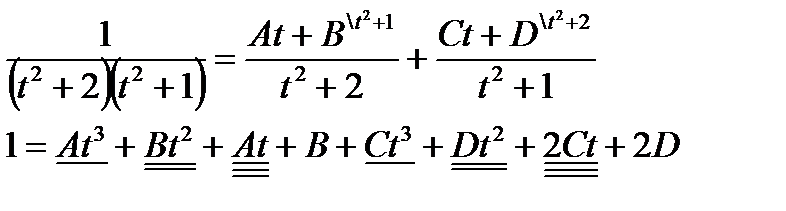
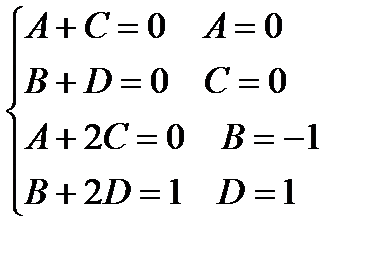
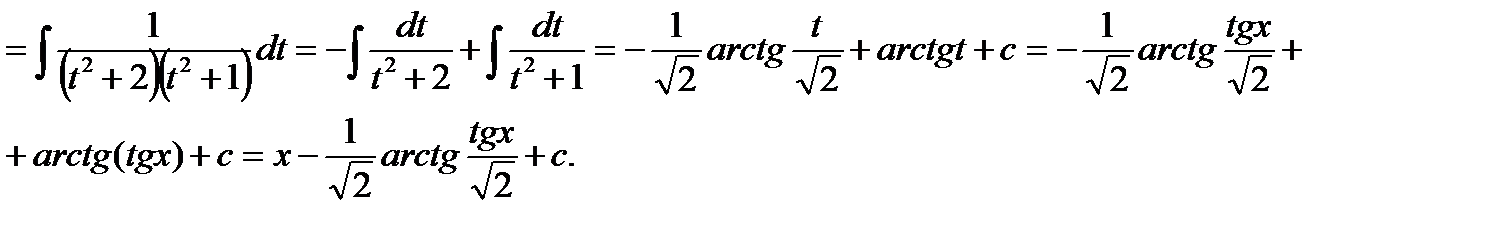
Дата добавления: 2015-08-21; просмотров: 1393;
