Лекция 2.
Лекция 1.
Тема: Первообразная. Определение неопределенного интеграла, его свойства. Таблица интегралов. Замена переменной в неопределенном интеграле.
1.1. Первообразная
Определение. Первообразной для функции 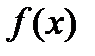 в интервале
в интервале 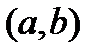 называется функция
называется функция 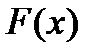 , производная которой равна
, производная которой равна  , т.е.
, т.е. 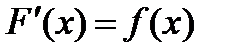 .
.
Пример. Найти первообразную для функции 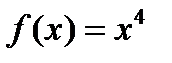 ,
, 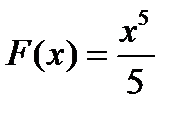 , так как
, так как 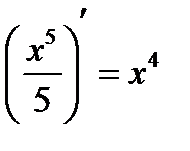 . Легко заметить, что любая функция
. Легко заметить, что любая функция 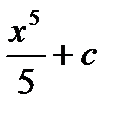 является первообразной для функции
является первообразной для функции 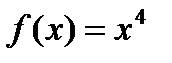 , где
, где  – const.
– const.
Таким образом, если функция 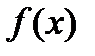 имеет одну первообразную
имеет одну первообразную 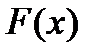 , то
, то 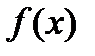 имеет бесконечно много первообразных
имеет бесконечно много первообразных 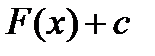 т.к.
т.к. 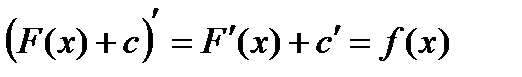 .
.
Теорема: Если функция 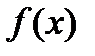 в интервале имеет первообразную
в интервале имеет первообразную 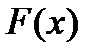 , то любая другая первообразная отличается от данной на константу.
, то любая другая первообразная отличается от данной на константу.
Доказательство: Пусть 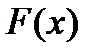 и
и  – две первообразные для функции
– две первообразные для функции 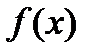 в интервале
в интервале 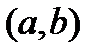 , т.е.
, т.е. 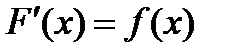 и
и 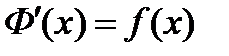 . Рассмотрим функцию
. Рассмотрим функцию 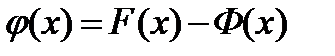 .
.
Функция 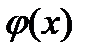 дифференцируема в интервале
дифференцируема в интервале 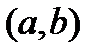 как разность двух дифференцируемых функций. Следовательно,
как разность двух дифференцируемых функций. Следовательно, 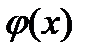 непрерывна в интервале
непрерывна в интервале 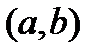 . Рассмотрим произвольный отрезок
. Рассмотрим произвольный отрезок  принадлежащий
принадлежащий 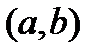 . Функция
. Функция 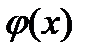 непрерывна на отрезке
непрерывна на отрезке 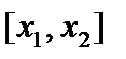 , дифференцируема в интервале
, дифференцируема в интервале 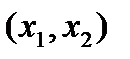 . Следовательно,
. Следовательно, 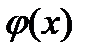 на отрезке
на отрезке 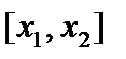 удовлетворяет всем условиям теоремы Лагранжа, по которой выполняется равенство
удовлетворяет всем условиям теоремы Лагранжа, по которой выполняется равенство 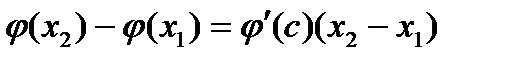 , где
, где 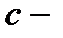 некоторая точка интервала
некоторая точка интервала 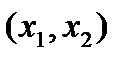 .
.
Имеем 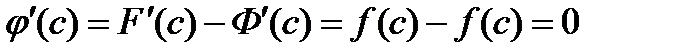 .Поэтому
.Поэтому 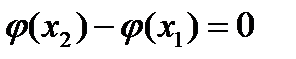 и
и 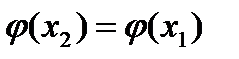 . Отсюда следует, что
. Отсюда следует, что 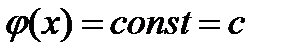 и
и 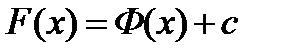 . ▼
. ▼
В дальнейшем будет доказано, что всякая непрерывная функция имеет первообразную.
1.2. Определение неопределенного интеграла и его свойства.
Определение: Неопределенным интегралом для функции 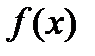 называют совокупность всех ее первообразных
называют совокупность всех ее первообразных 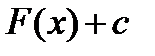 .
.
Неопределенный интеграл обозначается 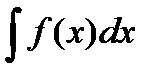 .
.
 , где
, где 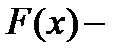 какая-либо одна из первообразных для
какая-либо одна из первообразных для  .
. 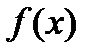 называется подынтегральной функцией,
называется подынтегральной функцией, 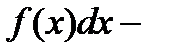 подынтегральным выражением.
подынтегральным выражением.
Свойства неопределенного интеграла:
1. 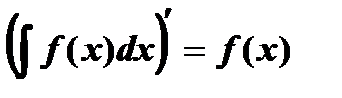
Доказательство. Пусть  одна из первообразных функции
одна из первообразных функции 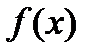 , тогда
, тогда 
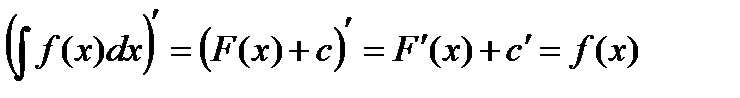 .
.
Таким образом, действие интегрирования проверяется дифференцированием.
2. 
Свойство 2 вытекает из свойства 1.
3.Постоянный множитель можно выносить за знак неопределенного интеграла.
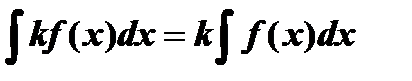
4. 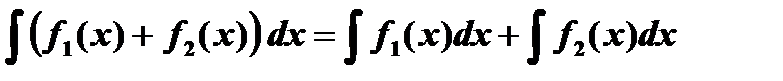 .
.
Таблица интегралов.
Из определения интеграла и формул дифференцирования функций следуют равенства:
1) 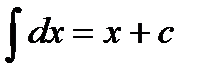 2)
2) 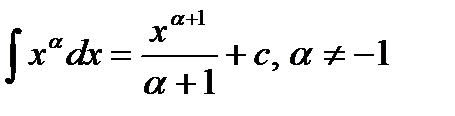 3)
3) 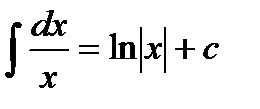 4)
4) 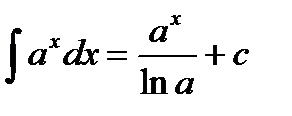 5)
5) 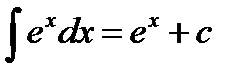 6)
6) 
| 7) 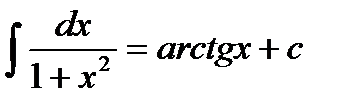 8)
8) 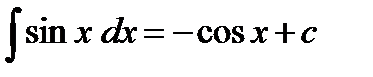 9)
9) 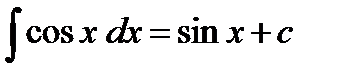 10)
10) 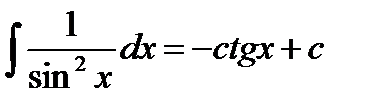 11)
11) 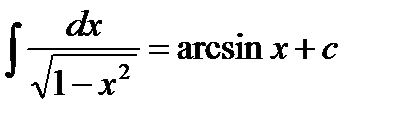
|
Все формулы проверяются дифференцированием.
Так из равенства:
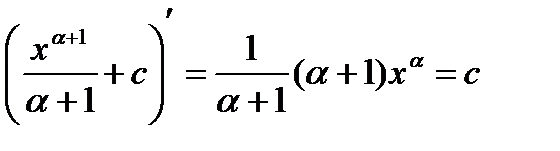
следует справедливость второй формулы.
Проверим теперь формулу 3 при  .
.
Имеем: 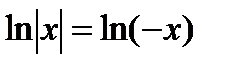 и
и 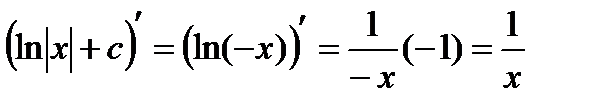 .
.
В последнем равенстве применили правило дифференцирования сложной функции.
1.3. Замена переменной в неопределенном интеграле.
Замена переменной в неопределенном интеграле есть действие обратное дифференцированию сложной функции.
Справедливо равенство:
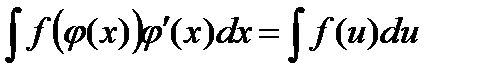 , где
, где 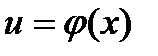 (1)
(1)
В самом деле, пусть 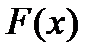 первообразная для
первообразная для 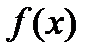 тогда
тогда
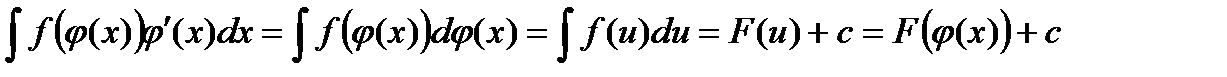
Использование формулы (1) слева направо называется подведением под знак дифференциала.
Приведем некоторые примеры:
Пример
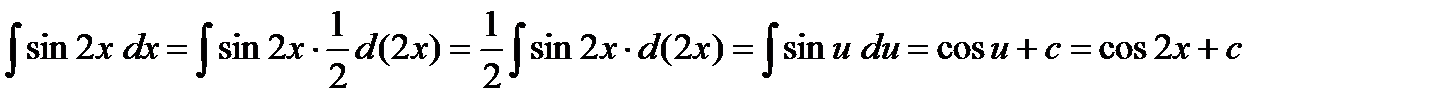 , где
, где 
В данном примере подводим под знак дифференциала 2х
Имеем: 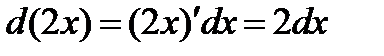 отсюда
отсюда 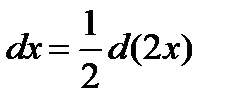 .
.
Пример 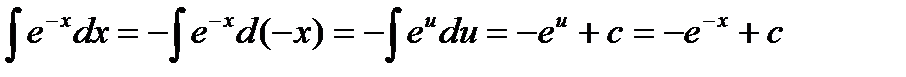 , где
, где 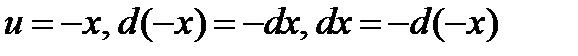
Пример
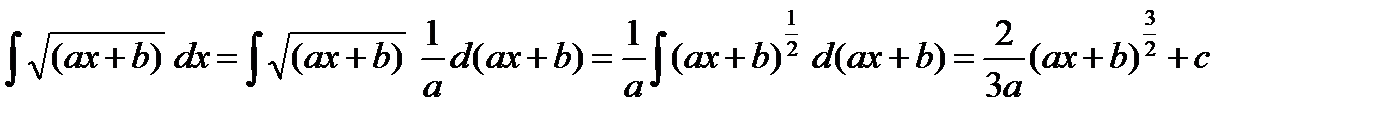

Пример
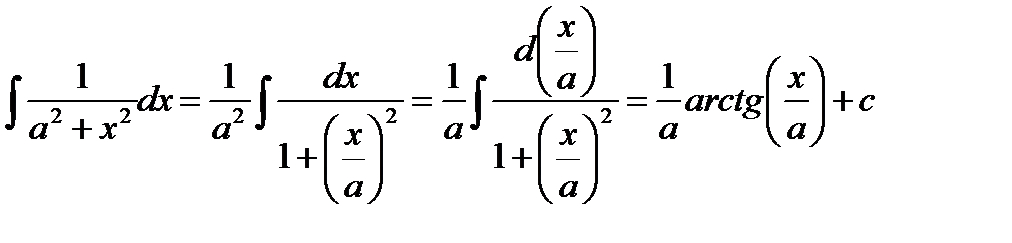 , т.к.
, т.к. 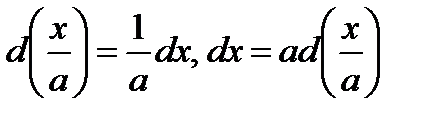
В дальнейшем мы покажем использование формулы (1) замены переменной справа налево.
Лекция 2.
Дата добавления: 2015-08-21; просмотров: 997;
