Тема: Вычисление площадей плоских фигур. Вычисление объемов тел.
8.1. Вычисление площадей плоских фигур.
8.1.1. Вычисление площади фигуры в декартовой системе координат.
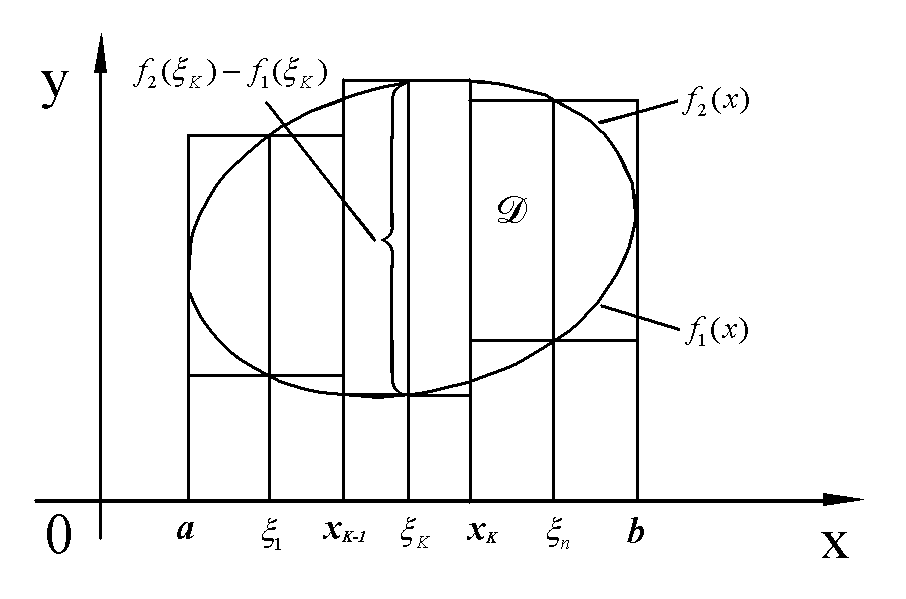
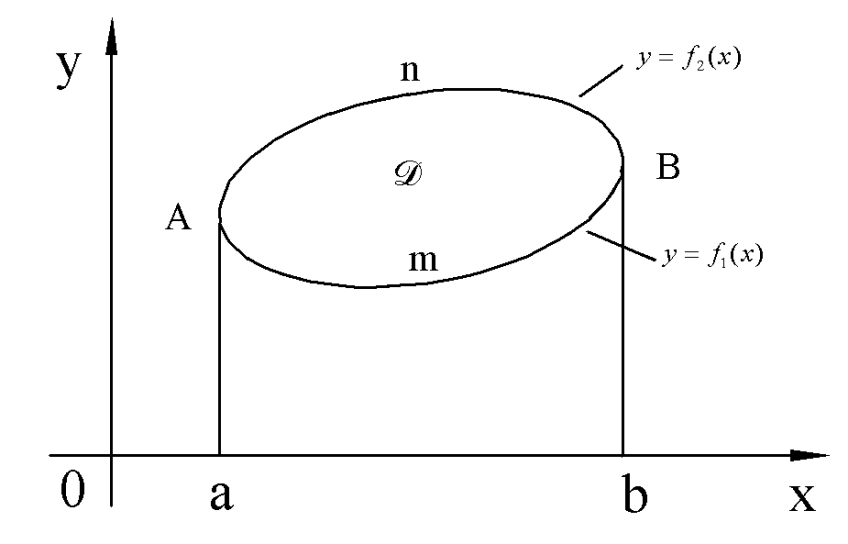
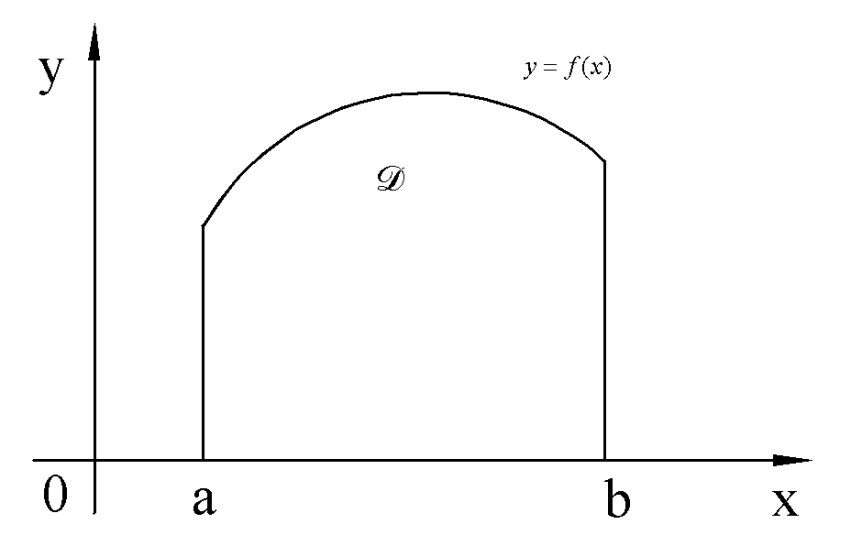
Пусть на плоскости задана ограниченная область D.
Область D проецируется на ось ОХ в отрезок 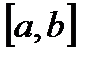 . Будем предполагать, что любая прямая
. Будем предполагать, что любая прямая 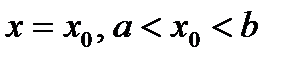 , пересекает границу области D в двух точках. Прямые
, пересекает границу области D в двух точках. Прямые 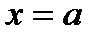 и
и 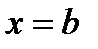 могут иметь с границей области общие отрезки.
могут иметь с границей области общие отрезки.
В данном случае можно записать уравнение кривой, ограничивающей область D снизу 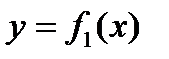 и уравнение кривой, ограничивающей область D сверху
и уравнение кривой, ограничивающей область D сверху 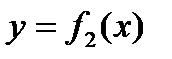 .
.
Отрезок [a,b] произвольным способом разобьем на n частей точками 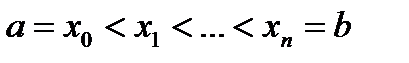 . Это разбиение обозначим через Т. Через
. Это разбиение обозначим через Т. Через 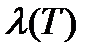 обозначим наибольшую из длин частей разбиения. Пусть
обозначим наибольшую из длин частей разбиения. Пусть 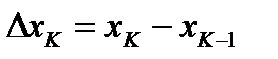 , тогда
, тогда 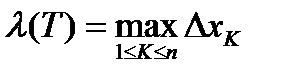 .
.
В каждой из частей разбиения произвольным способом выберем по точке 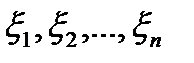 .
.
Прямые 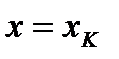 разобьют область D на n частей. К-тую часть разбиения заменим прямоугольником с основанием
разобьют область D на n частей. К-тую часть разбиения заменим прямоугольником с основанием 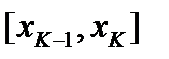 и высотой
и высотой 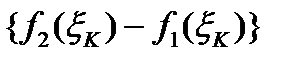 .
.
Площадь S фигуры D приближенно равна 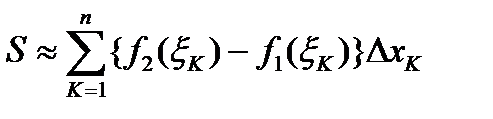 .
.
Определение. Площадью S области D называется 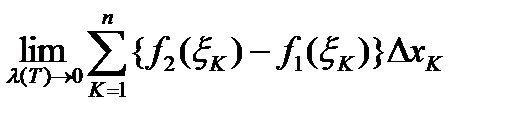 , если предел существует. Если данный предел не существует, то область D площади не имеет. Если область D имеет площадь, то она называется квадрируемой.
, если предел существует. Если данный предел не существует, то область D площади не имеет. Если область D имеет площадь, то она называется квадрируемой.
В определении площади области D сумма, стоящая под знаком предела является интегральной суммой для функции 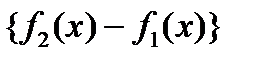 , поэтому
, поэтому  и
и
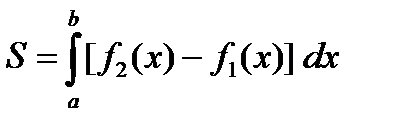 .
.
Если 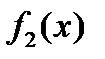 и
и 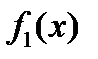 непрерывные функции на отрезке
непрерывные функции на отрезке 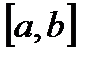 , то по теореме существования определенного интеграла можно утверждать, что область D имеет площадь, т.е. область D квадратируема.
, то по теореме существования определенного интеграла можно утверждать, что область D имеет площадь, т.е. область D квадратируема.
Замечание 1. Область D можно проецировать на ось OY на отрезок 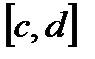 и тогда
и тогда 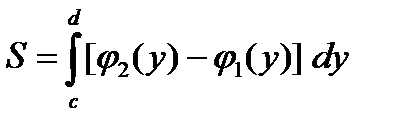 , где кривая
, где кривая 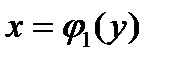 ограничивает область D снизу, а кривая
ограничивает область D снизу, а кривая 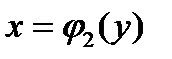 ограничивает область D сверху.
ограничивает область D сверху.
Замечание 2. Если область D такова, что сразу нельзя по предыдущим формулам вычислить площадь в области D, то область D надо разбить на конечное число частей, не имеющих общих внутренних точек, так что можно вычислить площадь каждой из частей. Тогда площадь в области D вычислится как сумма площадей частей разбиения.
Пример. Вычислить площадь фигуры, ограниченной линиями 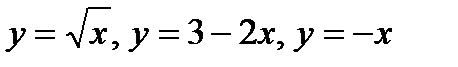 .
.
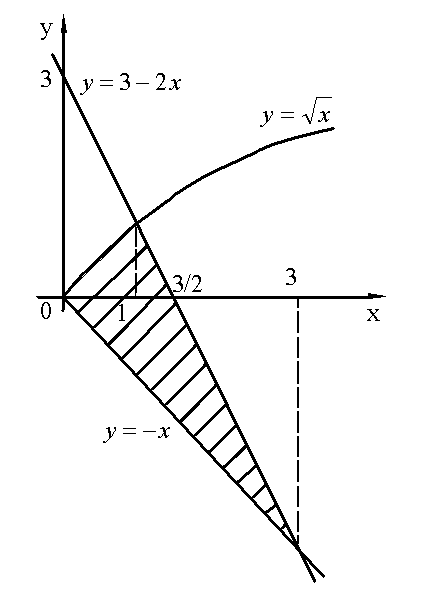
Область D проецируется на ось OX в отрезок [0,3]. Сверху область D ограничена линией 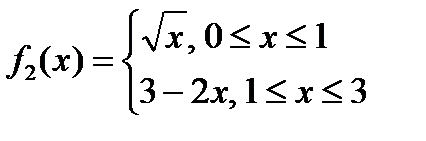
Снизу область D ограничена линией 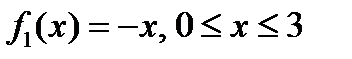 . По формуле находим:
. По формуле находим: 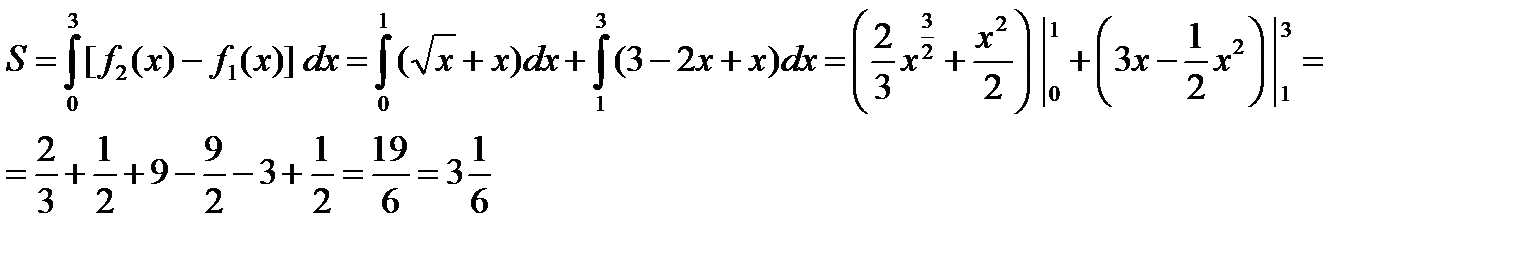
8.1.2. Вычисление площади фигуры, граница которой задана параметрически.
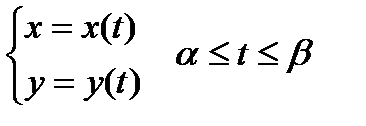
Пусть область D проецируется на ось OX в отрезок [a,b] и 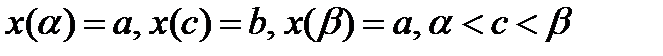 . Функция x=x(t) на промежутках
. Функция x=x(t) на промежутках 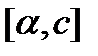 и
и 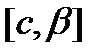 монотонна и имеет непрерывную производную.
монотонна и имеет непрерывную производную.
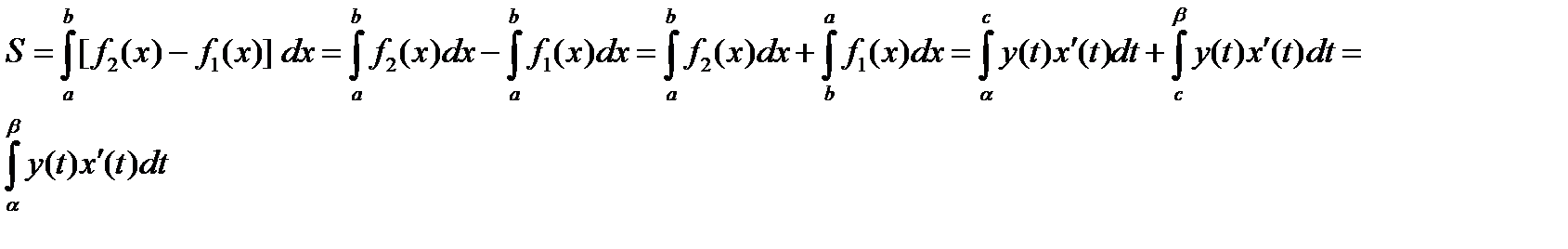 В частности, если требуется вычислить площадь криволинейной трапеции, причем уравнение верхней кривой
В частности, если требуется вычислить площадь криволинейной трапеции, причем уравнение верхней кривой 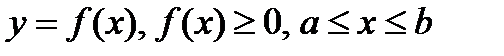 , задано параметрически
, задано параметрически
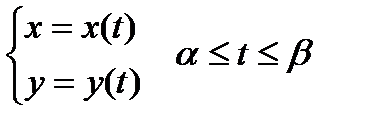 , где x(t) монотонная функция имеет непрерывную производную на
, где x(t) монотонная функция имеет непрерывную производную на 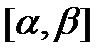 ,
, 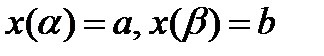 , то где
, то где 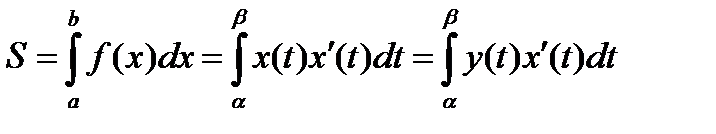 .
.
Пример. Вычислить площадь фигуры, ограниченной осью ОХ и одной аркой циклоиды
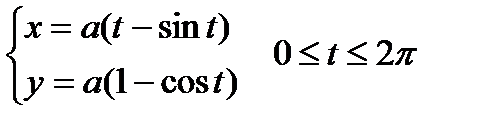
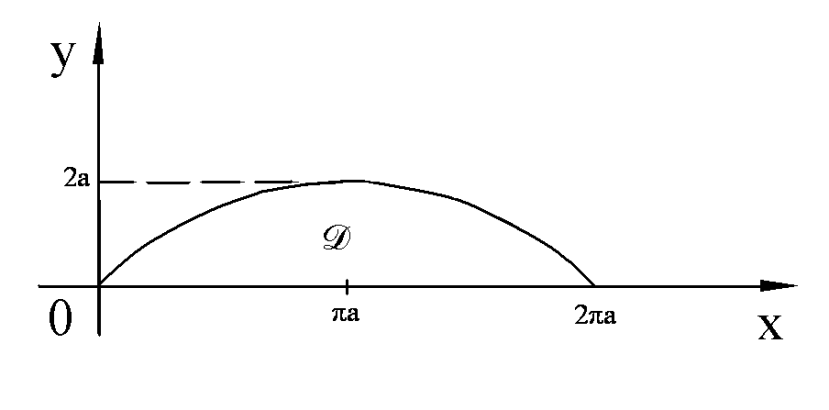
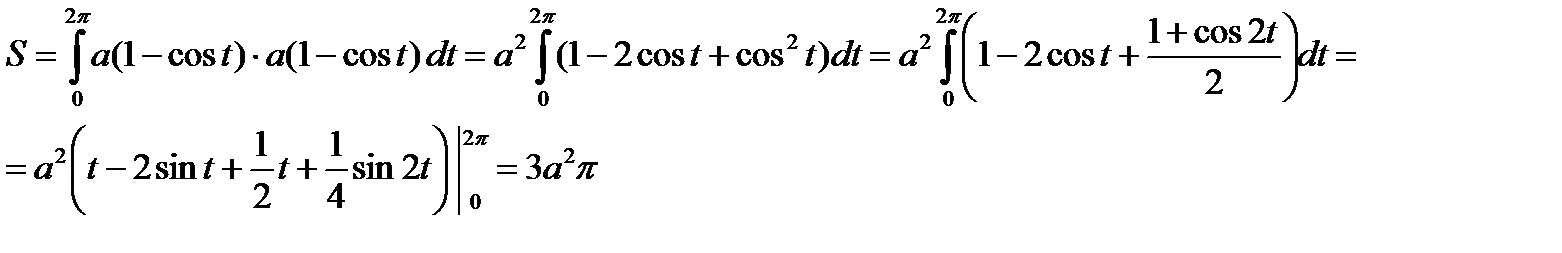
Пример. Вычислить площадь фигуры, ограниченной эллипсом 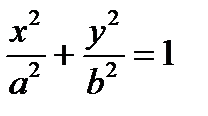 . Запишем уравнение эллипса в параметрическом виде: x=acost, y=bsint,
. Запишем уравнение эллипса в параметрическом виде: x=acost, y=bsint, 
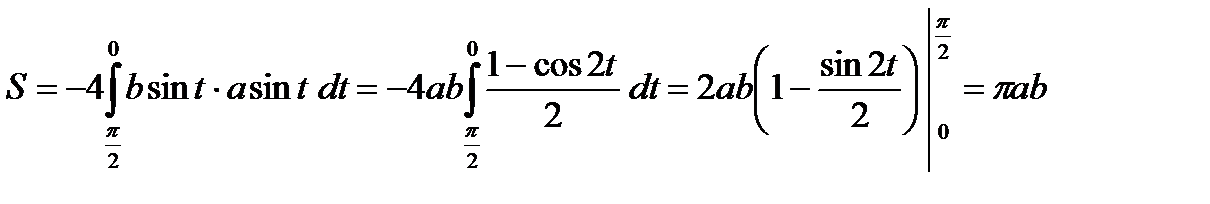 .
.
8.1.3. Вычисление площади фигуры в полярной системе координат.
Вычислим теперь площадь области D в полярной системе координат.
Пусть область D ограничена лучами 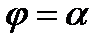 и
и 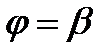 . Будем предполагать, что любой луч
. Будем предполагать, что любой луч 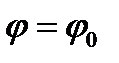 ,
, 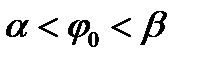 , пересекает границу области D в двух точках. В этом случае область D будет ограничена двумя линиями
, пересекает границу области D в двух точках. В этом случае область D будет ограничена двумя линиями 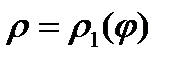 ,
, 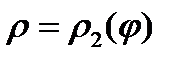 и лучами
и лучами 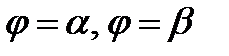 .
.
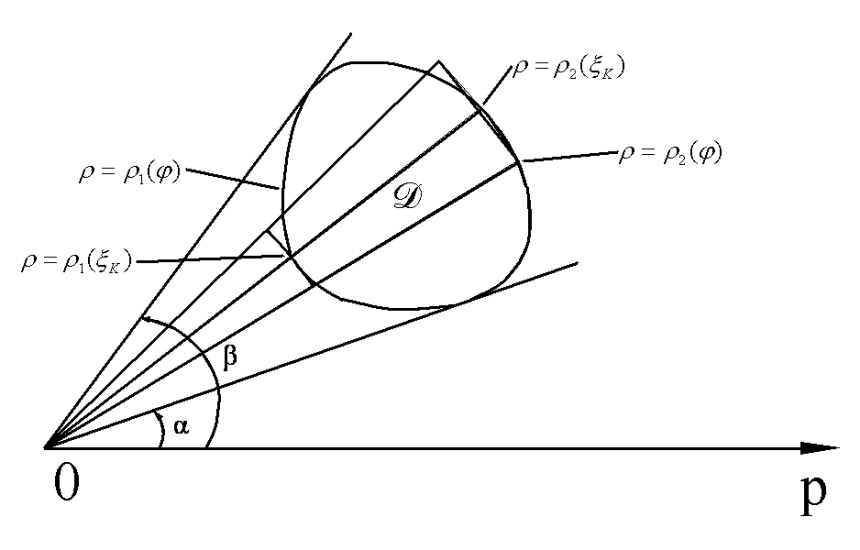
Угол между лучами 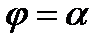 и
и 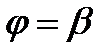 разобьем произвольным способом на n частей лучами
разобьем произвольным способом на n частей лучами 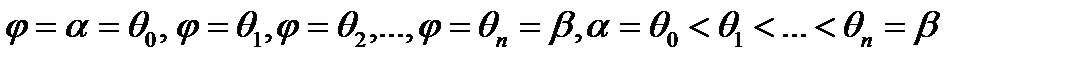 .
.
Это разбиение обозначим через (Т), 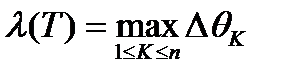 , где
, где 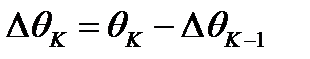 .
.
В каждом частичном угле выберем произвольным способом луч 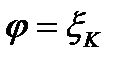 .
.
К-тому углу поставим в соответствие два круговых сектора с радиусами 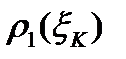 и
и 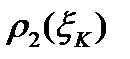 .
.
Площадь области D приближенно равна
 .
.
Естественно за S принять предел таких сумм при 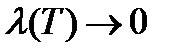 .
.
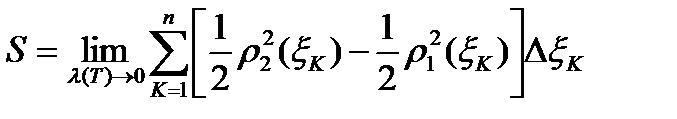
Выражение, стоящее под знаком предела, является интегральной суммой для функции 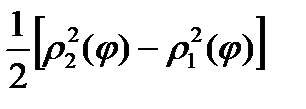 .
.
Следовательно,
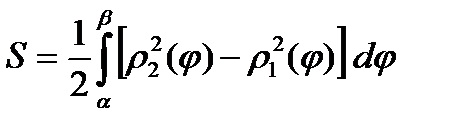 .
.
Рассмотрим два частных случая.
1) Пусть полюс 0 лежит на границе области D. В этом случае 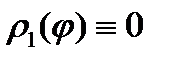 , а
, а 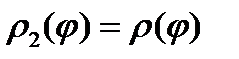 .
.
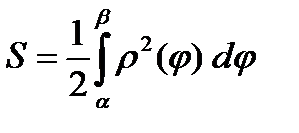
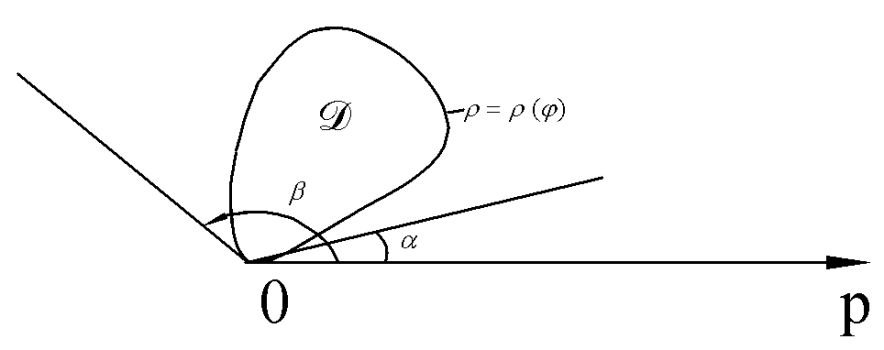
2) Пусть полюс 0 лежит внутри области D
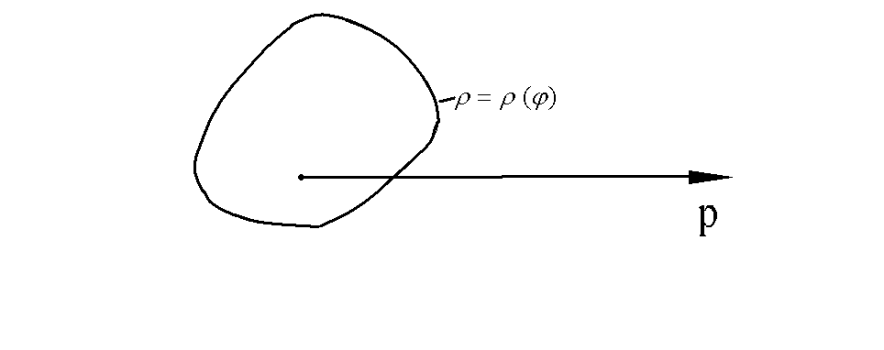
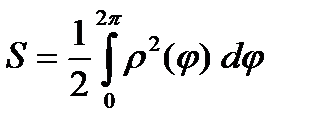
Пример. Вычислить площадь фигуры, ограниченной кардиоидой 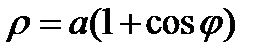
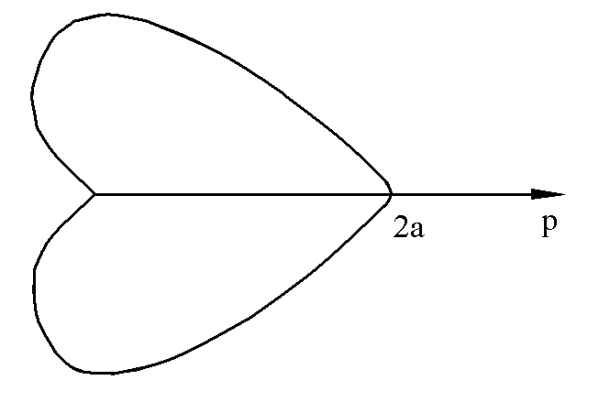
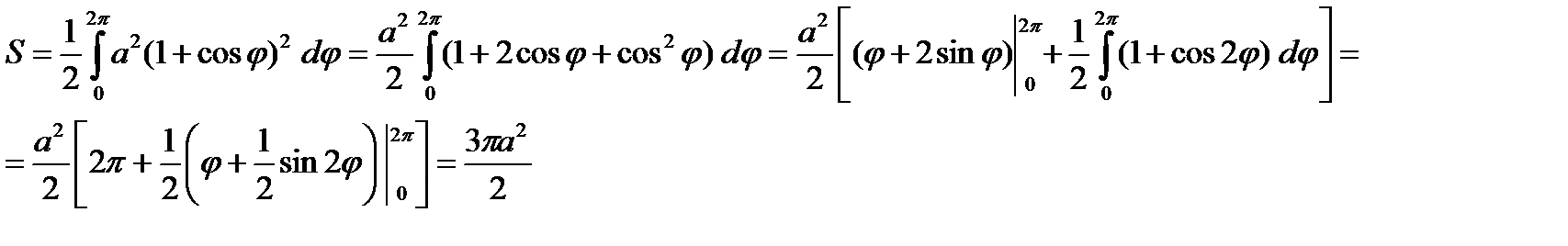
8.2. Вычисление объемов тел.
Общее определение объема тела связано с изучением двойного интеграла и будет изложено в III семестре. Сейчас мы рассмотрим некоторые частные случаи.
8.2.1. Вычисление объемов тел по площадям параллельных сечений.
Пусть в пространстве дано ограниченное тело, границей которого является замкнутая поверхность.
Данная область проецируется на ось ОХ в отрезок 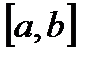 . Будем предполагать, что
. Будем предполагать, что 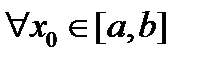 известна площадь
известна площадь 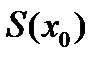 сечения данного тела плоскостью
сечения данного тела плоскостью 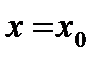 .
.
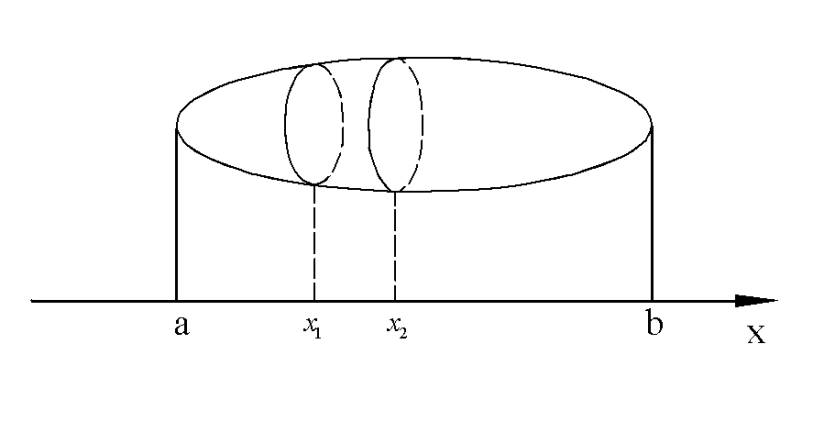
Отрезок 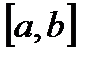 произвольным способом разобьем на n частей точками
произвольным способом разобьем на n частей точками 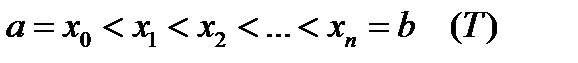 . Пусть
. Пусть 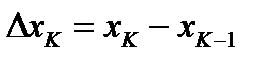 ,
, 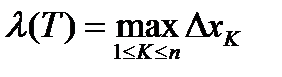 .
.
Плоскости 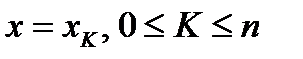 разобьют данное тело на n частей.
разобьют данное тело на n частей.
В каждом из отрезков разбиения 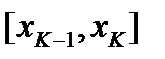 произвольным способом выберем по точке
произвольным способом выберем по точке 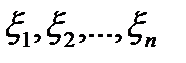 .
.
Объем К-той части разбиения данного тела приближенно равен 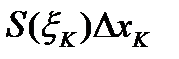 , а объем всего тела приближенно равен
, а объем всего тела приближенно равен
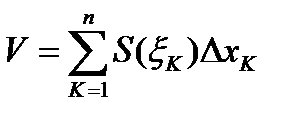 .
.
За объем тела принимают предел сумм 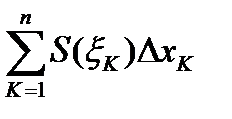 при
при 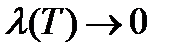 , т.е.
, т.е.
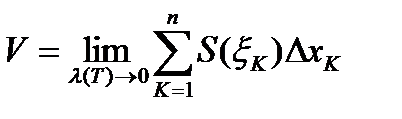 .
.
Сумма, стоящая под знаком предела, является интегральной суммой для функции s(x), поэтому
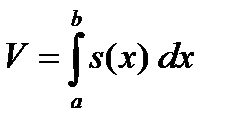 .
.
Отметим, что мы дали определение объема тела и указали способ его вычисления.
Пример. Вычислить объем тела, ограниченного эллипсоидом 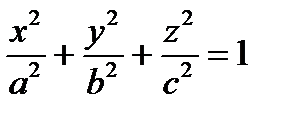 .
.
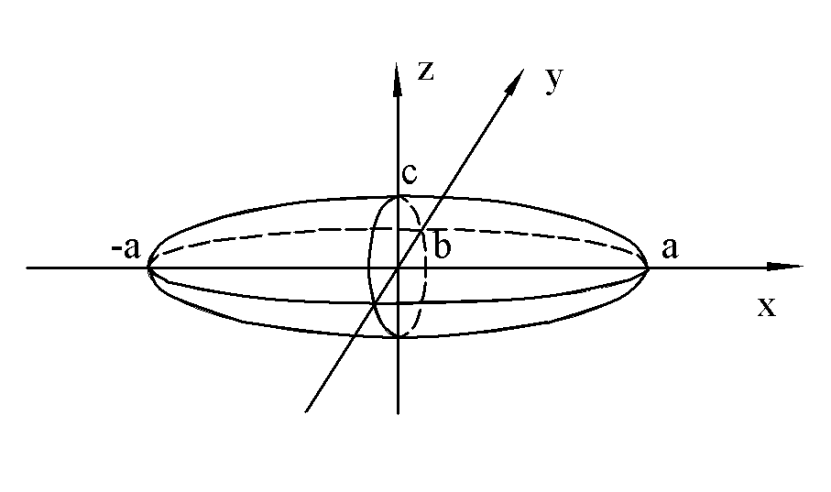
Данный эллипсоид проецируется на ось OX в отрезок 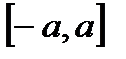 .
.  плоскость
плоскость 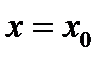 пересекает тело по области, границей которой является эллипс
пересекает тело по области, границей которой является эллипс 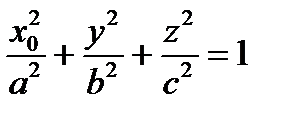 . Найдем полуоси этого эллипса
. Найдем полуоси этого эллипса 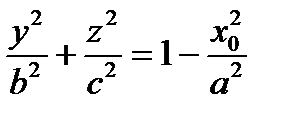 ;
; 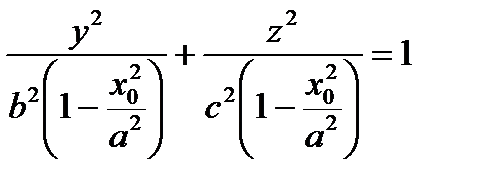 .
.
Следовательно, полуосями эллипса являются 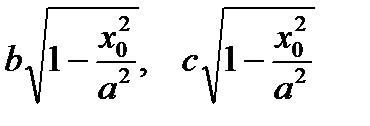
Поэтому, площадь сечения 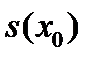 равна
равна
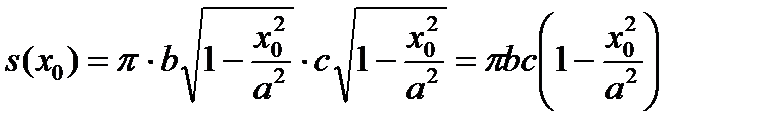 .
.
Объем тела вычисляется по формуле
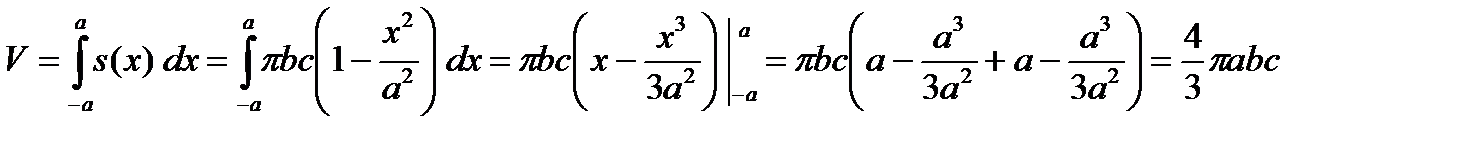 .
.
Если a=b=c, то тело, ограниченное эллипсоидом, является шаром.
 , где a – радиус шара.
, где a – радиус шара.
8.2.2. Вычисление объемов тел вращения.
Пусть тело является телом вращения криволинейной трапеции вокруг оси OX.
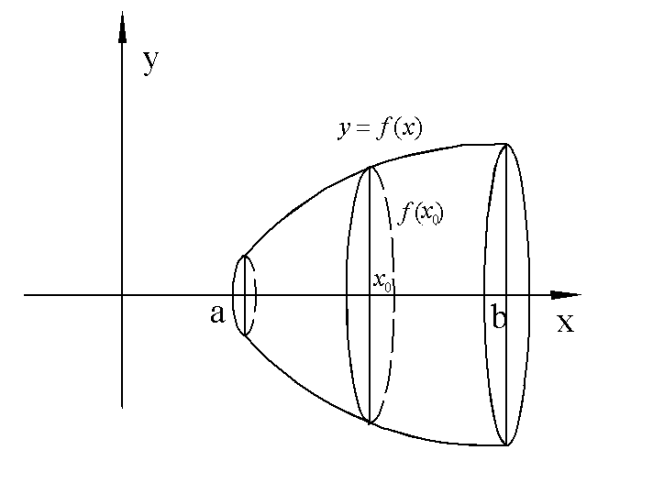
В этом случае 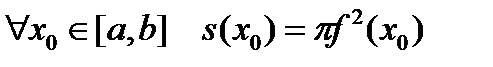 и
и 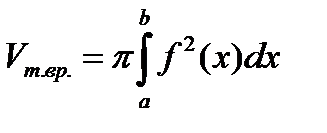 .
.
Пусть теперь тело является телом вращения фигуры D, которая не пересекает оси OX, причем любая прямая, параллельная оси OY пересекает границу D не более чем в двух точках.
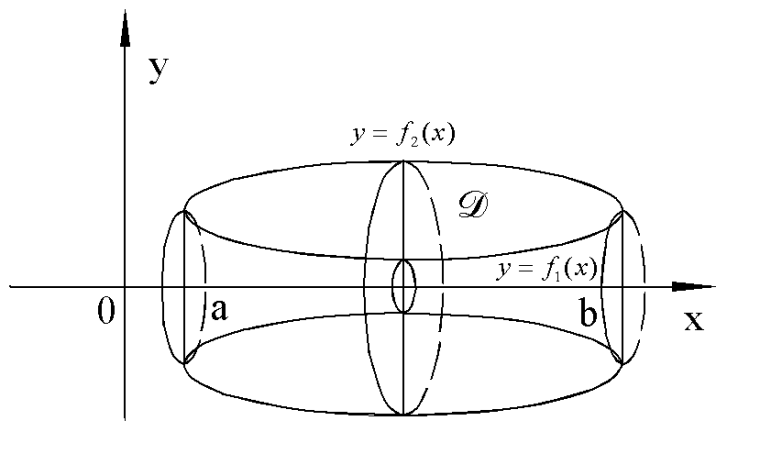
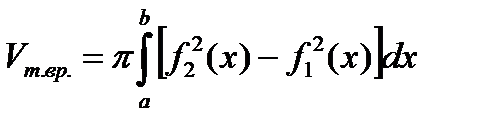 .
.
Пример. Вычислить объем тела вращения круга 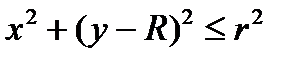 ,
, 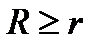 , вокруг оси OX.
, вокруг оси OX.
Такое тело называется тором.
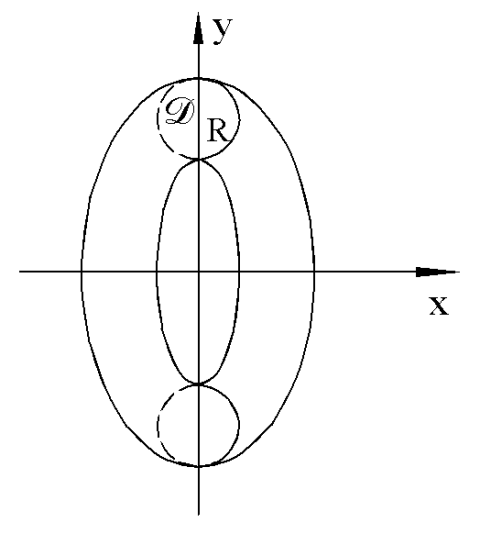
Фигура D ограничена сверху полуокружностью 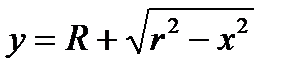 , а снизу полуокружностью
, а снизу полуокружностью  . Поэтому
. Поэтому

Последний интеграл есть площадь половины круга радиуса r. Поэтому 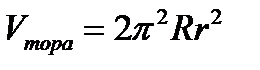 .
.
Дата добавления: 2015-08-21; просмотров: 2404;
