Теорема Коши

Дифференциальные уравнения 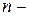го порядка записывается:

в явном виде

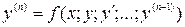, (3)

в неявном виде

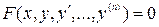
Задача Коши. Найти решение уравнения (3), удовлетворяющее начальным данным: при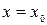

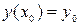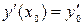, , … , (4)

Теорема Коши. Если в некоторой замкнутой области 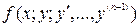непрерывна по всем аргументам и имеет в этой области ограниченные частные производные 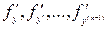, то уравнение (3) имеет единственное решение, удовлетворяющее начальным данным (4), где 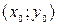принадлежит этой области.

1.3 Общее и частные решения

Функция

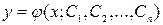(5)

Где 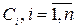- произвольные постоянные, называется общим решение уравнения (3), если:

а) она является решением уравнения (3) при любом конкретном наборе ,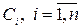

б) при любых начальных данных в области, где выполняются условия теоремы Коши, можно подобрать конкретный набор 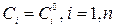так, что

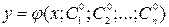(6)

Удовлетворяет начальным данным.

Решение (6) называется частным решением. Геометрически (5) – семейство кривых (интегральные кривые). Выполнение условий теоремы Коши означает, что через т. 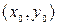проходит только одна интегральная кривая, удовлетворяющая условиям (4). Общее (частное) решение уравнения (3) заданное в неявном виде

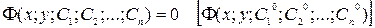называется общим (частным) интегралом.

Кроме общего и частного решения уравнение (3) может иметь особые решения: решения уравнения (№), не получающееся из общего ни при каком конкретном наборе .

Пример 3. Рассмотрим уравнение

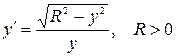(7)

Непосредственной подстановкой можно проверить, что

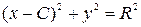(8)

общий интеграл уравнения (7). Так как

,

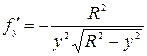то на прямых 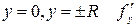- неограниченна, т.е. нарушено условие теоремы Коши. Очевидно, что 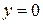не является решением (7), а прямые - решения (7), не получающиеся из (8) ни при каком конкретном значении . Геометрически это означает, что через любую точку прямых проходят две интегральные кривые: например через т. 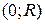проходят интегральные кривые 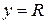и 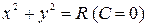. Следовательно особые решения.

Как видно из примера 2 при решении уравнения, мы находим первообразные. Поэтому процесс нахождения решения дифференциального уравнения называется интегрированием уравнения.

Выводы:

1) дифференциальное уравнение (ДУ) имеет бесчисленно много решений;

2) общее решение ДУ зависит от произвольных постоянных, число которых равно порядку ДУ;

3) частные решения ДУ получаются из общего путем придания конкретных значений этим постоянным.