Линейные уравнения

Определение 3. Дифференциальное уравнение, содержащее искомую функцию и ее производные только в первой степени, называется линейным.

Линейные уравнения 1-го порядка

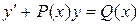(3)

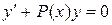, (4)

Называются: (3) – неоднородное, (4) – однородное.

Найдем общее решение однородного уравнения

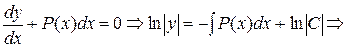
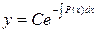(5)

Методом Лагранжа (вариации произвольной постоянной) найдем решение уравнения (3). Решение ищем в виде (5), где 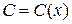- неизвестная функция (варьируем). Подставляя в (3) вместо .

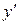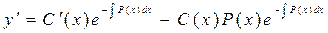
а вместо 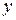- (5), получим

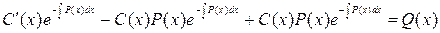
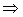
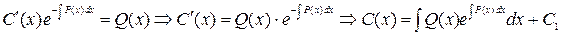
Подставляя 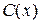в (5), получим общее решение (3).

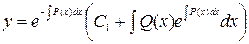(6).

З а м е ч а н и е 4. Так как 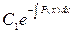- общее решение (4), а 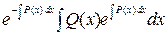- частное решение (при 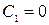) уравнения (3), то можно сделать вывод П части щимися перменными. Делимавнениям с разделяющимимся переменными подстановкой?, верный для линейных уравнений любого порядка: общее решение линейного неоднородного уравнения есть сумма общего решение линейного неоднородного уравнения и частного решения неоднородного.

Пример 5. Решить уравнение .

Уравнение не является линейным относительно 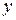. Если положим 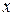- функция от 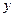, затем полагая , получим

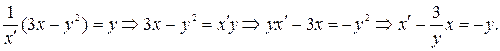
Это уравнение относительно 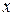линейное, .

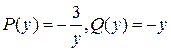Из (6)

.

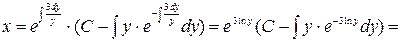
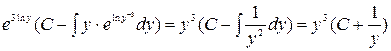
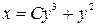Пример из экономики. Уравнение Самуэльсона. Паутинная модель рынка

Рассмотрим уравнение Самуэльсона

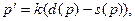
моделирующее связь между изменением цены 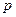и неудовлетворенным спросом 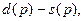где 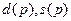- соответственно величины спроса и предложения при цене 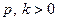. Предположим, что спрос и предложение задаются линейными функциями

,

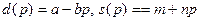где - некоторые положительные числа.

С учетом этого, ДУ примет вид:

.

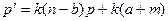Это уравнение является линейным неоднородным ДУ и решается по формуле (6), применив которую получим общее:

.

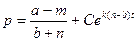Эта зависимость показывает, что при 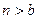с течением времени функция 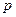будет отделяться от состояния равновесия . Если же 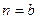, то 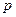- постоянна, а если 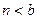, то с течением времени 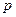будет асимптотически приближаться к состоянию равновесия . Данную модель рассматривают как непрерывный аналог паутинной модели рынка.