Уравнение в полных дифференциалах

Определение 2.Если существует функция 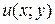, полный дифференциал которой в некоторой области равен левой части (10), то (10) – уравнение в полных дифференциалах.

Таким образом

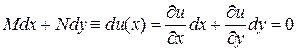(17)

Теорема. Пусть 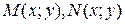непрерывны и дифференцируемы, причем 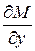и 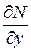- непрерывны в некоторой области. Для того, чтобы уравнение (10) являлось уравнением в полных дифференциалах необходимо и достаточно, чтобы

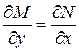(18)

причем общий интеграл записывается.

,

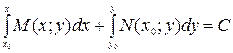Где 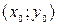любая точка, в окрестности которой существует решение (10).

Пример 7. Проинтегрировать ДУ вида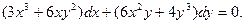

Решение. Так как 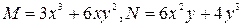и 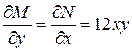, то уравнение в полных дифференциалах. Пусть 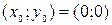. Тогда

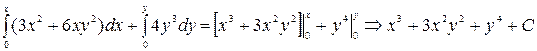
Литература

1. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. М.: Наука, 1985г.
2. Краснов М.Л. Обыкновенные дифференциальные уравнения. М.: Высшая школа 1983г.
3. Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. Т.1,2 М.: Наука, 1985г.
4. Сборник индивидуальных заданий по высшей математике ч.1-3 Под редакцией Рябушко А.П. Минск.: Вышейшая школа, 2001 г.
5. Данко П.Е., Попов А.Г., Кожевников Т.Я. Высшая математика в упражнениях и задачах. Ч.1,2 М.: Высшая школа,1986 г.
6. Кузнецов Л.А. Сборник заданий по высшей математике (типовые расчеты). М.: Высшая школа, 1983 г.