Математические модели экономического роста

Определение 1.Уравнение, вида

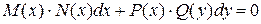, (1)

коэффициенты которого пр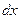и и 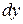- произведение функции только от 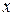на функцию только от 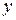, называется уравнением с разделяющимися переменными.

Считая, что 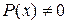, , делим обе части (11) на

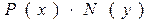
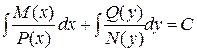
З а м е ч а н и е 1. Случай 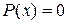, 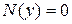исследуется дополнительно.

Пример 1. Решить уравнение

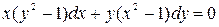
Решение. Это уравнение с разделяющимися переменными. Разделим на 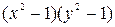, считая , что .

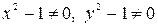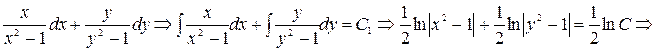
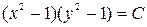- (2)

общий интеграл. Рассмотрим теперь 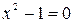и .

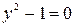Получим решения уравнения (легко проверить непосредственной подстановкой в уравнение) 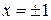и 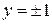. Но эти же решения получаются из (12) при 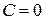. Следовательно ответ: .

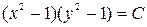З а м е ч а н и е 2. Частный случай уравнения (1).

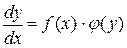
Пример 2. Найти функцию, имеющую постоянную эластичность, равную к.

Решение. По определению эластичность функции равна 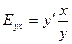, тогда по условию задачи получим: 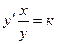дифференциальное уравнение с разделяющимися производными:

.

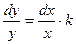Интегрируя обе части полученного равенства, находим:

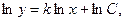
Откуда следует, что .

Пример из экономики. Построить модель естественного роста ( рост при постоянном темпе).

Решение:обозначим 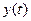- интенсивность выхода продукции некоторого предприятия (отрасли). Мы будем предполагать, что имеет место аксиома о ненасыщенности потребителя, т.е. что весь выпущенный товар будет продан, а также то, что объем продаж не является столь высоким, чтобы существенно повлиять на цену товара 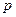, которую будем считать фиксированной. Чтобы увеличить интенсивность выпуска 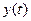, необходимо, чтобы чистые инвестиции 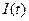(т.е. разность между общим объемом инвестиции и амортизированными затратами) были больше нуля. В случае 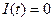общие инвестиции только лишь покрывают затраты на амортизацию, и уровень выпуска продукции остается неизменным. Случай 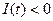приводит к уменьшению основных фондов и, как следствие, к уменьшению уровня выпуска продукции. Таким образом, скорость увеличении интенсивности выпуска продукции является возрастающей функцией от .

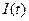Пусть эта зависимость выражается прямой пропорциональностью, т.е. имеет место так называемый принцип акселерации

,

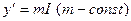где 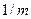- норма акселерации. Пусть 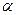- норма чистых инвестиций, т.е. часть дохода 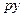, которая тратится на чистые инвестиции, тогда 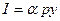. Обозначая , окончательно получим ДУ:

.

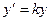Интегрируя данное ДУ с разделяющимися переменными, найдем общее его решение:

.

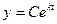При начальном условии 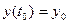, найдем частное решение .

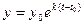Это решение называется уравнением естественного роста. Оно описывает динамику роста цен при постоянном темпе инфляции.