Однородное дифференциальное уравнение

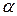Определение 2. Функция называется однородной порядка относительно 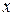и 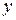, если для любого : .

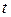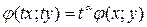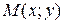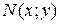Если и - однородные функции одного порядка, то (10) однородное уравнение. Уравнение 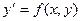будет однородным, если 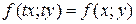, т.е. .

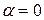Однородные уравнения сводятся к уравнениям с разделяющимися переменными подстановкой:

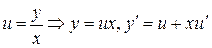или .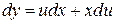

Пример 4. Решить уравнение .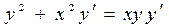

Приведем к виду (10).

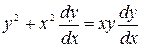
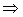
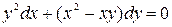
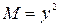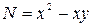Так как и - однородные функции порядка 2, то уравнение однородное. Делаем подстановку .

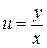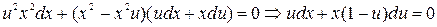- уравнение С разделяющимися переменными. Делим обе части на 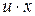. Получим

.

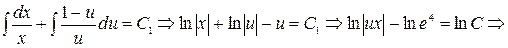
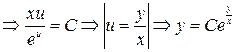Случа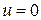й и 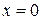равносилен 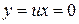. Получается при С=0.

З а м е ч а н и е 3. Уравнения вида

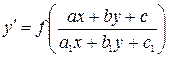
Приводятся к однородным.