Экономическая задача, приводящая к дифференциальному уравнению
Лекция 3-4
Обыкновенные дифференциальные уравнения
Общее и частные решения. Уравнения первого порядка. Уравнения с разделяющимися переменными. Однородные уравнения.
Линейные дифференциальные уравнения. Уравнение Бернулли.
Уравнений в полных дифференциалах.
Вопросы
1. Определение обыкновенных дифференциальных уравнений.
2. Дифференциальные уравнения первого порядка.
3. Общее решение дифференциального уравнения.
4. Задачи Коши. Частное решение.
5.Определение дифференциального уравнения 1-ого порядка.
6. Дифференциальные уравнения с разделяющимися переменными.
7. Однородные дифференциальные уравнения.
8. Линейные дифференциальные уравнения первого порядка.
9.Уравнение Бернулли.
10.Уравнение в полных дифференциалах
Различные вопросы экономики приводят к необходимости решения уравнений, содержащей в качестве неизвестной некоторую функцию и ее производные до определенного порядка n.
Экономическая задача, приводящая к дифференциальному уравнению
Обозначим 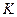 - величина фондов в натуральном или стоимостном выражении. Фонды – это станки, помещения и т.п. они изнашиваются, стареют, как говорят, выбывают. Скорость выбытия фондов – это производная
- величина фондов в натуральном или стоимостном выражении. Фонды – это станки, помещения и т.п. они изнашиваются, стареют, как говорят, выбывают. Скорость выбытия фондов – это производная 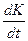 , она выражается через коэффициент выбытия
, она выражается через коэффициент выбытия  . Например, если за 10 лет фонды полностью обновляются, то коэффициент выбытия равен
. Например, если за 10 лет фонды полностью обновляются, то коэффициент выбытия равен  =1/10. С другой стороны, инвестиции
=1/10. С другой стороны, инвестиции 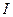 – вложение денег – ведут к увеличению фондов с коэффициентом пропорциональности
– вложение денег – ведут к увеличению фондов с коэффициентом пропорциональности 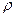 . Учитывая все это, получим дифференциальное уравнение, вида:
. Учитывая все это, получим дифференциальное уравнение, вида:
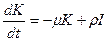 .
.
Дата добавления: 2015-08-21; просмотров: 1460;
