Тип 7: В теме растворы: задачи на нахождение массовой доли растворенного вещества.
Здесь можно выделить несколько подтипов задач:
- Нахождение массовой доли вещества, если известны массы вещества и воды.
- Нахождение массы растворенного вещества по известной массовой доле и массе раствора.
- Задачи на разбавление.
- Приготовление раствора с меньшей массовой долей из раствора с большей массовой долей.
- Приготовление раствора с большей массовой долей из раствора с меньшей массовой долей.
Все эти задачи решаются на основе одной математической формулы:
 .
.
Рассмотрим три последние подтипа задач.
1. Задачи на разбавление. При решении данных задач необходимо объяснить, что при добавлении к раствору воды массовая доля раствора меняется, так как меняется масса раствора, масса же растворенного вещества остается той же, что и была в исходном растворе.
Задача: К раствору массой 200 г с массовой долей соли 15% добавили 100 мл воды. Найти массовую долю соли во вновь полученном растворе.
| Дано: | |
| w исх. (р-ра) = 15% | |
| m исх. (р-ра) = 200 г | |
| V(H2O) = 100 мл | |
| w2 = ? |
Решение:
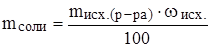
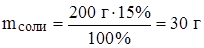
m(H2O) = V ·r m(H2O) = 100 г
m2 (р-ра) = mисх.(р-ра) + M(H2O) m2 (р-ра) = 200 г + 100 г = 300 г
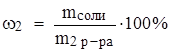

2. Задачи на приготовление раствора с меньшей массовой долей из раствора с большей массовой долей. Эти задачи лучше всего решать, начиная с того раствора, который надо приготовить:
а) найти, какая масса чистого вещества необходима для приготовления заданного раствора;
б) найти, в какой массе исходного раствора содержится нужная масса чистого вещества;
в) перейти, если нужно, от массы к объему.
Задача: Какой объем 96%‑ного раствора серной кислоты (r = 1.84 г/мл) потребуется для приготовления 200 г 25%‑ного раствора серной кислоты?
| Дано: | |
| w исх. = 96% (H2SO4) | |
| rисх. = 1.84 г/мл | |
| m2 (р-ра) = 200 г | |
| w2 (H2SO4) = 25% | |
| Vисх. р-ра = ? |
Решение:
а) 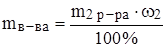
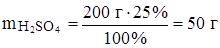
б) 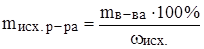
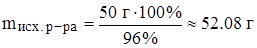
в) 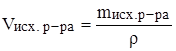
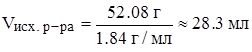 .
.
3. Задачи на приготовление раствора с большей массовой долей из раствора с меньшей массовой долей. При решении этих задач необходимо объяснить, что большая массовая доля получается при добавлении твердого вещества или раствора с большей массовой долей. Таким образом, меняются и масса раствора, и масса вещества. Такие задачи лучше решать алгебраическим способом.
Задача: Какую массу NaCl надо добавить к 300 г 10%‑ного раствора, чтобы получить 20%‑ный раствор этой соли?
| Дано: | |
| m исх. (р-ра) = 300 г | |
| w исх. (NaCl) = 10% | |
| w2 (NaCl) = 20% | |
| m(NaCl) = ? |
Решение (способ 1):
Обозначим искомую массу NaCl через x:
m(NaCl) = x.
Найдем массу NaCl в исходном растворе:
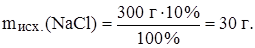
Выразим w(NaCl) в новом растворе:
m2(NaCl) = 30 г + х.
m2(р-ра) = 300 г + х, то есть m2(р-ра) = mисх.(р-ра) + х.
Используя формулу:
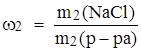 ,
,
составляем уравнение:
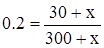 , 0.2 · (300 + х) = 30 + х,
, 0.2 · (300 + х) = 30 + х,
60 + 0.2 х = 30 + х, 30 = 0.8 х, х = 37.5, m(NaCl) = 37.5 г.
Решение (способ 2): 20%‑ный раствор – это 20 г NaCl на 80 г H2O. Найдем массу H2O в исходном растворе:
m(H2O) = mисх.(р-ра) – m(NaCl) = 300 г – 30 г = 270 г.
20 г NaCl - 80 г H2O
x г NaCl - 270 г H2O,
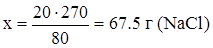 ,
,
m(NaCl) = 67.5 г – 30 г = 37.5 г.
Правило креста используется при смешивании двух растворов с разными массовыми долями вещества:
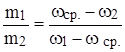 , где wср. – массовая доля вещества в растворе, получающемся после смешивания растворов с массовыми долями вещества w1 и w2.
, где wср. – массовая доля вещества в растворе, получающемся после смешивания растворов с массовыми долями вещества w1 и w2.
Для получения этой пропорции подписывают друг под другом величины массовых долей исходных растворов. Затем рисуют крест, исходящий из этих величин. В середине креста пишут величину массовой доли, которая получится после смешивания растворов. На оставшихся концах креста пишут величину, равную разности wср.‑ wi. Полученные величины дают соотношение масс исходных растворов.
Задача: Какую массу 40%‑ного раствора соли надо добавить к 10%‑ному раствору массой 20 г, чтобы получить 30%‑ный раствор?
| Дано: | |
| w1 = 40% | |
| w2 = 10% | |
| m2 = 20 г | |
| wср. = 30% | |
| m1 = ? |
Решение:
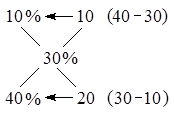
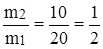 , таким образом, m1 = 2m2, m1 = 20 г · 2 = 40 г.
, таким образом, m1 = 2m2, m1 = 20 г · 2 = 40 г.
Дата добавления: 2015-08-21; просмотров: 2694;
