Статистический критерий проверки гипотез
Статистическим критерием K называют случайную величину, с помощью которой принимают решение о принятии или отклонении Н0.
Замечание. Для проверки параметрических гипотез используют критерии значимости, основанные на статистиках: u, χ2, t, F (приложения 5-7). Непараметрические гипотезы проверяют с помощью критериев согласия, использующих статистики распределений: 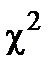 , Колмогорова-Смирнова [1, 2, 6, 10] и т.д.
, Колмогорова-Смирнова [1, 2, 6, 10] и т.д.
Например, Н0: М(х)=10. В зависимости от альтернативной гипотезы рассматривают три случая.
1. Если 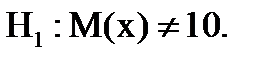
| f(K/H0) |
| K |
| Критическая область |
| Область принятия гипотезы Н0 |
| Ka/2 |
| a/2 |
| Критическая область |
| a/2 |
| K1-a/2 |
Рис 27. Двусторонняя критическая область
В этом случае рассматривают двустороннюю критическую область и используют дифференциальную функцию f (K/H0), для определения соответствующих квантилей (границ области принятия гипотезы - левой (К1-a/2) и правой (Кa/2)). Площадь под криволинейной трапецией дифференциальной функции слева от К1-a/2 и справа от Кa/2 равна a/2.
Общая площадь ограниченная криволинейной трапецией дифференциальной функции, квантилями и осью абсцисс равна (1 - α) (рис. 27):
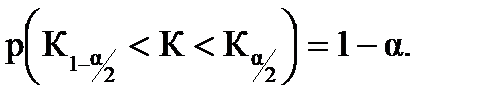 (11.1)
(11.1)
2. Если 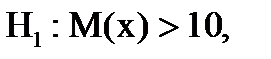 то рассматривается правосторонняя критическая область (площадь под криволинейной трапецией справа от Кa равна a) (рис. 28):
то рассматривается правосторонняя критическая область (площадь под криволинейной трапецией справа от Кa равна a) (рис. 28):
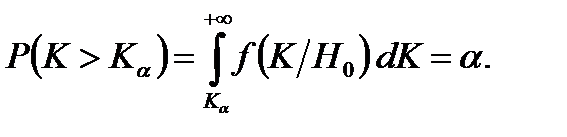 (11.2)
(11.2)
| f(K/H0) |
| K |
| Критическая область |
| Область принятия гипотезы Н0 |
| Ka |
| a |
Рис. Правосторонняя критическая область
3. Если 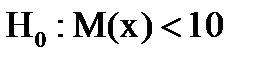 , то рассматривается левосторонняя критическая область (площадь под криволинейной трапецией слева от К1-a равна a) (рис. 29):
, то рассматривается левосторонняя критическая область (площадь под криволинейной трапецией слева от К1-a равна a) (рис. 29):
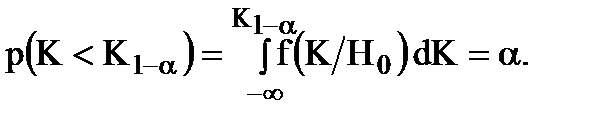 (11.3)
(11.3)
| f(K/H0) |
| K |
| Критическая область |
| Область принятия гипотезы Н0 |
| a |
| K1-a |
Рис. Левосторонняя критическая область
Алгоритм проверки статистических гипотез состоит из следующих этапов:
Располагая выборочными данными (  ), формируют нулевую гипотезу
), формируют нулевую гипотезу 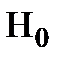 и конкурирующую гипотезу Н1.
и конкурирующую гипотезу Н1.
Задают уровень значимости α (обычно принимают α =0,1; 0,01; 0,05; 0,001).
Рассматривается выборочная статистика наблюдений (критерий) К, обычно одна из перечисленных ниже:
u - нормальное распределение;
χ2- распределение Пирсона (хи – квадрат);
t - распределение Стьюдента;
F - распределение Фишера - Снедекора.
4. На основании выборки 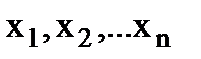 - определяют значение критерия (статистики) К (приложения 5-7). В зависимости от вида альтернативной гипотезы выбирают по соответствующей таблице квантили критерия для двусторонней
- определяют значение критерия (статистики) К (приложения 5-7). В зависимости от вида альтернативной гипотезы выбирают по соответствующей таблице квантили критерия для двусторонней 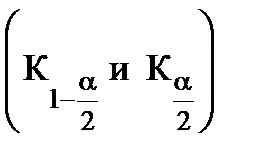 или односторонней области (К1-a или Кa) (приложения 1-4). Если значения критерия попадают в критическую область, то H0 отвергается; в противном случае принимается гипотеза H0 и считается, что Н0 не противоречит выборочным данным (при этом существует возможность ошибки с вероятностью равной a).
или односторонней области (К1-a или Кa) (приложения 1-4). Если значения критерия попадают в критическую область, то H0 отвергается; в противном случае принимается гипотеза H0 и считается, что Н0 не противоречит выборочным данным (при этом существует возможность ошибки с вероятностью равной a).
Следует отметить, что возможность принятия гипотезы происходит из принципа невозможности наступления маловероятных событий. Те же события, вероятность которых близка к 1, принимаются за достоверные. Возникает проблема выбора уровня риска (уровня значимости a).
В одних случаях возможно пренебрегать событиями р<0,05, в других нельзя пренебрегать событиями, которые могут появиться с р=0,001 (разрушение сооружений, транспортных средств и т.д.).
Дата добавления: 2015-08-11; просмотров: 716;
