Лекция 2.Проверка гипотез о равенстве средних. Критерии согласия.

Пусть требуется проверить нулевую гипотезу о нормальном законе распределения случайной величины. Уровень значимости принять a=0,001 .

Обычно точные параметры гипотети­ческого нормального закона нам неизвестны, поэтому нулевую гипо­тезу (Н₀) словесно можно сформулировать следующим образом: F(х) является функцией нормального распределения с параметрами М(X) =а = 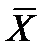и D(X) = .

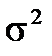Для проверки этой нулевой гипотезы найдем точечные оценки математического ожи­дания и среднего квадратического отклонения нормально распреде­ленной случайной величины:

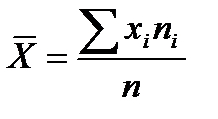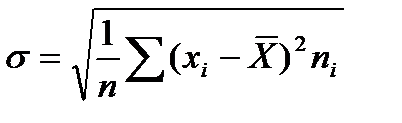: (11.4)

При проверке гипотезы о нормальном распределении генеральной совокупности сравниваются эмпирические (наблюдаемые) и теоретические (вычисленные в предположении нормальности распределения) частоты. Для этого используются статистика c² – Пирсона с n=k-r-1 степенями свободы (k – число групп, r – число оцениваемых параметров, в настоящем примере оценивались математическое ожидание и среднее квадратическое отклонение, следовательно, r = 2). Если c²_расч. ³ c²_кр., то нулевая гипотеза отвергается и считается, что предположение о нормальности распределения не согласуется с опытными данными. В противном случае (c²_расч. < c²_кр.) нулевая гипотеза принимается.

Вычисляются теоретические вероятности р_i, попадания СВ Х®N в частичные интервалы [x_i-1; x_i) по формуле:

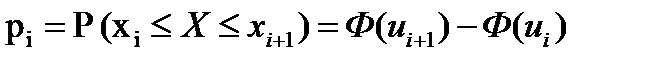, (i=1,2,...,k), (11.5)

где

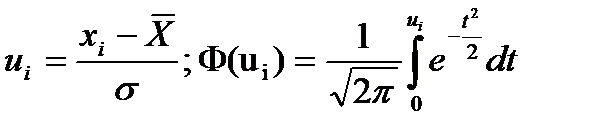. (11.6)

Применение критерия c², для проверки гипотезы о нормальности распределения предполагает наличие в каждом частичном интервале не менее пяти единиц, в противном случае желательно объединять эти интервалы с соседними.

Проверка гипотезы о принадлежности СВ показательному, биномиальному, пуассоновскому или другому распределению основывается на применении в описанном алгоритме соответствующих интегральных функций.

По таб­лице квантилей c²-распределения , при заданном уровне значимости a и числе степеней свободы n=k-r-1 находится критическое значение, которое сравнивается с фактически наблюдаемым значением. Если c²_расч.< c²_{кр. ,} то нет оснований для отклонения нулевой гипотезы о нормальном законе распределе­ния.

Пример. Из нормальной генеральной совокупности сельскохозяйственных предприятий, рассматриваемых по показателю урожайности пшеницы, с известным средним квадратическим отклонением s=9,4 и генеральной средней 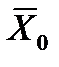=38,1, извлечена выборка объема n=50. По ней найдена выборочная средняя 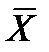=42. Требуется при уровне значимости a=0,05 проверить нулевую гипотезу Н₀:

а) 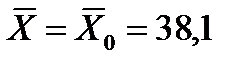, при конкурирующей гипотезе Н₁: 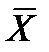¹38,1;

б) 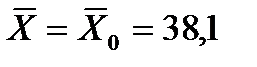, при конкурирующей гипотезе Н₁: 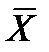<38,1;

в) 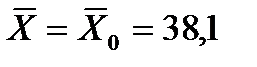, при конкурирующей гипотезе Н₁: 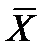>38,1.

Решение. Необходимо рассмотреть критерий К=u, где 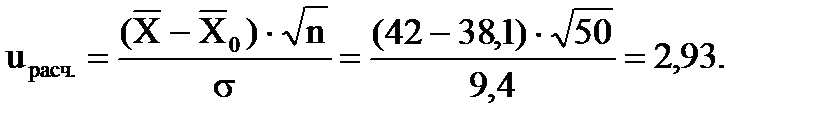(11.7)

а) По условию конкурирующая гипотеза имеет вид 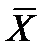¹38,1, поэтому критическая область двусторонняя. Найдем критическую точку из равенства Ф(u_кр.,a/2)=(1-a)/2=(1-0,05)/2=0,475. Согласно приложения 1: u_кр.=1,96.

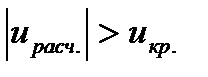, поэтому следует отклонить нулевую гипотезу, то есть выборочная и гипотетическая генеральная средняя статистически различаются значимо.

б) По условию конкурирующая гипотеза имеет вид 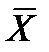<38,1, поэтому критическая область левосторонняя. Найдем критическую точку из равенства Ф(u_кр.,a)=(1-2a)/2=(1-0,1)/2=0,45. Согласно приложения 1: u_кр.= -1,65. u_расч. > u_кр., поэтому следует принять нулевую гипотезу Н₀, то есть выборочная и гипотетическая генеральная средняя статистически различаются не значимо.

в) По условию конкурирующая гипотеза имеет вид 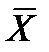>38,1, поэтому критическая область правосторонняя. Найдем критическую точку из равенства Ф(u_кр.,a)=(1-2a)/2=(1-0,1)/2=0,45. Согласно приложения 1: u_кр.=+1,65. u_расч. > u_кр.. поэтому следует отклонить нулевую гипотезу Н₀, то есть выборочная и гипотетическая генеральная средняя статистически различаются значимо.

Пример. Оценить существенность различий в средней урожайности двух сортов озимой пшеницы, если для первого сорта средняя урожайность 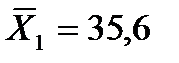ц/га и выборочная дисперсия 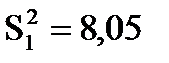, а для второго сорта средняя урожайность 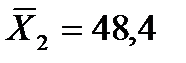и выборочная дисперсия 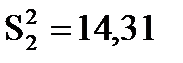. Объемы выборок n₁=5 и n₂=5 соответственно.

Решение. Выдвигаем нулевую гипотезу о том, что средние урожайности двух сортов пшеницы не отличаются друг от друга, т.е. 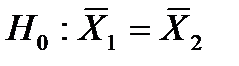, при альтернативной гипотезе 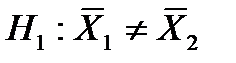-урожайности существенно различны.

Примем уровень значимости 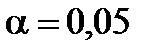.Так как выборки независимы, причем 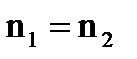,то применим критерий t – Стьюдента с 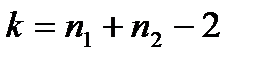степенями свободы.

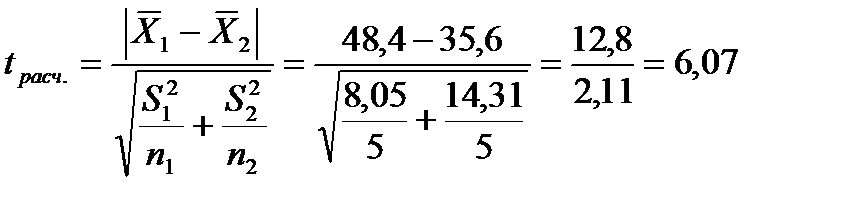. (11.8)

Критическое значение t-распределения: 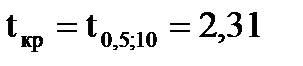,при числе степеней свободы .

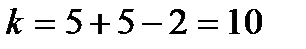Так как t_расч. > t_кр , то нулевую гипотезу следует отклонить. Следовательно, два сорта пшеницы отличаются статистически значимо по величине урожайности.

Если проверяется нулевая гипотеза о равенстве двух выборочных средних ( 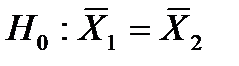), при конкурирующей гипотезе 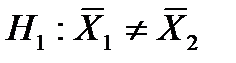( уровень значимости принять равным 0,05), то используется критерий t – Стьюдента с 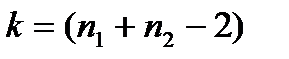степенями свободы:

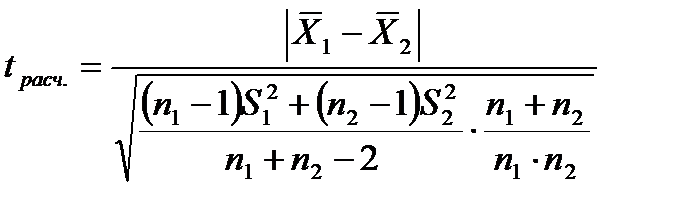. (11.9)

Пример. Два сорта озимой пшеницы испытывались на одинаковом числе участков на протяжении семи лет (табл.8).

При уровне значимости 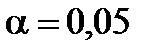проверить нулевую гипотезу о существенности различий в урожайности двух сортов озимой пшеницы.

Решение. Так как имеются две зависимости выборки, т.е. существует определенная корреляция между урожайностью сортов по годам, то необходимо оценить значимость не разности двух выборочных средних, а средней разности.

Выдвигаем нулевую гипотезу: средняя величина различий в урожайности пшеницы равна нулю, 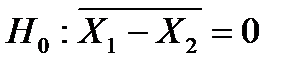при .

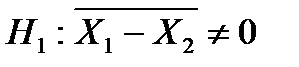Вспомогательная таблица для расчета ошибки средней разности

Год	Урожайность, ц/га	Разность
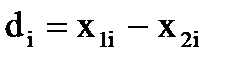
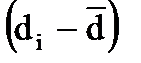
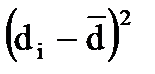
х2i	x1i
			-1	-6
Сумма

. По данным таблицы найдем среднюю разность 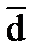и ошибку средней разности :

; ; ,

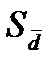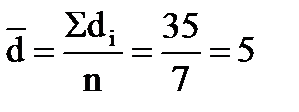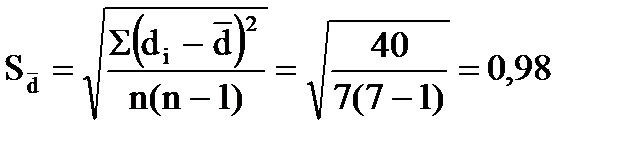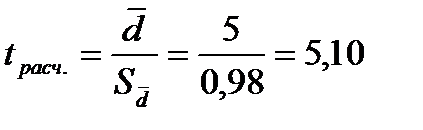где 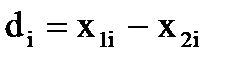, n – число пар наблюдений.

При 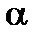=0,05; k=n-1=7-1=6, t_кр.=2,45

Сопоставив расчётное значение t с критическим, можно сделать вывод, что два сорта существенно различаются по уровню урожайности.