Двухфакторный дисперсионный анализ. Факторы А и В
Основное уравнение двухфакторного дисперсионного анализа
SS = SS 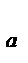 + SS
+ SS 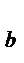 + SS
+ SS 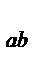 + SS
+ SS 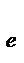 (12.17)
(12.17)
Одинаковое число повторных опытов (m = 1,2,…,n):
SS = 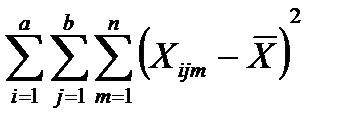 , (12.18)
, (12.18)
где SS - общая сумма квадратов разностей наблюдений и их среднего значения (сумма квадратов общих эффектов);
SS 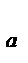 = bn
= bn 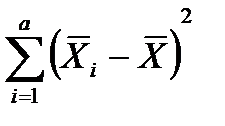 , (12.19)
, (12.19)
где SS - вклад в общую сумму квадратов, обусловленный различиями в уровнях фактора А, или взвешенная сумма квадратов эффектов фактора А (сумма квадратов между группами);
SS 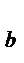 = an
= an 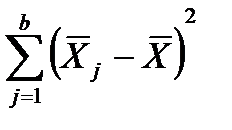 , (12.20)
, (12.20)
где SS 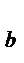 - взвешенная сумма квадратов эффектов фактора B (сумма квадратов между группами);
- взвешенная сумма квадратов эффектов фактора B (сумма квадратов между группами);
SS 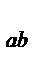 = n
= n 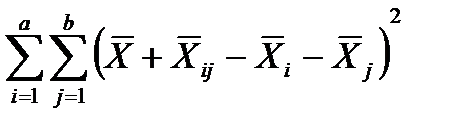 , (12.21)
, (12.21)
где SS 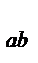 - взвешенная сумма квадратов взаимодействия уровней факторов А и В или смешанный эффект факторов А и В (сумма квадратов между группами);
- взвешенная сумма квадратов взаимодействия уровней факторов А и В или смешанный эффект факторов А и В (сумма квадратов между группами);
SS 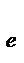 =
= 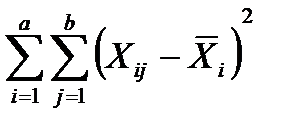 , (12.22)
, (12.22)
где SS 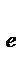 - сумма квадратов внутри групп – остаток, вклад в общую сумму квадратов, вызванный случайной изменчивостью данных внутри групп;
- сумма квадратов внутри групп – остаток, вклад в общую сумму квадратов, вызванный случайной изменчивостью данных внутри групп;
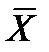 =
= 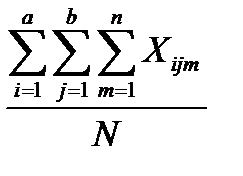 , (12.23)
, (12.23)
где 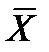 - общее среднее, N = abn – общее число опытов;
- общее среднее, N = abn – общее число опытов;
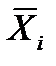 =
= 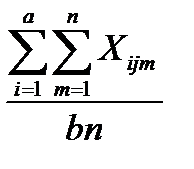 ,
, 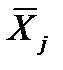 =
= 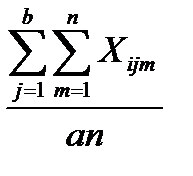 , (12.24)
, (12.24)
где 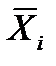 ,
, 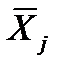 - средние значения на i уровне фактора А, j уровне фактора B соответственно.
- средние значения на i уровне фактора А, j уровне фактора B соответственно.
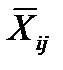 =
= 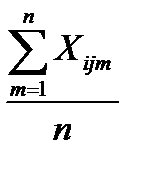 , (12.25)
, (12.25)
где 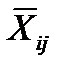 - среднее значение при различных сочетаниях уровней ij.
- среднее значение при различных сочетаниях уровней ij.
При разном числе повторных опытов (m =1,2,…,n 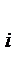 ) суммирование ведется не до n, а до n
) суммирование ведется не до n, а до n 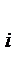 , т.е. -
, т.е. - 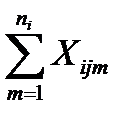 .
.
Оценки дисперсий и определение числа степеней свободы
S 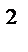 =
= 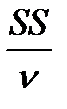 , (12.26)
, (12.26)
где 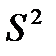 - оценка общей дисперсии;
- оценка общей дисперсии;  ν = N - 1 - число степеней свободы при определении общей дисперсии;
ν = N - 1 - число степеней свободы при определении общей дисперсии;
S 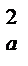 =
= 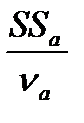 , S
, S 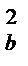 =
= 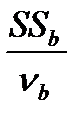 ,
,
где 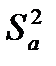 - оценка дисперсии по уровням фактора А; ν
- оценка дисперсии по уровням фактора А; ν 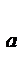 = a –1 - число степеней свободы фактора A;
= a –1 - число степеней свободы фактора A; 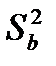 - оценка дисперсии по уровням фактора B ;
- оценка дисперсии по уровням фактора B ;
ν 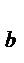 = b –1 - число степеней свободы фактора B;
= b –1 - число степеней свободы фактора B;
S 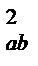 =
= 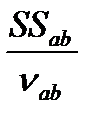 , (12.27)
, (12.27)
где 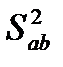 - оценка дисперсии по уровням факторов A и B;
- оценка дисперсии по уровням факторов A и B;
νab = (a –1)(b –1) -число степеней свободы взаимодействия факторов A и B;
S 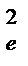 =
= 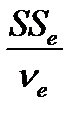 , (12.28)
, (12.28)
где 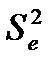 - остаточная оценка дисперсии (дисперсия ошибки);
- остаточная оценка дисперсии (дисперсия ошибки);
ν 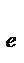 = N – ab = ab(n - 1) - число степеней свободы при определении ошибки.
= N – ab = ab(n - 1) - число степеней свободы при определении ошибки.
Общее число степеней свободы:
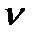 = ν
= ν 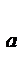 +
+ 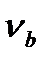 +
+ 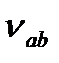 + ν
+ ν 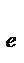 = N – 1 = (a –1)(N – a) (12.29)
= N – 1 = (a –1)(N – a) (12.29)
Проверка H 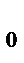 - гипотезы
- гипотезы
Определение расчетного значения критерия:
F = 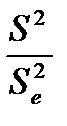 ; F
; F 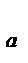
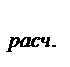 =
= 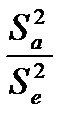 ; F
; F 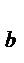
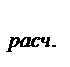 =
= 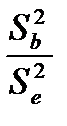 ; F
; F 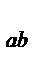
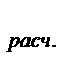 =
= 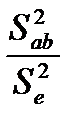 . (12.30)
. (12.30)
Критическое значение F  определяется при ν
определяется при ν 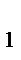 = ν
= ν 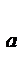 и ν
и ν 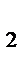 = ν
= ν 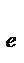 .
.
Если F 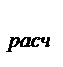
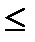 F
F  при α , ν
при α , ν 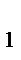 , ν
, ν 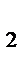 , то гипотеза H
, то гипотеза H 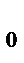 - принимается.
- принимается.
В противном случае – отклоняется и продолжается анализ гипотез о влиянии уровней факторов.
Дата добавления: 2015-08-11; просмотров: 1007;
