Оценка методом наименьших квадратов коэффициентов регрессии

В экономике большую роль играет исследование зависимостей и взаимосвязей между объективно существующими явлениями и процессами. Оно дет возможность глубже понять сложный механизм причинно-следственных отношений между явлениями. Для исследования интенсивности, вида и формы причинных влияний в эконометрике применяется корреляционно - регрессионный анализ. Он находит широкое применение при прогнозировании, при решении задач народнохозяйственного и внутрихозяйственного планирования, при выявлении факторов, воздействуя на которые можно вмешиваться в экономический процесс с целью получения нужных результатов

Под причинной связью понимают такое соединение явлений и процессов реальной действительности, когда изменение одного из них - это следствие изменения другого. Часто одно и тоже явление может выступать как результат одной или нескольких причин и в то же время само служит причиной наступления других явлений и процессов.

Функциональная связь y = f(x): для каждой независимой переменной Х существует вполне определенное значение зависимой переменной Y.

Статистическая или стохастическая (вероятностная) связь отражает закономерности только в массовых явлениях.

Статистической зависимостью называют зависимость, при которой изменение одной из величин влечет изменение распределения другой.

Статистическую зависимость называют корреляционной, если при изменении значений одной величины меняется среднее значение другой.

Корреляция означает соответствие, соотношение.

При изучении конкретных зависимостей вводят понятия:

- факторные признаки (факторы) - объясняющие, независимые переменные, причины Х. Могут быть случайными и неслучайными;

- результативные признаки (показатели) – объясняемые зависимые переменные Y, случайные.

Иногда Х и Y можно менять местами.

С корреляционным анализом тесно связан регрессионный. Их объединяют методы обработки данных, отличают цели и формы установления связи. В корреляционном анализе оценивается сила стохастической связи, в регрессионном – форма.

Регрессия – это односторонняя стохастическая зависимость, когда одна из переменных служит причиной для изменения другой.

а) Относительно характера корреляции:

− положительная (равнонаправленная, прямая);

− отрицательная (обратная).

б) Относительно числа переменных:

− простая или парная;

− множественная, с ее помощью можно охватить весь причинно-следственный комплекс;

− частная корреляция, корреляция между двумя переменными при фиксированном влиянии других (вскрывается внутренняя структура соотношений, т.е. элиминируется влияние других факторов).

в) Относительно формы связи:

− линейная;

− нелинейная.

г) Относительно типа связи явлений:

− непосредственная корреляция;

− косвенная корреляция;

− ложная корреляция.

Виды регрессии.

а) Относительно числа явлений (переменных), учитываемых в регрессии:

− простая регрессия (парная) регрессия;

− множественная или частная регрессия.

б) Относительно формы зависимости:

− линейная регрессия;

− нелинейная регрессия.

в) Относительно характера регрессии (имеет смысл только для простой линейной регрессии):

− положительная регрессия;

− отрицательная регрессия.

г) Относительно типа связи явлений:

− непосредственная регрессия – причина прямо воздействует на следствие;

− косвенная регрессия, Y и Х не состоят в прямой зависимости, а детерминируются общей для них причиной, через третью переменную;

− нонсенс- регрессия (абсурдную).

Задачи корреляционного и регрессионного анализа

а) Измерение степени связности (тесноты, силы, строгости, интенсивности) двух и более явлений:

− уточняет (верифицирует) известные связи;

− обнаруживает неизвестные.

б) Отбор факторов, оказывающих наибольшее влияние на Y, на основании степени связности – эти факторы потом используют в регрессионном анализе.

в) Обнаружение неизвестных причинных связей – непосредственно не определяет их, но устанавливает степень необходимости этих связей и достоверность суждения о них, чтобы не было «ложной» корреляции.

г) Установление формы зависимости (для случая парной регрессии):

− убывающая;

− возрастающая.

д) Определение функции регрессии.

е) Оценка неизвестных значений зависимой переменной – можно воспроизвести значение Y при заданных значениях Х внутри интервала (интерполяция) и вне интервала (экстраполяция заданных изменений Х).

Корреляционная связь чаще всего характеризуется выборочным коэффициентом корреляции r, который характеризует степень линейной функциональной зависимости между Х и Y. Коэффициент корреляции имеет следующие свойства:

;

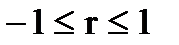Если r= ± 1, то между Х и Y существует функциональная линейная

зависимость;

Если r=0, то Х и Y некоррелированны

Если Х и Y образуют систему нормально зависимых СВ, то из их некоррелированности следует их независимость;

Коэффициенты корреляции Y на X и X наY совпадают.

Существует достаточно много методов оценки r, основные из них:

а) в случае парной зависимости - коэффициент корреляции Пирсона:

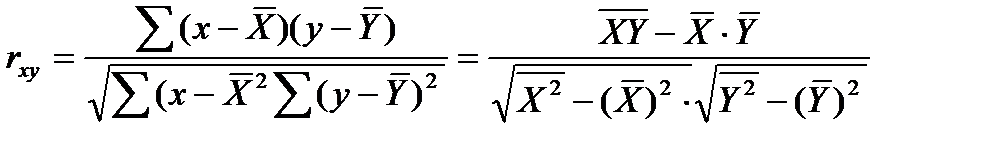, (13.1)

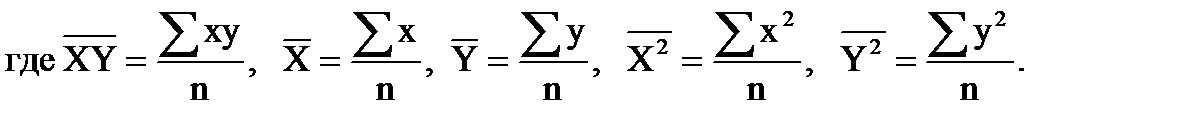
R² - множественный коэффициент детерминации, характеризующий долю зависимости независимой переменной от зависимых. Коэффициент корреляции характеризует степень линейной зависимости между переменными. Нелинейная связь не обнаруживается. В этом случае для оценки используется корреляционное отношение. Корреляционным отношением Y и X называется отношение межгруппового среднего квадратического отклонения δ_y переменной Y к её общему среднему квадратическому отклонению σ_y

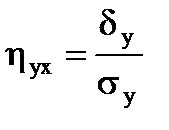, (13.2)

где межгрупповая дисперсия определяется по формуле

.

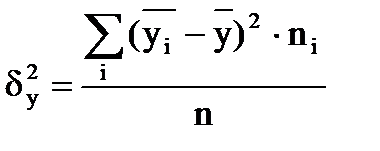.Основные свойства корреляционных отношений:

1) ;

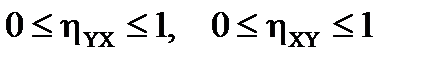2) если η=0,то корреляционная связь отсутствует;

3) если η=1,то переменные связаны функционально;

4) для линейной зависимости между переменными X иY необходимо и достаточно, чтобы выполнялось равенство ;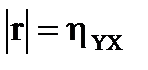

5) η_XY 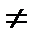η_YX;

6)

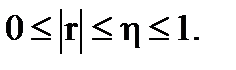
В других случаях (когда вид распределения неизвестен) используют меры связи, не регламентирующие нормальность выборок (методы непараметрической статистики), например, коэффициент ранговой корреляции Спирмена -r_s:

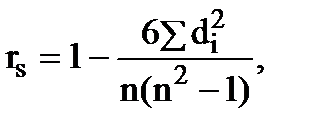(13.3)

где 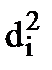- квадраты разности рангов,

n - число наблюдений (число пар рангов).

Ранг - это порядковый номер значений признака, расположенных в порядке возрастания или убывания их величин.