Оценка методом наименьших квадратов коэффициентов регрессии. По результатам эксперимента могут быть определены не «истинные» коэффициенты регрессии b, соответствующие генеральной совокупности

По результатам эксперимента могут быть определены не «истинные» коэффициенты регрессии b, соответствующие генеральной совокупности, а лишь их оценки B = (b₀,b₁, … ,b_j,…, b_d), вычисленные по выборке объемом n. В этом случае уравнение регрессии в векторной форме имеет вид:

Ŷ=h(Х,В), (13.4)

где Ŷ – предсказанные (прогнозируемые) значения выходной величины.

При выводе и использовании формул регрессионного анализа удобнее пользоваться векторной формой представления уравнений регрессии:

U=Хb+e ; Ŷ=ХВ , (13.5)

где U - вектор наблюдений; Х – матрица значений независимых переменных; b,В – векторы коэффициентов и их оценок соответственно; e - вектор ошибок:

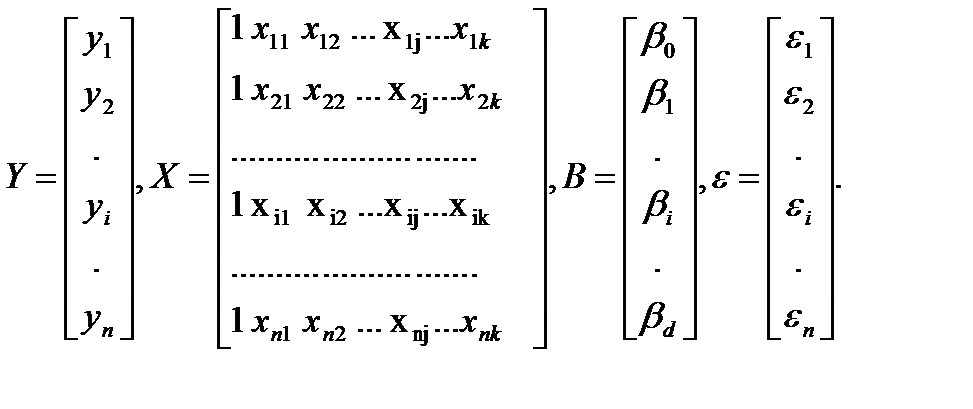
Первый столбец матрицы Х содержит фиктивную переменную

х _i0=1, i=1,2,…, n.

После вычисления коэффициентов регрессии нужно вернуться к первоначальным обозначениям для того, чтобы облегчить интерпретацию результатов.

Задачи регрессионного анализа:

вычисление коэффициентов регрессии;

проверка значимости коэффициентов регрессии;

проверка адекватности модели;

выбор “лучшей” регрессии;

- вычисление стандартных ошибок.

Проверка адекватности модели основана на методах дисперсионного анализа.

Парная регрессия.Рассмотрим решение системы нормальных уравнений в простейшем случае – линейная регрессия от одного фактора х, число определяемых коэффициентов: d=2; 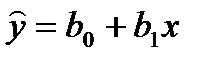Система нормальных уравнений

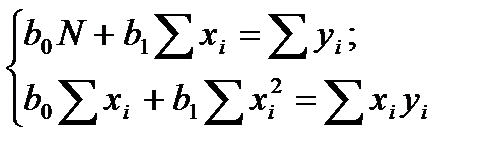
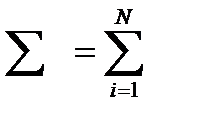(13.6)

Ршив систему (4.4.8′′) относительно b₀ и b₁, получим искомое уравнение, которое носит название регрессии Y на Х.

Если Х и Y - система двух нормально распределенных случайных величин, то, преобразуя (13.6) уравнение регрессии Y на Х можно записать:

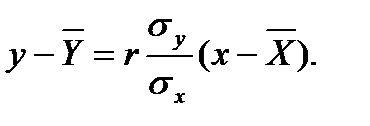(13.7)

Соответственно уравнение регрессии Х на Y:

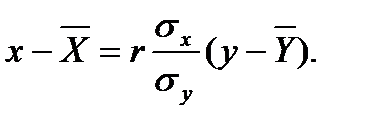(13.8)

После построения уравнения регрессии возникает вопрос о качестве решения. Адекватность линии регрессии зависит от того, какая часть суммы квадратов относительно среднего обусловлена суммой квадратов относительно регрессии, а какая суммой квадратов обусловленной регрессией. Суммы квадратов связаны с некоторым числом - числом их степеней свободы n=df. Это число показывает, сколько независимых элементов информации (из n чисел y_1, y_2,...,y_n) необходимо для образования данной суммы квадратов.

Для построения таблицы дисперсионного анализа необходимо получить средние квадраты (MS), для этого каждая сумма SS делится на соответствующие число степеней свободы df ( ).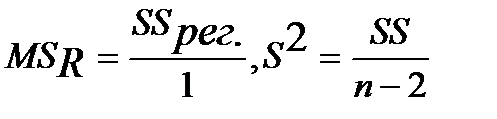

Если в уравнении регрессии (y=b₀+b₁x) b₁=0, то величина 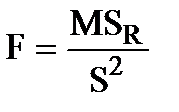распределена по распределению Фишера c (1, n-2) степенями свободы. Этот факт используется для проверки гипотезы Н₀: b₁=0 с уровнем значимости a (риском ошибиться не более чем в a100% случаев), против альтернативы Н₁: b₁¹0.

Обобщим все в таблице дисперсионного анализа

Таблица дисперсионного анализа (основное разложение)

Источник вариации	Число степеней свободы, df	Суммы квадратов, SS	Средние квадраты, MS	Fрасч.	Fкр.
Обусловленный регрессией		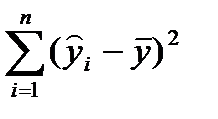	MSR		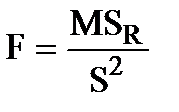Fa(1, n-2)
Относительно регрессии (остаток)	n-2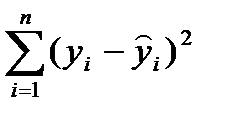
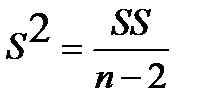
Общий, скорректирован-ный на среднее Y	n-1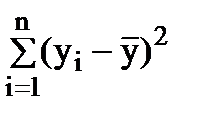

Если F_расч.>F_кр. при заданном уровне значимости a и соответствующих числах степеней свободы, то гипотеза Н₀: b₁=0 отбрасывается с риском ошибиться не более чем в a100% случаев (и уравнение регрессии считается статистически значимым).

Доля суммы квадратов, объясняемая регрессией называется множественным коэффициентом детерминации (квадратом множественного коэффициента корреляции R):

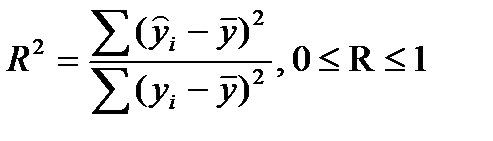. (13.9)

Значимость R² определяется по F-критерию. 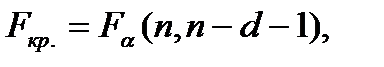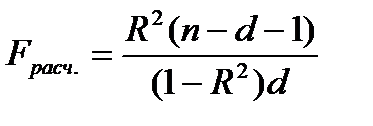. Если F_расч.>F_кр., то гипотезу Н₀:R=0 отвергают и связь между x и y считают статистически значимой. Если Y зависит только от одной переменной Х, то R=r - парному коэффициенту корреляции.