Понятие и модели дисперсионного анализа.
Дисперсионный анализ, как метод исследования, появился в работах Р. Фишера (1918-1935 гг.) в связи с исследованиями в сельском хозяйстве для выявления условий, при которых испытываемый сорт с/х культуры даёт максимальный урожай. дальнейшее развитие дисперсионный анализ получил в работах Йеитса. Дисперсионный анализ позволяет ответить на вопрос о наличии существенного влияния некоторых факторов на изменчивость фактора, значения которого могут быть получены в результате опыта. При проверке статистических гипотез предполагается случайность вариации изучаемых факторов. В дисперсионном анализе один или несколько факторов изменяются заданным образом, причём, эти изменения могут влиять на результаты наблюдений. Исследование такого влияния и является целью дисперсионного анализа.
В настоящее время наблюдается все более широкое использование дисперсионного анализа в экономике, социологии, биологии и др., особенно, после появления программных средств, снявших проблемы громоздкости статистических вычислений.
В практической деятельности, в различных областях науки мы часто сталкиваемся с необходимостью оценить влияние различных факторов на те или иные показатели. Часто эти факторы имеют качественный характер (например, качественным фактором, влияющим на экономический эффект, может быть введение новой системы управления производством) и тогда дисперсионный анализ приобретает особую ценность, так как становится единственным статистическим способом исследования, дающим такую оценку.
Дисперсионный анализ дает возможность установить, существенное ли влияние оказывает тот или иной из рассматриваемых факторов на изменчивость признака, а также определить количественно «удельный вес» каждого из источников изменчивости в их общей совокупности. Но дисперсионный анализ позволяет дать положительный ответ лишь о наличии существенного влияния, в противном случае вопрос остается открытым и требует дополнительных исследований (чаще всего – увеличения числа опытов).
В дисперсионном анализе используются следующие термины.
Фактор (Х) – то, что как мы считаем, должно оказывать влияние на результат (результативный признак) Y.
Уровень фактора (или способ обработки, иногда буквально, например – способ обработки почвы) – значения (Х 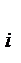 , i = 1,2,…I), которые может принимать фактор.
, i = 1,2,…I), которые может принимать фактор.
Отклик – значение измеряемого признака (величина результата Y 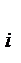 ).
).
Техника дисперсионного анализа меняется в зависимости от числа изучаемых независимых факторов. Если факторы, вызывающие изменчивость среднего значения признака, принадлежат одному источнику, то мы имеем простую группировку, или однофакторный дисперсионный анализ и далее, соответственно, двойная группировка – двухфакторный дисперсионный анализ, трехфакторный дисперсионный анализ,…, m- факторный. Факторы в многофакторном анализе принято обозначать латинскими буквами: А, В, С и т.д.
Задача дисперсионного анализа - исследование влияния тех или иных факторов (или уровней факторов) на изменчивость средних значений наблюдаемых случайных величин.
Сущность дисперсионного анализа. Дисперсионный анализ состоит в выделении и оценке отдельных факторов, вызывающих изменчивость. С этой целью производят разложение общей дисперсии 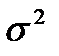 наблюдаемой частичной совокупности (общей дисперсии признака), вызванной всеми источниками изменчивости, на составляющие дисперсии, порожденные независимыми факторами. Каждая из этих составляющих дает оценку дисперсии
наблюдаемой частичной совокупности (общей дисперсии признака), вызванной всеми источниками изменчивости, на составляющие дисперсии, порожденные независимыми факторами. Каждая из этих составляющих дает оценку дисперсии 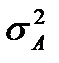 ,
, 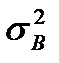 ,…, вызванную конкретным источником изменчивости, в общей совокупности. Для проверки значимости этих составляющих оценок дисперсии их сравнивают с общей дисперсией в общей совокупности (по критерию Фишера).
,…, вызванную конкретным источником изменчивости, в общей совокупности. Для проверки значимости этих составляющих оценок дисперсии их сравнивают с общей дисперсией в общей совокупности (по критерию Фишера).
Например, в двухфакторном анализе мы получим разложение вида:

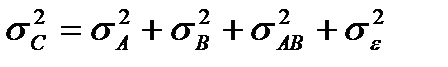 , (12.1)
, (12.1)
где
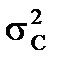 - общая дисперсия изучаемого признака C;
- общая дисперсия изучаемого признака C;
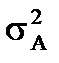 - доля дисперсии, вызванная влиянием фактора А;
- доля дисперсии, вызванная влиянием фактора А;
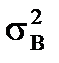 - доля дисперсии, вызванная влиянием фактора В;
- доля дисперсии, вызванная влиянием фактора В;
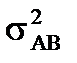 - доля дисперсии, вызванная взаимодействием факторов А и В;
- доля дисперсии, вызванная взаимодействием факторов А и В;
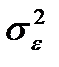 - доля дисперсии, вызванная неучтёнными случайными причинами (случайная дисперсия);
- доля дисперсии, вызванная неучтёнными случайными причинами (случайная дисперсия);
В дисперсионном анализе рассматривается гипотеза: Н0 – ни один из рассматриваемых факторов не оказывает влияния на изменчивость признака. Значимость каждой из оценок дисперсии проверяется по величине её отношения к оценке случайной дисперсии и сравнивается с соответствующим критическим значением, при уровне значимости a, с помощью таблиц критических значений F-распределения Фишера-Снедекора (прил.4). Гипотеза Н0 относительно того или иного источника изменчивости отвергается, если Fрасч.>Fкр. (например, для фактора В: SB2/Sε2 >Fкр. ).
В дисперсионном анализе рассматриваются эксперименты 3-х видов:
а) эксперименты, в которых все факторы имеют систематические (фиксированные) уровни;
б) эксперименты, в которых все факторы имеют случайные уровни;
в) эксперименты, в которых есть факторы, имеющие случайные уровни, а так же факторы, имеющие фиксированные уровни.
Случаи а), б), в) соответствуют трем моделям, которые рассматриваются в дисперсионном анализе.
Исходные данные для дисперсионного анализа обычно представляются в виде следующей табдицы:
| Номер наблюдения j | Уровни фактора | |||
| А1 | А2 | … | Ар | |
| X11 | X21 | … | Xp1 | |
| X12 | X22 | … | Xp2 | |
| X13 | X23 | … | Xp3 | |
| . | . | . | … | … |
| . | . | . | … | … |
| . | . | . | … | … |
| n | X1n | X2n | … | Xpn |
| ИТОГИ |
Рассмотрим единичный фактор, который принимает р различных уровней, и предположим, что на каждом уровне сделано n наблюдений, что дает N=np наблюдений. (Ограничимся рассмотрением первой модели дисперсионного анализа – все факторы имеют фиксированные уровни.)
Пусть результаты представлены в виде Xij (i=1,2…,р; j=1,2,…,n).
Предполагается, что для каждого уровня n наблюдений имеется средняя, которая равна сумме общей средней и ее вариации обусловленной выбранным уровнем:
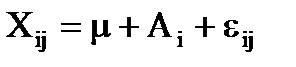 , (12.2)
, (12.2)
где m - общая средняя;
Ai - эффект, обусловленный i – м уровнем фактора;
eij – вариация результатов внутри отдельного уровня фактора. С помощью члена eij принимаются в расчет все неконтролируемые факторы .
Пусть наблюдения на фиксированном уровне фактора нормально распределены относительно среднего значения m + Ai с общей дисперсией s2.
Тогда (точка вместо индекса обозначает усреднения соответствующих наблюдений по этому индексу):
А.Xij – X.. = (Xi. – X..) + (Xij – Xi.). (12.3)
После возведения обеих частей уравнения в квадрат и суммирования по i и j получим:

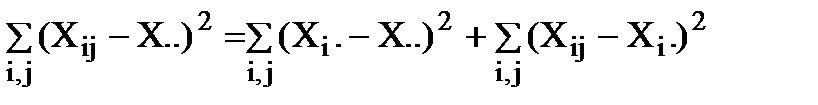 ,
,
так как 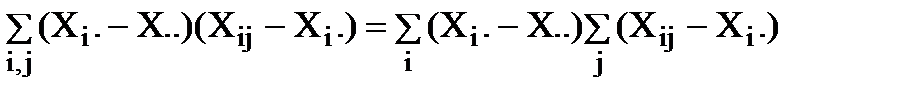 , но
, но 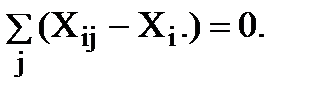
Иначе сумму квадратов можно записать: S = S1 + S2 . Величина S1 вычисляется по отклонениям p средних от общей средней X.., поэтому S1 имеет (p-1) степеней свободы. Величина S2 вычисляется по отклонениям N наблюдений от р выборочных средних и, следовательно, имеет N-р = np - p=p(n-1) степеней свободы. S имеет (N-1) степеней свободы. По результатам вычислений строится таблица дисперсионного анализа .
Таблица дисперсионного анализа
| Источник изменчивости | Суммы квадратов (SS) | Степени свободы (df) | Средние квадраты (MS) |
| Различия между уровнями | 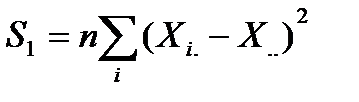
| p-1 | 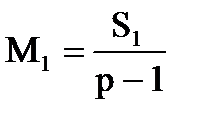
|
| Различия внутри уровней | 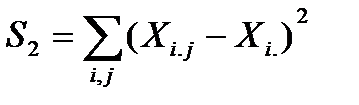
| N-p | 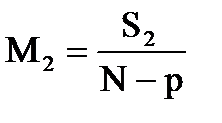
|
| Сумма | 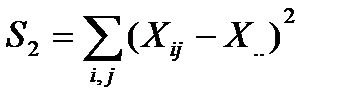
| N-1 |
Если гипотеза о том, что влияние всех уровней одинаково, справедлива, то обе величины М1 и М2 (средние квадраты) будут несмещенными оценками s2. Значит, гипотезу можно проверить, вычислив отношение (М1/М2) и сравнив его с Fкр. с ν1= (р-1) и ν2 = (N-p) степенями свободы .
Если Fрасч.>Fкр., то гипотеза о незначимом влиянии фактора А на результат наблюдений не принимается.
Для оценки существенности различий при Fрасч.  Fтабл. вычисляют:
Fтабл. вычисляют:
а) ошибку опыта
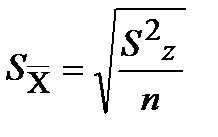 (12.4)
(12.4)
б) ошибку разности средних
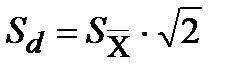 (12.5)
(12.5)
в) наименьшую существенную разность
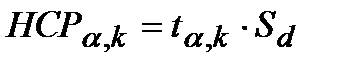 (12.6)
(12.6)
Сравнивая разность средних значений 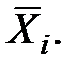 по вариантам с НСР, делают вывод о существенности различий в уровне средних.
по вариантам с НСР, делают вывод о существенности различий в уровне средних.
Замечание. Применение дисперсионного анализа предполагает, что:
1) М(εij)=0,
2) D(εij)=σ2= const,
3) εij → N (0, σ ) или xij→ N (a, σ ).
Дата добавления: 2015-08-11; просмотров: 1056;
