Уровень значимости. Мощность критерия.
1)Понятие и виды статистических гипотез.
Статистической гипотезой называется всякое высказывание о генеральной совокупности, проверяемое по выборке. Статистические гипотезы делятся на:
Параметрические - это гипотезы, сформулированные относительно параметров (среднего значения, дисперсии и т.д.) распределения известного вида;
Непараметрические - это гипотезы, сформулированные относительно вида распределения (например, определение по выборке степени нормальности генеральной совокупности).
Процесс использования выборки для проверки гипотезы называется статистическим доказательством. Основную выдвигаемую гипотезу называют нулевой H0. Наряду с нулевой гипотезой рассматривают ей альтернативную H1. Например, H0: M(х)=1, математическое ожидание генеральной совокупности равно 1; H1: M(х)>1, или M(х)<1, или M(х) 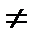 1 (математическое ожидание больше 1, или меньше 1, или не равно 1).
1 (математическое ожидание больше 1, или меньше 1, или не равно 1).
Выбор между гипотезами H0 и H1 может сопровождаться ошибками двух родов. Ошибка первого рода α означает вероятность принятия H1, если верна гипотеза H0: 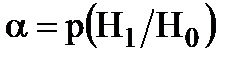 . Ошибка второго рода означает вероятность принятия H0, если верна гипотеза H1:
. Ошибка второго рода означает вероятность принятия H0, если верна гипотеза H1: 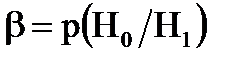 . Существует правильное решение двух видов:
. Существует правильное решение двух видов: 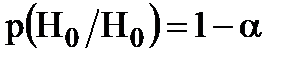 и
и 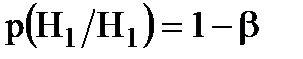 .
.
Ошибки первого и второго рода
| Принятая гипотеза | Н0 | Н1 |
| H0 - верна | P(Н0/Н0)=1-a | P(Н1/Н0)=a |
| H0 – неверна | P(Н0/Н1)=b | P(Н1/Н1)=1-b |
Правило, по которому принимается решение о том, что верна или не верна гипотеза Н0, называется критерием, где:
a=P(Н1/Н0) - уровень значимости критерия;
M=1-b=P(Н1/Н1) - мощность критерия.
Дата добавления: 2015-08-11; просмотров: 1220;
