Статистические оценки выборочной совокупности и их свойства.

Важнейшей задачей выборочного метода является оценка параметров генеральной совокупности по данным выборки.

Пусть 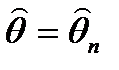- выборочная характеристика, вычисленная по результатам n наблюдений величины Х, используемая в качестве оценки q - характеристики генеральной совокупности (в качестве q может быть M(X), D(X) и т.д.).

Качество оценки 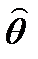устанавливается по трем свойствам: состоятельность, несмещенность, эффективность.

1. Состоятельность. Оценка 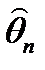является состоятельной оценкой генеральной характеристики q, если для любого ε > 0 выполняется следующее равенство

Это означает, что при увеличении объема выборки n выборочная характеристика .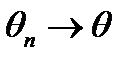

2. Несмещенность. Оценка 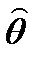генеральной характеристики q называется несмещенной, если для любого фиксированного числа наблюдений n выполняется равенство .

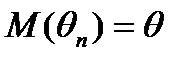3. Эффективность. Несмещенная оценка 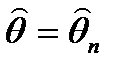генеральной характеристики 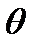называется несмещенной эффективной, если среди всех подобных оценок той же характеристики она имеет наименьшую дисперсию:

D( 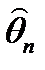) ® min.

Можно показать, что статистики 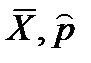являются состоятельными, несмещенными и эффективными характеристиками математического ожидания M(X) и вероятности р соответственно.

Выборочная дисперсия 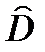(далее по тексту 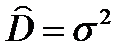) не обладает свойством несмещенности. На практике используют исправленную выборочную дисперсию S², которая является несмещенной оценкой дисперсии генеральной совокупности:

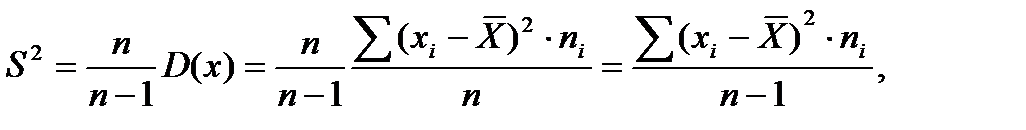(10.1)

S - стандартное отклонение.

Кроме того, в расчётах используют стандартную ошибку выборки:

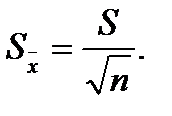(10.2)