Определение необходимой численности выборки.
Для построения доверительного интервала параметра a – математического ожидания нормального распределения составляют выборочную характеристику (статистику), функционально зависимую от наблюдений и связанную с a, например, для повторного отбора:
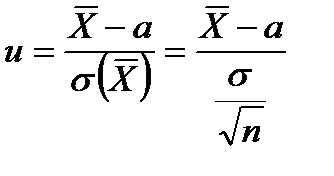 . (10.5)
. (10.5)
Статистика u распределена по нормальному закону распределения с математическим ожиданием a = 0 и средним квадратическим отклонением s=1. Отсюда,
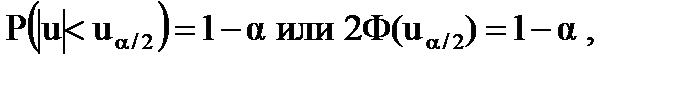
где Ф − функция Лапласа, uα/2 − квантиль нормального закона распределения, соответствующая уровню значимости a. Доверительный интервал для параметра а:
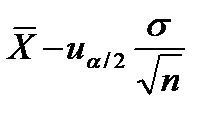 < a <
< a < 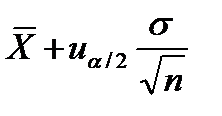 , (10.6)
, (10.6)
где 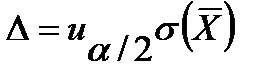 - предельная ошибка выборочной средней.
- предельная ошибка выборочной средней.
Формулы предельной ошибки и необходимого объема выборки
для различных способов отбора В таблице:
1) t – квантиль распределения, соответствующая уровню значимости a,
а) при n³30 t=ua/2 - квантиль нормального закона распределения (прил.1),
б) при n<30 t - квантиль распределения Стьюдента с ν=n-1 степенями свободы для двусторонней области (прил.3);
2) s2 – выборочная дисперсия,
а) при n³30 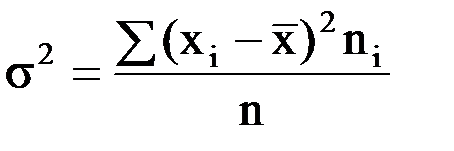 ,
,
б) при n<30 вместо s2 берут 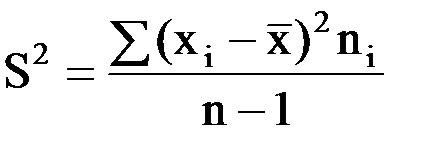 ;
;
3) pq - дисперсия относительной частоты в схеме повторных независимых испытаний;
4) N - объем генеральной совокупности;
5) n - объем выборки;
6) 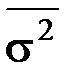 - средняя арифметическая групповых дисперсий (внутригрупповая дисперсия);
- средняя арифметическая групповых дисперсий (внутригрупповая дисперсия);
| Выборка | Собственно-случайная | Типическая | Серийная | ||||
| повторная | бесповторная | повторная | бесповторная | повторная | Бесповторная | ||
| Предельная ошибка, D | средней,
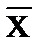
| 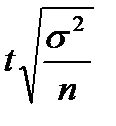
| 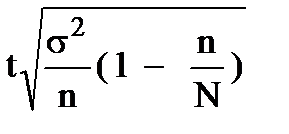
| 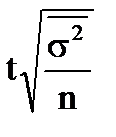
| 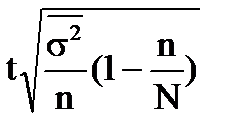
| 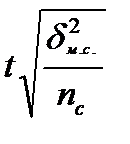
| 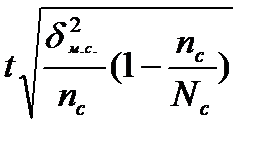
|
доли,
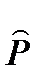
| 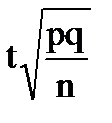
| 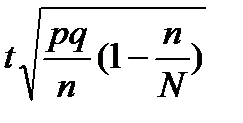
| 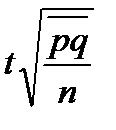
| 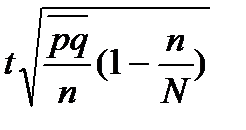
| 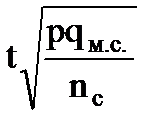
| 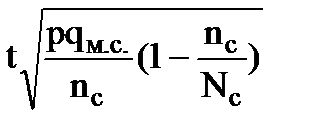
| |
| Необходимая численность, n | средней,
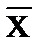
| 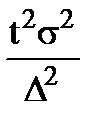
| 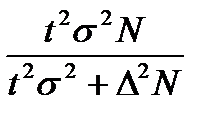
| 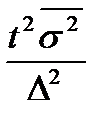
| 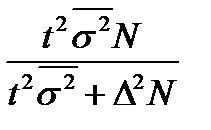
| 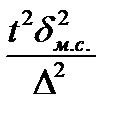
| 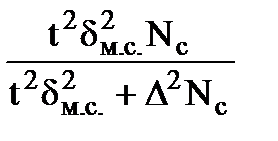
|
доли,
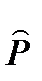
| 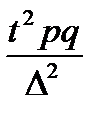
| 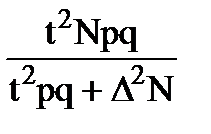
| 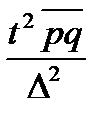
| 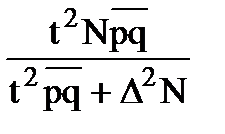
| 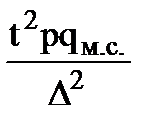
| 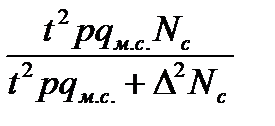
|
7) 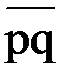 - средняя арифметическая дисперсий групповых долей;
- средняя арифметическая дисперсий групповых долей;
8) d2м.с. - межсерийная дисперсия;
9) pqм.с.- межсерийная дисперсия доли;
10) Nc - число серий в генеральной совокупности;11) nc - число отобранных серий (объем выборки);12) D - предельная ошибка выборки ( 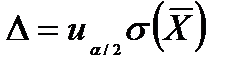 или
или 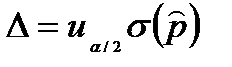 ).
).
Дата добавления: 2015-08-11; просмотров: 699;
