Распределение молекул по скоростям и энергиям. Барометрическая формула

Молекулы газа движутся с различными по величине и на­правлению скоростями. Возникает вопрос: как распределены молекулы по скоростям? Ответ на этот вопрос дал выдающий­ся английский физик Джеймс Клерк Максвелл в 1859 году. В дальнейшем это распределение стали называть "распределени­ем Максвелла".

Для краткости рассмотрим молекулы одного сорта, каждая из которых обладает массой т. Будем полагать, что все на­правления движения молекул в пространстве равновероятны. Очевидно, что молекул, обладающих нулевой скоростью, прак­тически нет; также нет и молекул, обладающих бесконечно большой скоростью (с учетом эффектов теории относительно­сти скорости молекул не могут быть равны или превышать с = 3 • 10⁸м/с). Чтобы ответить на поставленный выше вопрос, нам нужно знать, какое количество молекул попадает в задан­ный интервал скоростей. Попробуем разобраться в этом вопро­се.

Пусть общее количество молекул, содержащихся в сосуде — N. Тогда обозначим через dN количество молекул, скорости ко­торых заключены в интервале от v до v + dv. Отношение dN/dv называется плотностью распределения молекул по скоростям. Функция f(v) — dN/(Ndv) называется функцией распределения молекул по скоростям или функцией распределения Максвел­ла. При этом также полагают, что газ находится в равновесном состоянии, т.е. температура и давление газа во всех частях со­суда одинаковы. Функция f(v) дает нам плотность вероятности того, что данная молекула обладает скоростью v. Очевидно, что

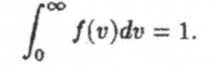
Это означает, что какой-то скоростью в интервале [0, ∞] моле­кула обязательно обладает. Вообще же, вероятность того, что скорость молекулы лежит в интервале [v,v + dv], задается соот­ношением dp = f(v)dv. Как показал Максвелл, функция распре­деления имеет вид

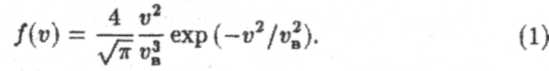
Здесь v_в = 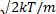_, к= 1,38 • 10^-23Дж/К — постоянная Больцмана, Т — абсолютная температура газа. График функции распределения показан на рисунке 1.

Максимуму кривой распределения соответствует скорость v_в, называемая наиболее вероятной скоростью. Ее значение легко определяется, если производную от функции (1) прирав­нять к нулю. Тогда можно убедиться, что эта производная 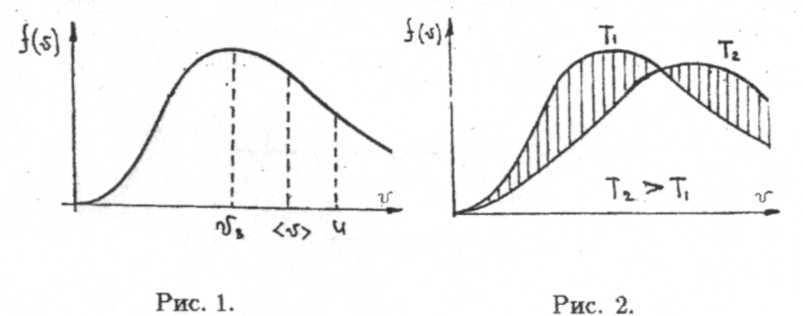обращается в нуль при v = t>„; причем, экстремум, имеющий место в этой точке, соответствует максимуму функции распределения. Две другие характерные скорости (v) — средняя ариф­метическая и u — средняя квадратичная находятся из соотношений

Здесь μ — молярная масса газа, т — масса молекулы газа, R — универсальная газовая постоянная. Заметим, что с ростом тем­пературы T максимум функции распределения смещается впра­во вдоль оси v. При этом площадь под кривой распределения в силу определения функции f(v) не изменяется.

На рисунке 2 качественно показаны две кривые распределе­ния при различных температурах. Заштрихованные площади на рисунке 2 должны быть одинаковы.