Связь между давлением и температурой газа

Объединяя уравнение Клаузиуса (5) и Больцмана (6), получим:

Из уравнения (7) определим постоянную Лошмидта (N_l),т.е. число молекул в единице объема газа при нормальных услови­ях:

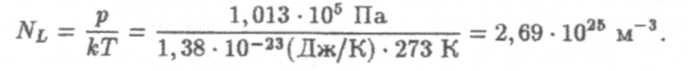
По постоянной Лопшидта можно получить число Авогадро:

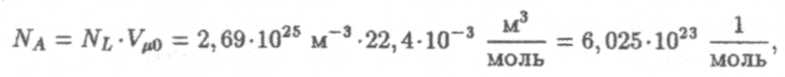
где V_μ0 — объем моля газа при нормальных условиях.

Уравнения (5), (7) являются основными уравнениями молекулярно-кинетической теории газа. Из них можно теоретически вывести (как следствия) все экспериментальные газовые законы (к чему мы и переходим).

Вывод экспериментальных газовых законов из молекулярно-кинетической теории газа

а) Вывод уравнения Клапейрона-Менделеева (уравнения со­стояния идеального газа).

В уравнение (7) введем п = N/V, учитывая, что N/N_A = т/μ, где N — число молекул в объеме газа, т и μ — масса и молярная масса газа. Тогда получим:

— уравнение Клапейрона-Менделеева для любой массы газа, где R = kN_a молярная газовая постоянная. Для одного моля газа уравнение (8) имеет вид:

где V_μ — объем моля газа. Из уравнения (9) вычислим R, зная что при нормальных условиях (T = 273 К, р = 1,013 • 10⁵ Па) молярный объем равен 22,4 • 10^-3 м³/моль; для газовой по­стоянной R имеем:

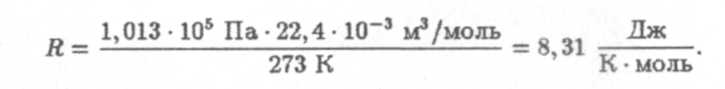
Тогда определится и постоянная Больцмана;

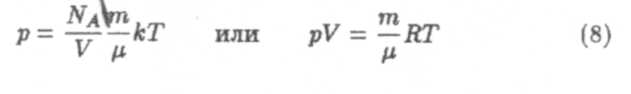
б) Вывод закона Клапейрона. Из уравнения (9) запишем:

Обозначим (m/μ)R — В, тогда:

— закон Клапейрона. В отличие от R, В не универсальна, а своя для каждого газа из-за различия молярной массы.

в) Вывод закона Бойля-Мариотта (для изотермического

процесса). Согласно формуле (9) и учитывая, что для данной массы газа: т = const; μ = const; Т = const, имеем:

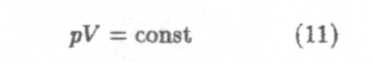
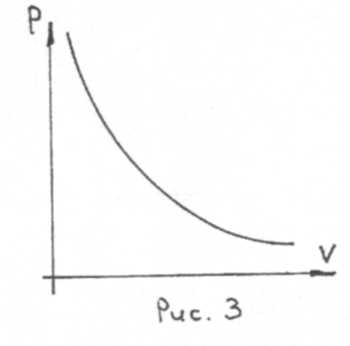
— закон Войля-Мариотта.

Для данной массы газа произведе­ние давления на объем при посто­янной температуре остается по­стоянным.

Очевидно, что график изотермического процесса предста­вляется равнобочной гиперболой (рис. 3).

г) Вывод закона Гей-Люссака (для изобарического процес­са). Напишем уравнение (8) для двух состояний газа при посто­янном давлении — для любого и нормального состояний:

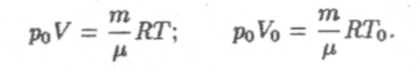
Поделив первое уравнение на второе, получим:

—закон Гей-Люссака.

При изобарическом процессе объем газа пропорционален его термодинамической температуре.

Этот закон можно представить и в другой форме:

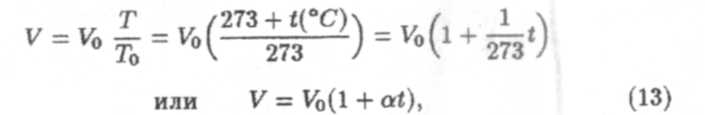
где а = 1/273 К^-1 — коэффициент объемного расширения газа.

Для данной массы газа объем газа при постоянном давлении изменяется линейно с температурой.

Графиком закона является наклонная линия, исходящая из ОК (-273^вС) (рис.4).

д) Вывод закона Шарля (для изохорического процесса). На­пишем уравнение (9) при V = const и т = const для любого и нормального состояний

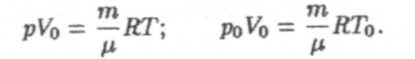
Поделив первое уравнение на второе, получим:

—закон Шарля.

При изохорическом процессе давление газа пропорционально его термодинамической температуре.

Закону можно также придать вид:

где τ — термический коэффициент давления (7 = 1/273 К^-1).

Для данной массы газа при постоянном давлении объем газа изменяется линейно с температурой.

График данного закона изображен на рис. 5.

е) Вывод закона Дальтона. Пусть в некотором объеме содер­жится несколько различных газов. Давление смеси — р. Уда­лим из объема все газы, кроме первого. Тогда он займет весь объем и будет иметь давление p₁, называемое парциальным да­влением первого газа (part — часть).

Парциальным давлением газа, входящего в газовую смесь, называется давление, которое имел бы этот газ, если бы он один занимал весь объем, предоставленный смеси.

Аналогично определим парциальное давление всех осталь­ных газов смеси: р₁, р₂, р₃,...р_i<. Обозначив п и п_i соответ­ственно объемные концентрации молекул смеси газов и i-го га­за, запишем:

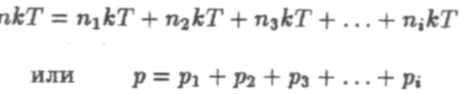
— закон Дальтона.

Давление газовой смеси равно сумме парциальных давлений входящих в нее газов.

Закон был установлен экспериментально в 1801 году англий­ским физико-химиком Дальтоном.

Вывод закона Авогадро. Из уравнения (3) молекулярно-кинетической теории получим pV = NkT. Но для одного моля газа V = Vμ и N = Na (Na — постоянная Авогадро) запишем:

Так как N_a и к —постоянные величины, то из последнего равен­ства следует закон Авогадро установленный им в 1811 году:

При одинаковой температуре и давлении моли любых газов занимают одинаковые объемы.

При нормальных условиях, т.е. при р = 1,013 • 10⁵ Па и Т = 273,16 К, этот объем составляет 0,0224 м³/моль.

Лекция № 11