Распределение Больцмана. Барометрическая формула
Рассмотрим газ, находящийся в поле тяжести Земли (в принципе, это поле можно заменить любым другим силовым полем). Будем считать температуру газа во все точках среды одинаковой и равной T. Выделим цилиндрический объем газа, показанный на рисунке 3.
Ось h направим вертикально вверх от поверхности Земли. Площадь основания цилиндра обозначим через S. Пусть p+dp — это 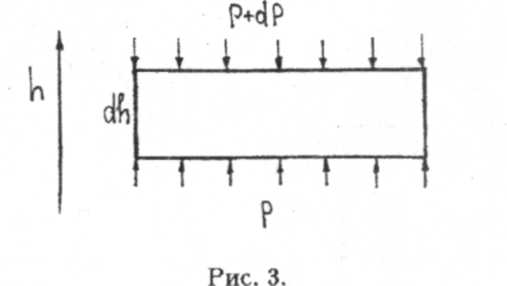
 давление на верхнее основание цилиндра, р — давление на нижнее основание цилиндра, dh — высота цилиндра. Концентрацию молекул внутри цилиндра обозначим через п. Будем полагать, что рассматриваемый цилиндрический объем находится в состоянии равновесия. Следовательно, сумма действующих на него сил должна быть равна нулю.
давление на верхнее основание цилиндра, р — давление на нижнее основание цилиндра, dh — высота цилиндра. Концентрацию молекул внутри цилиндра обозначим через п. Будем полагать, что рассматриваемый цилиндрический объем находится в состоянии равновесия. Следовательно, сумма действующих на него сил должна быть равна нулю.
На верхнее основание действует сила F = (р + dp)S, на нижнее (F + dF) = pS. Разница этих сил уравновешивается силой тяжести dMg - mgSn * dh. Здесь Sdh — объем цилиндра, dM — масса газа внутри этого объема. Отсюда имеем
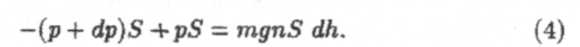
Или после небольших преобразований

|
Учитывая, что n = р/(кТ), вместо (5) получим

|
Выполним интегрирование и сделаем последующие преобразования
где ро — давление на поверхности Земли, Отсюда вместо (7) 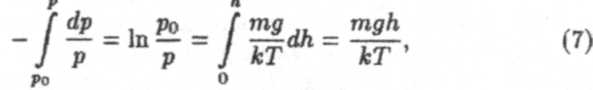
имеем

Учитывая также, что р = пкТ, получим
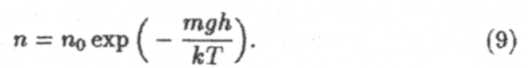
Формула (8) называется барометрической формулой. Она показывает, как меняется давление по мере увеличения высоты над поверхностью Земли. В реальной земной атмосфере давление уменьшается приблизительно в 3 раза при увеличении высоты
на 8 км. Формула (9) называется формулой Болъцмана. Она описывает распределение молекул по потенциальным энергиям.
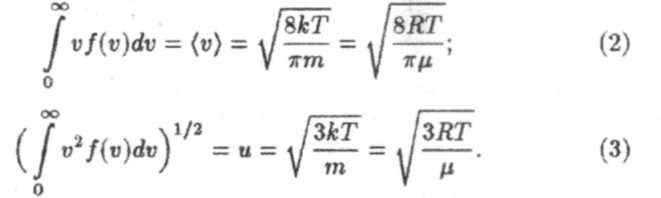
Чтобы узнать, какая часть из п молекул обладает данной скоростью, т.е. как они распределены по скоростям, п надо умножить на f(v). Тогда найдем
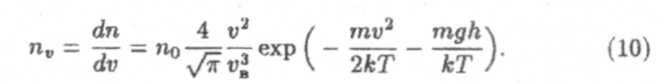
|
Формулу (10) иногда называют распределением Максвелла-Болъцмана. Ее можно привести к виду
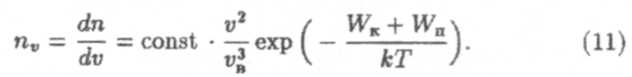
|
Здесь в числителе экспоненты стоит сумма кинетической (WK) и потенциальной (Wn) энергий молекул, т.е. ее полная механическая энергия W. Поэтому распределение (11) есть фактически распределение по энергиям и его можно записать в форме
Отметим, что формула (12) остается верной для любого силового поля, а не только гравитационного. Экспериментально закон распределения Максвелла был проверен в 1920 году немецким физиком Отто Штерном. Закон распределения Больпмана также многократно проверялся экспериментально, например, с помощью барометров, поднимаемых на различные высоты.
Дата добавления: 2015-08-11; просмотров: 891;
