Вывод основного уравнения молекулярно кинетической теории идеального газа

(уравнения Клаузиуса)

Согласно молекулярно-кинетической теории газ есть сово­купность огромного числа молекул, хаотически движущихся и сталкивающихся друг с другом и со стенками сосуда. Многочи­сленные удары о стенку сосуда создают непрерывно действую­щую на нее силу, которая, будучи поделена на площадь стенки, дает давление газа р. Эта сила, а следовательно, и давление зависит от скорости движения молекул:

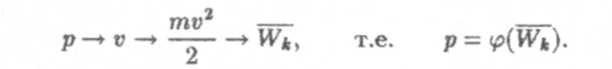
Это и есть в общем виде уравнение Клаузиуса, предложенное немецким физиком-теоретиком Рудольфом Юлиусом Эмануэ­лем Клаузиусом, профессором Цюрихского университета. Кон­кретный вид этого уравнения нам предстоит найти.

Сделаем следующие упрощающие предположения относи­тельно газа.

а) Молекулы — абсолютно упругие шарики пренебрежимо ма-
лого размера (материальные тонки). Они отскакивают от стен-
ки, изменял только направление, но не величину скорости.

б) Силы притяжения между молекулами пренебрежимо ма-
лы, а собственным объемом молекул можно пренебречь (так как
в среднем расстояние между молекулами газа гораздо больше
размеров молекул).

Газ, обладающий такими свойствами, называют идеальным газом. Очевидно, что реальный газ при условиях близких к нор­мальным, а также при высокой температуре (Т) и при низком давлении (р) весьма близок по своим свойствам к идеальному.

Выведем уравнение Клаузиуса. Пусть в сосуде с плоскими стенками находится идеальный газ, число молекул которого в единице объема обозначим через п. Массу каждой молекулы будем считаь равной т. Вследствие хаотичности движения мо­лекул газа можно полагать, что вдоль каждого из основных на­правлений в пространстве (х, у, z) движется в среднем 1/3 всех молекул, и соответственно в положительном направлении оси х — 1/6 всех молекул газа.

Рассмотрим результат удара одной такой молекулы о стен-

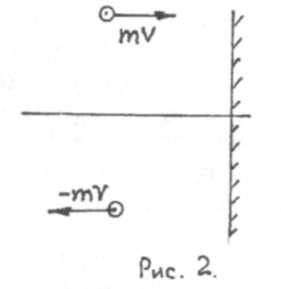
ку сосуда (рис. 2), полагая, что по­следняя расположена перпендику­лярно к оси х. До удара молеку­ла обладала импульсом mv; после удара он стал равным (—mv). В результате удара стенка получи­ла импульс ∆к = 2mv. За вре­мя t до стенки долетят молекулы, находящиеся от нее на расстоянии l= vt.

Рассмотрим участок стенки площадью ∆S; тогда за время t до нее долетят молекулы, заключенные в цилиндрическом объ­еме площадью основания ∆S с длиной образующей l, движущи­еся в положительном направлении оси х. Очевидно, что число таких молекул N будет равно:

За время t эти молекулы передадут стенке импульс

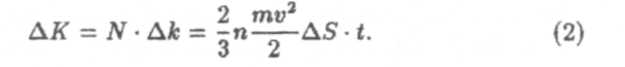
Импульс, передаваемый этими молекулами в единицу времени, численно равен силе, действующей на стенку со стороны газа придут в

Давление газа пропорционально средней кинетической анергии поступательного движения молекул газа и числу молекул в еди­нице объема.

Итак, уравнение Клаузиуса выражает макроскопическую ха­рактеристику газа р через его микроскопическую характеристи­ку W_k. Естественно предположить, что и другая макрохарак­теристика газа — его термодинамическая температура Т тоже связана с микрохарактеристикой W_k (поскольку энергия зави­сит от скорости, а скорость от температуры). Эта связь наблю­дается в уравнении Больцмана.