Стоячие волны. Если в пространстве навстречу друг другу бегут две плоских монохроматических волны равной частоты, то в пространстве
Если в пространстве навстречу друг другу бегут две плоских монохроматических волны равной частоты, то в пространстве, где эти волны накладываются друг на друга, может образоваться стоячая волна. Рассмотрим свойства и условия образования этих волн.
Стоячей волной называется волна, образующаяся в результате наложения двух бегущих гармонических волн, которые распространяются навстречу друг другу и имеют одинаковые частоты и амплитуды, а в случае поперечных волн еще и одинаковую поляризацию. При сложении двух плоских когерентных волн вида
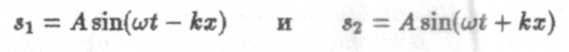
образуется стоячая волна, описываемая уравнением
Это и есть уравнение стоячей волны. Амплитуда стоячей волны Авпериодическим образом зависит от координаты x:

В стоячей волне имеются такие точки, которые остаются все время неподвижными. Они называются узлами стоячей волны.Положение этих точек определяется из условия
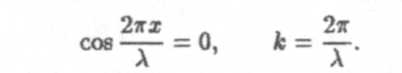
Здесь λ- длина волны. Таким образом, положение узлов на оси хопределяется с помощью формулы
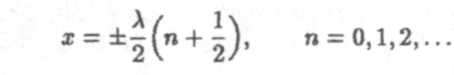
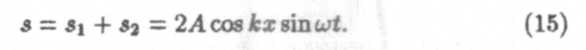

Расстояние между двумя соседними узлами равно λ/2. Точки волны, колеблющиеся с наибольшими амплитудами, называются пучностями стоячей волны. Координаты этих точек определяются из условия
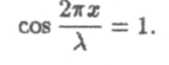
|
Это уравнение удовлетворяется при
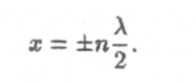
|
Расстояние между двумя соседними пучностями также равно λ/2. Перенос энергии через узлы отсутствует.
Пример. Колебания струн.
В случае свободных колебания струны, закрепленной с одного или двух концов, в ней возникают стоячие волны. Частоты этих волн могут принимать только определенные дискретные значения, называемые собственными частотамиколебаний струны. На жестко закрепленных концах струны располагаются узлы стоячей волны, а на свободном конце — пучности стоячей волны.
Если l— длина струны, а cф— фазовая скорость, то в случае струны, закрепленной на обоих концах, на длине lукладывается целое число полуволн λ/2
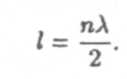
Собственные частоты колебаний такой струны будут равны
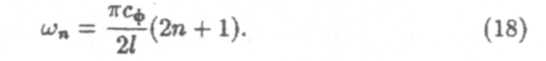
| Для струн, один конец которых закреплен, а другой свободен, имеем |
Амплитуды возбуждаемых колебаний, как правило, убывают при увеличении номера гармоники n. При n=0, в случае (17), частота ω0=πсф/l. Эту частоту называют основным тоном, а все последующие — обертонами. Частоты этих гармоник кратны ω0.
Если возбуждение колебаний производится периодической силой, изменяющейся с частотой ωп, то струна "резонирует" именно с этой частотой: колебания именно этой частоты будут иметь наибольшую амплитуду, а амплитуды других гармоник, включая основной тон, будут пренебрежимо малы.
Стоячие волны также возникают в специально сконструированных для них системах — резонаторах. Примерами подобных систем могут служить получившие в настоящее время широкое распространение лазеры.
Фазовая и групповая скорость волн
Фазовая скорость, как было отмечено нами ранее, это скорость перемещения в пространстве поверхности равной фазы. Она может принимать различные значения от 0 до со. Эта скорость определяется формулой сф = ω/k. Групповая скорость это скорость, с которой сигнал перемещается в пространстве. Она также является скоростью перемещения энергии и распространения информации в пространстве. Эта скорость не может быть больше, чем скорость света в вакууме (с = 3-108м/с). Она определяется по формуле
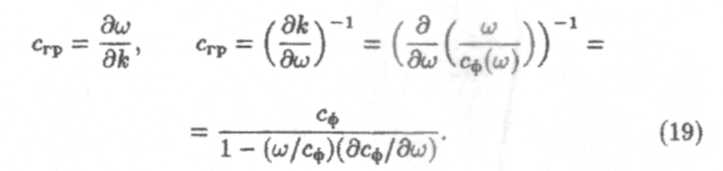
Если дисперсия отсутствует, то
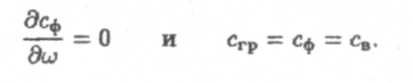
При нормальной дисперсии (см. лекцию №32) сгр < сф,а при аномальной дисперсии — наоборот. Если среда обладает сильным поглощением, то понятие групповой скорости теряет смысл.
Лекция №9
Элементы специальной теории относительности
Преобразования Галилея. Принцип относительности в механике
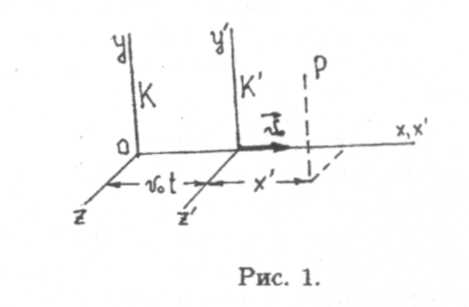
Рассмотрим две инерциальвые системы отсчета. Одну из них, обозначенную на рис. 1 буквой К, будем условно считать неподвижной. Тогда вторая система К' будет двигаться равномерно и прямолинейно. Выберем направления осей координат таким образом (как указано на рис. 1), чтобы система К' двигалась вдоль положительного направления оси х системы К со скоростью vo-
Связь между координатами произвольной точки Р в системах К и К' определяется уравнениями
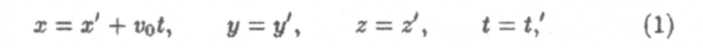
 которые носят названия преобразования Галилея. Последнее равенство t= t' соответствует принятому в классической механике предположению о том, что ход времени не зависит от выбора системы отсчета, т.е. что время абсолютно.
которые носят названия преобразования Галилея. Последнее равенство t= t' соответствует принятому в классической механике предположению о том, что ход времени не зависит от выбора системы отсчета, т.е. что время абсолютно.
Дифференцируя выражение для координат (1), можно установить закон сложения скоростей в классической механике,
который позволяет определить скорость движения v в системе К как сумму скоростей v' тела в системе К' и скорости движения vo самой системы отсчета К' относительно системы К.
Ускорения тела в системах К и К' одинаковы
Постулаты специальной теории относительности
Классическая механика Ньютона прекрасно описывает движения макротел с малыми скоростями (о <£ с). Но в конце 19 века возникли трудности при попытках объяснить движение быстрых заряженных частиц, а также при изучении скорости распространения света в различных системах отсчета. Знаменитые опыты Майкельсона-Морли (1881, 1887 гг.) показали, что скорости света в двух движущихся друг относительно друга системах отсчета равны, что противоречило классическому закону сложения скоростей (2). Л ля объяснения опытных данных необходимо было создать новую механику, включавшую ньютоновскую механику как частный случай малых скоростей (v -< с). Основы этой теории, получившей название специальной теории относительности или релятивистской теории, заложил А.Эйнштейн.
Постулаты Эйнштейна
1. Принцип относительности.
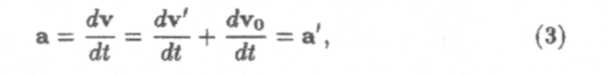
| отсюда вытекает принцип относительности Галилея: законы динамики во всех инерциальных системах отсчета одинаковы. Невозможно никакими механическими опытами установить, находится данная система отсчета в состоянии покоя или движется равномерно и прямолинейно. |
Никакие опыты (механические, электрические, оптические), проведенные внутри данной инициальной системы отсчета, не позволяют обнаружить, покоится эта система или движется равномерно и прямолинейно: все законы природы инвариантны по отношению к переходу от одной инерциальной системы к другой.
2. Принцип инвариантности скорости света.
Скорость света в вакууме не зависит от скорости дви-
жения источника света и одинакова во всех инерциальных
системах отсчета.
| Перемножал эти соотношения, получим |
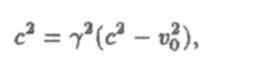
|
| откуда |
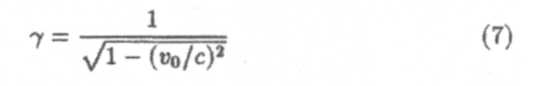
|
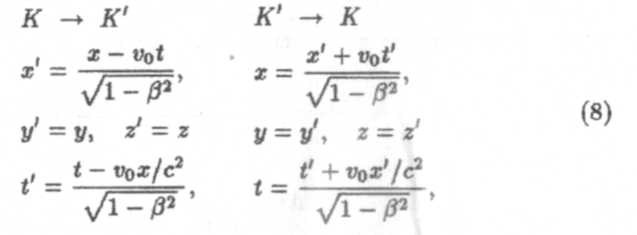
| Оперируя далее формулами (5) и (7), можно получить преобразования Лоренца для координат и времени в релятивистской механике: |

|
Первый постулат обобщает принцип относительности Галилея. Согласно второму постулату постоянство скорости света — фундаментальное свойство природы, которое констатируется как опытный факт.
Преобразования Лоренца
Преобразования Галилея (1) несовместимы с постулатами релятивистской механики. Чтобы показать это, рассмотрим системы отсчета К и К' (рис. 1) в начальный момент времени t = t' = 0, считая, что в этот момент начала координат О и О' совпадают. Предположим, что в этот момент испускается световой импульс. Скорость света в К и К' одинакова (с = const). В системе К сигнал дойдет до некоторой фиксированной точки А за время t, пройдя расстояние х = ct. В системе К' координата светового импульса в момент достижения точки А составит х' = ct'. Координаты точки А в разных системах различны, х ≠ х'. Отсюда следует, что
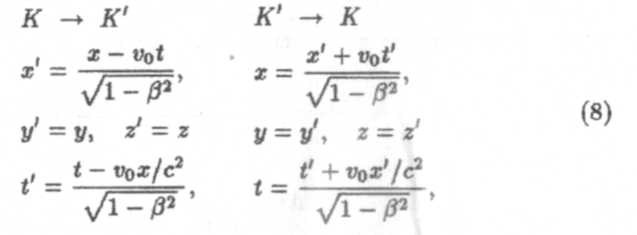
| ОпОперируя далее формулами (5) и (7), можно получить преобразования Лоренца длякоординат и времени в релятивистской механике |

т.е. отсчет времени в системах К я К' имеет относительный характер в отличие от случая классической механики, где время течет одинаково во всех инерциальных системах отсчета.
Найдем преобразование для координат и времени, предполагая, что хи tмогут быть линейными функциями только х'и t'и используя аналогию с преобразованием (1). Тогда
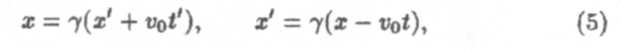
где τ — коэффициент пропорциональности, одинаковый вследствие равноправия систем К и К'. Л ал ее для определения величины τ обратимся к рассмотренному выше примеру, когда в начальный момент из начала координат систем К и К' посылается световой сигнал. Координаты
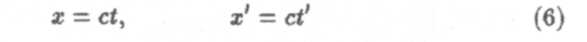
|
фиксированной точки Аможно выразить, используя преобразование (5):

|
Перемножая эти соотношения, получим
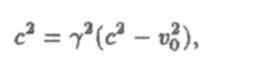
откуда
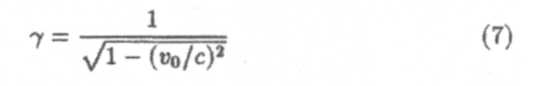
где β = v0/c. Преобразования Лоренца в случае малых скоростей (v0 « с) переходят в преобразования Галилея для классической механики. В этом заключается принцип соответствия. При v > с выражение (8) теряет смысл, и это согласуется с невозможностью движения при скоростях, больших скорости света.
Дата добавления: 2015-08-11; просмотров: 2801;
