Момента импульса
Скорость изменения момента импульса тела с течением времени равна моменту силы, действующей на тело
dL/dt = M (23)
Отсюда имеем: изменение момента импульса тела за промежуток времени dt равно импульсу момента силы за данный промежуток времени
dL = Mdt. (24)
Из формул (23), (24) следует, что если момент действующей силы М = 0, то момент импульса остается постоянным:
dL/dt = О, L = const. (25)
В этом случае систему можно рассматривать как замкнутую и сформулировать закон сохранения момента импульса:
Сумма моментов импульсов тел, составляющих замкнутую систему, есть величина постоянная.
Аналитически это записывается в виде:
L = const. I1ω1 + I2ω2 + I3ω3 + … + Inωn= const. (26)
Закон сохранения момента импульса является одним из фундаментальных законов природы. Он действует на всех структурных уровнях организации материи, как в макромире, так и в микромире. Многие элементарные частицы уже рождаются наделенные моментом импульса, который является такой же неотъемлемой характеристикой частицы, как ее масса или заряд. Внутреннее вращение элементарных частиц, благодаря которому часть из них обладает спином, является глубинным свойством нашего физического мира, до конца еще не понятым.
Практические приложения
закона сохранения момента импульса
Заметим, что эти приложения очень интересны, важны и чрезвычайно разнообразны. Мы остановимся только на некоторых из них. Для большей наглядности рассмотрим изолированную систему, состоящую из одного вращающегося тела. Тогда вместо (26) имеем I ω = const; отсюда следует, что при увеличении момента инерции тела угловая скорость уменьшается, и наоборот. Наиболее интересными в практическом плане являются гироскопы — массивные однородные тела, вращающиеся с большой угловой скоростью вокруг своей оси симметрии. Гироскопы применяются в различных навигационных приборах (гирокомпас, гирогоризонт). Другое важное применение гироскопов — поддержание заданного направления движения транспортных средств, например, судна (авторулевой) и самолета (автопилот). При всяком отклонении от курса вследствие каких-то воздействий положение оси гироскопа в пространстве сохраняется. Благодаря закону сохранения момента импульса не падают движущиеся мотоциклист и велосипедист, дальше и точнее стреляют нарезные орудия, ось вращения Земли сохраняет постоянное положение в пространстве.
Лекция №6
Гармонические колебания
Колебания очень широко распространены в природе и технике. Колебательным называется процесс, в котором какая-либо его характеристика последовательно отклоняется то в одну, то в другую сторону от положения равновесия. Колеблются температура воздуха, ствол и ветви дерева, вода в морях и океанах, автомобиль на рессорах, ток в грозовом разряде, магнитное поле Земли и т.д.
Колебания бывают периодическими и непериодическими. Непериодическое колебание можно разложить на периодические составляющие. Если возврат к положению равновесия совершается через равные промежутки времени, то колебание называется периодическим. Примером периодического движения может быть: движение маятника, движение ножей косилки, вибрация струны, суточные и годичные колебания температуры, отливы и приливы, биение сердца, дыхание, переменный ток, тепловое движение ионов кристаллической решетки и т.д. Из всевозможных периодических колебаний рассмотрим колебания гармонические, происходящие по закону синуса или косинуса.
Уравнение гармонического колебания
Рассмотрим равномерное движение материальной точки М по окружности радиуса R = А против часовой стрелки со скоростью ω (рис. 1).
При этом проекция N на вертикальный диаметр совершает колебания около положения равновесия О. Примем ОМ = А; ON = х — смещение в любой момент времени t, которое изменяется в пределах от +А до -А, совершая при этом периодические колебания.
Поэтому можно записать:
x = Asinφ (1)
но φ = ωt; ω = 2π/T = 2π/v. Получим и другие формы записи гармонического движения:
x = Asinωt, x = Asin 2π/T t, x = Asin 2πvt (2)
Если при t = 0 x ≠ 0, т.е. φ = φ0 ≠ 0, то уравнение гармонических колебаний примет более общий вид:
x = Asin(ωt + φ0).
Кинематические характеристики
гармонического колебательного движения
х — смещение материальной точки от положения равновесия в любой момент времени, измеряется в метрах.
А — амплитуда колебаний — максимальное отклонение точки от положения равновесия.
φ — фаза колебания, измеряется в радианах, tp = иЛ + <р0 — аргумент тригонометрической функции в уравнении гармонического колебания. Фаза определяет смещение в любой момент времени, т.е. определяет состояние колебательной системы. Изменение фазы на 2тг соответствует промежутку времени в один период - Г.
φ0 — начальная фаза колебания.
ω — циклическая частота, измеряется в рад/с.
T — период колебания (время одного полного колебания), измеряется в секундах.
v — частота колебания (число полных колебаний, совершаемых за единицу времени), измеряется в герцах: 1 Гц = 1/с = с-1.
Скорость гармонического колебания точки N (рис. 2). Скорость v колебания точки N определим как производную смещения (2) по времени:
v= dx/dt = x= ω A cos ω t = ω A sin (ωt + π/2).
Следовательно, скорость v тоже совершает гармонические колебания.
Ускорение гармонического колебания точки N (рис. 2)-. Поскольку скорость v зависит от времени t, то гармоническое колебание совершается с ускорением о, которое определим как производную скорости (3) по времени (или вторую производную смещения по времени)
a=dv/dt= ṽ =d2x/dt2 = ẍ= - ω2Asinωt = - ω2x
Следовательно, ускорение а тоже совершает гармонические колебания. ] Сопоставляя выражения для смещения, скорости и ускорения (формулы 1-4), приходим к следующим заключениям.
| t | X | V | а |
| ω А | |||
| T/4 | А | - ω2А | |
| T/2 | - ωА | ||
| ЗT/4 | -А | ш3А | |
| T | ωА |
а) И смещение (x), и скорость (v), и ускорение (а) совершают
гармонические колебания с одинаковой циклической часто-
той ω > (одинаковым периодом T = 2ir/ ω = 1/j/).
б) Амплитуды — разные (ф. 1-4), А — у смещения (x), ω А
у скорости (v), ω 2А — у ускорения (а).
в) Начальные фазы —разные. Колебание скорости (v) опережа-
ет колебание (х) на π/2 по фазе или на T/4 по времени.
φ=2π/T*t; ∆t =∆φ T/2π= π/2 * T/2π= T/4
Колебания ускорения (а) опережают колебания (г) на по фазе или на T/2 по времени: t = πТ/{2ω) = T/2. Представим эти заключения в виде таблицы (учитывая, что ω>t = (2π/T)t).
Сила, вызывающая гармонические колебания. При гармоническом колебании а = f(t) 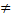 const, следовательно, гармоническое колебание вызывается переменной силой (F). Под ее действием материальная точка совершает гармоническое колебание с ускорением (a), следовательно:
const, следовательно, гармоническое колебание вызывается переменной силой (F). Под ее действием материальная точка совершает гармоническое колебание с ускорением (a), следовательно:
F = та = -тА ω 2 sin ω t = -mw3x = -kx, где k = m ω 2. (5)
F = -kx. Знак минус означает, что сила направлена противоположно смещению, т.е. эта сила стремится вернуть материальную точку в положение равновесия. Поэтому сила F называется возвращающей силой, а (к) — коэффициент возвращающей силы. Возвращающей силой может быть сила упругости, но может быть и квазиупругая сила, т.е. сила любой природы, величина которой прямо пропорциональна смещению из положения равновесия. Зная коэффициент А, можно найти циклическую частоту и период колебания.
к = т ω 2, ω = 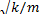 . (6)
. (6)
Учитывая, что ω = 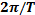 , получим формулу периода пружинного маятника
, получим формулу периода пружинного маятника
T= 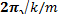 ,. (7)
,. (7)
Полная энергия гармонического колебательного движения. При гармоническом колебании происходят периодические взаимные превращения кинетической WK и потенциальной Wn энергии, обусловленной действием квазиупругой силы. Из этих энергий складывается полная энергия W колебательной системы:
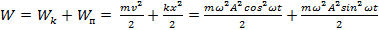 =
=
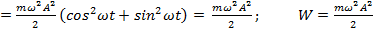 (8)
(8)
Полная энергия гармонического колебания постоянна и пропорциональна массе тела, квадрату циклической частоты и квадрату амплитуды колебаний.
Элементы теории колебания маятника
а) Физический маятник — твердое тело, совершающее периодические колебания относительно горизонтальной оси О под действием силы тяжести Р (ее составляющей F — возвращающей силы). Угол а отклонения маятника длиной l (l — расстояние от точки подвеса до центра масс маятника) от положения равновесия ОО мал: а < 8° = 0,14 рад. Считаем, что а > 0 вправо от оси ОО (рис. 3).
Тогда F = -Psin a = -mgsina 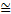 -mga =-mg x/l (9)
-mga =-mg x/l (9)
(знак минус, т.к. а — вправо, a F направлена влево). С другой стороны, рассматривая колебание как вращательное движение
массы (m) по дуге окружности, применим основное уравнение динамики вращения:
M = Iβ; Fl=Iβ или 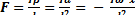 (10)
(10)
(а = βR = β1, см. лекцию № 5). Приравнивая правые части выражений (9) и (10), получим
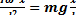 или
или 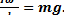
Отсюда ω= 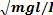 . Учитывая, что ω = 2/T, получим период колебаний физического маятника
. Учитывая, что ω = 2/T, получим период колебаний физического маятника
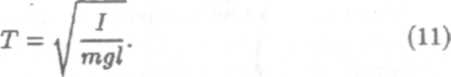
На практике часто физический маятник можно расматривать как математический.
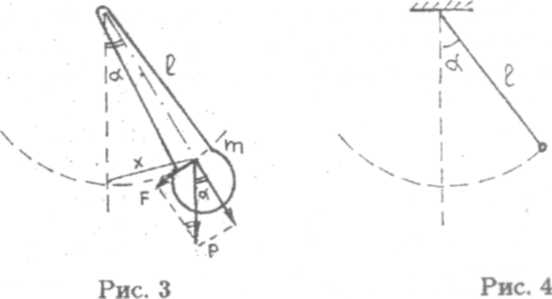
б) Математический маятник — материальная точка, колеблющаяся на невесомой и недеформируемой нити (рис. 4).
Лля материальной точки момент инерции математического маятника равен / = ml2, где тп — масса материальной точки, I — длина нити. Подставляя выражение момента инерции в формулу периода колебаний физического маятника (11), получим
Т =2π 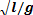 . (12)
. (12)
При малых отклонениях а период колебаний маятника пропорционален корню из его длины, обратно пропорционален корню из ускорения свободного падения и не зависит от массы маятника.

| Рис. 6 |
Рис. 5.
О затухающих колебаниях. Энергия гармонического колебания W ~ А2. Потеря на неизбежное трение ведет к постепенному уменьшению амплитуды и, наконец, к полному затуханию колебаний (рис. 5). Вся энергия колебания перейдет в теплоту и колебания прекратятся.
О вынужденных колебаниях. Чтобы сделать колебания незатухающими, надо восполнять потерю энергии, воздействуя на систему периодически изменяющейся силой f = f0 sinωвt, называемой вынуждающей (f0— амплитуда, ωB — круговая частота вынуждающей силы).
Такое колебание называется вынужденным. Оно происходит с частотой ωB (рис. 6). Определим амплитуду вынужденных колебаний, пренебрегая трением и считая, что на тело действует только вынуждающая сила f и возвращающая сила F = -тω2х.
F + f = ma = -тωв2х или -тω2х + f0 sinωвt = -тωв2х
Откуда
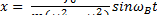
Следовательно, амплитуда
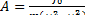 (13)
(13)
Амплитуда зависит от соотношения ω и ωв. При ωв → ω будет А → ∞ (однако, наличие трения этого не допускает). Резкое возрастание амплитуды колебаний при ω→ ωв называется явлением резонанса. Посредством резонанса можно небольшой вынуждающей силой вызвать сильные колебания системы (часы на нити, мост при строевом шаге и т.п.).
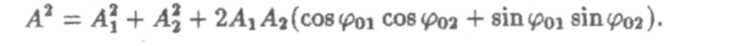
Лекция №7
Сложение гармонических колебаний
1. Сложение гармонических колебаний одного направления. Пусть тело одновременно участвует в двух одинаково направленных колебаниях одинаковой циклической частоты, описываемых уравнениями
x1=A1sin(ωt + φ01), (1)
x2=A1sin(ωt + φ02), (2)
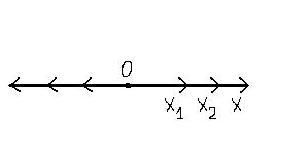
очевидно (рис. 1), что
x = x1 + x2 или (3)
x=Asin(ωt + φ0), (4)
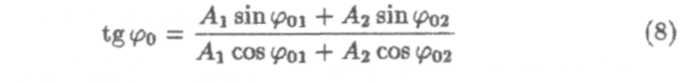 Необходимо определить амплитуду А результирующего колебания и начальную фазу φ0. Применяя формулу преобразования синуса суммы и подставляя в (3) выражения (4), (1), (2), получим
Необходимо определить амплитуду А результирующего колебания и начальную фазу φ0. Применяя формулу преобразования синуса суммы и подставляя в (3) выражения (4), (1), (2), получим
Asin ωt * cos φ0 + Acos ωt *sin φ0 = A1sin ωt * cos φ01 + A1cos ωt *sin φ01+
+ A2sin ωt * cos φ02 + A2cos ωt *sin φ02
приведя подобные,
Asin ωt * cos φ0 + Acos ωt *sin φ0 = (A1 cos φ01 + A2 cos φ02)sin ωt + (A1 sin φ01+ A2 sin φ02) cos ωt.
Очевидно, что равенство будет тождественно выполняться при условии равенства коэффициентов при sinurt правой и левой частей и коэффициента при cos ωt правой и левой частей:
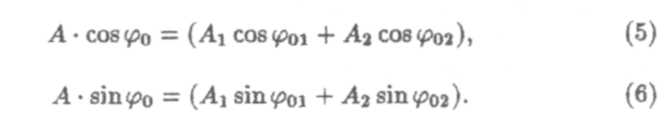
Возводя в квадрат и складывая формулы (5) и (6), получим
Вспомнив формулу соs(а ±β) — соsа • cosβ±sina • sinβ, получим
— формула амплитуды результирующего колебания. Поделив равенство (6) на равенство (5), получим
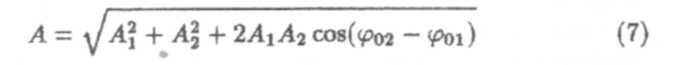
— формула для начальной фазы результирующего колебания.
2. Частные случаи
а) Циклическая частота и начальные фазы одинаковы, амплитуды различны
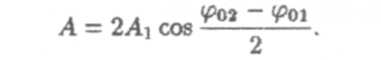

 Тогда из выражений (8) и (7) следует, что
Тогда из выражений (8) и (7) следует, что

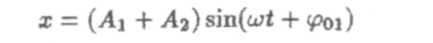
В этом случае уравнение результирующего колебания примет вид
или, поскольку начальные фазы всех колебаний одинаковы,
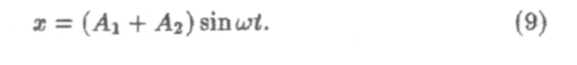
б) Циклическая частота и амплитуды одинаковы, канальные фазы различны
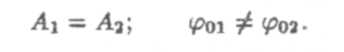
 Тогда из выражений (8) и (7) получим
Тогда из выражений (8) и (7) получим
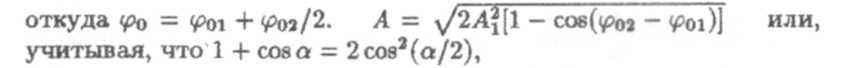
В этом случае уравнение результирующего колебания будет
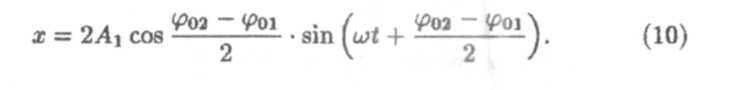
При φ02 - φ01=0, 2π, 4π…2nπ, где п = 0,1,2,3,.. А= 2A1 — амплитуда максимальна. При φ02 - φ01— π, 3π, 5π…(2n+1)n A =0 — колебания взаимно гасятся.
3. Сложение двух взаимно перпендикулярных гармонических колебаний
Пусть тело одновременно участвует в двух взаимно перпендикулярных колебаниях одинаковой циклической частоты, описываемых уравнениями
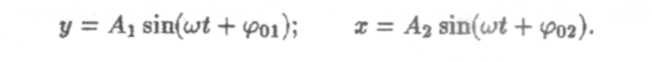 Надо найти уравнение траектории у = f(x)y исключив из уравнений слагаемых колебаний время t. Разделив каждое уравнение почленно на соответствующую амплитуду и применив формулу синуса суммы, получим
Надо найти уравнение траектории у = f(x)y исключив из уравнений слагаемых колебаний время t. Разделив каждое уравнение почленно на соответствующую амплитуду и применив формулу синуса суммы, получим
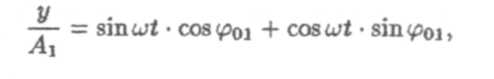
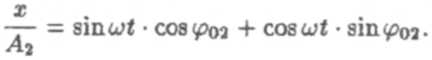
 Выполним с последними уравнениями следующие преобразования. Домножим первое и второе равенство на cos φ01 и cos φ02 соответственно и вычтем их друг из друга. Аналогичным образом домножим исходные равенства на sin φ02 и sin φ01 и снова вычтем. В результате получим два новых уравнения
Выполним с последними уравнениями следующие преобразования. Домножим первое и второе равенство на cos φ01 и cos φ02 соответственно и вычтем их друг из друга. Аналогичным образом домножим исходные равенства на sin φ02 и sin φ01 и снова вычтем. В результате получим два новых уравнения
Возводя эти равенства в квадрат и складывая, получим
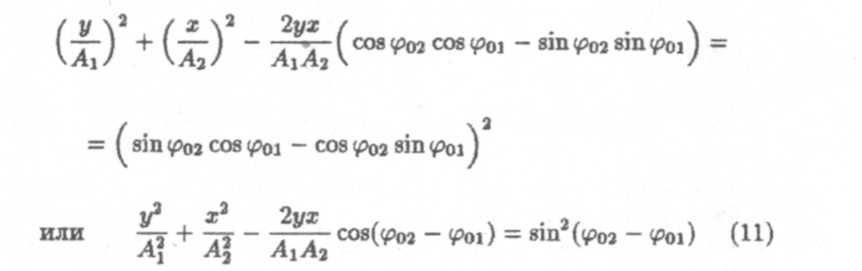
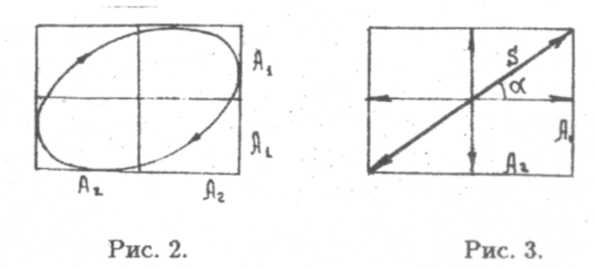
 — это уравнение эллипса, вписанного в прямоугольник со сторонами 2A1 и 2А2 (рис. 2). В результате материальная точка будет двигаться по атому эллипсу по часовой или против часовой стрелки (в зависимости от разности фаз).
— это уравнение эллипса, вписанного в прямоугольник со сторонами 2A1 и 2А2 (рис. 2). В результате материальная точка будет двигаться по атому эллипсу по часовой или против часовой стрелки (в зависимости от разности фаз).
4. Частные случаи
а) Начальные фазы одинаковы, амплитуды различные

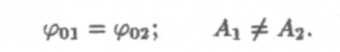
Тогда из формулы (11) следует
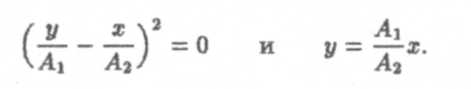
|
Это уравнение прямой, т.е. результирующее колебание происходит по наклонной прямой 5, проходящей через положение
равновесия под углом а к направлению колебания х (рис. 3), tga = A1/A2.
Результирующее смещение 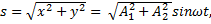 где
где  амплитуда результирующего колебания; тогда
амплитуда результирующего колебания; тогда 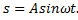
б) начальные фазы различаются на ж/2, амплитуды различные
тогда из (11) получим
Это уравнение эллипса. Следовательно результирующее движение материальной точки совершается по эллипсу, полуоси которого равны амплитудам слагаемых колебаний (рис. 4). Если A1= А2 = А, то у1 + х2 = А2, т.е. движение происходит по окружности радиусом А.
Направление движения по эллипсу определяется следующим образом. Если φ01 = φ02 +π/2, то уравнения слагаемых колебаний примут вид
При t = 0 и у = 0, а. х = A2, т.е. материальная точка находится в положении (1) (рис. 4 и 5). С ростом t у— будет расти, а x — уменьшается, что соответствует движению против часовой стрелке. Если φ02 = φ01 +3π/2, nj
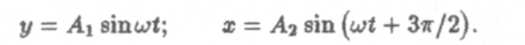

 При t = 0 и у = 0, а. х = - A2,т.е. материальная точка находится в положении 2 (рис. 5). С ростом t, у— увеличивается, а x — уменьшается, что соответствует движению по часовой стрелке.
При t = 0 и у = 0, а. х = - A2,т.е. материальная точка находится в положении 2 (рис. 5). С ростом t, у— увеличивается, а x — уменьшается, что соответствует движению по часовой стрелке.
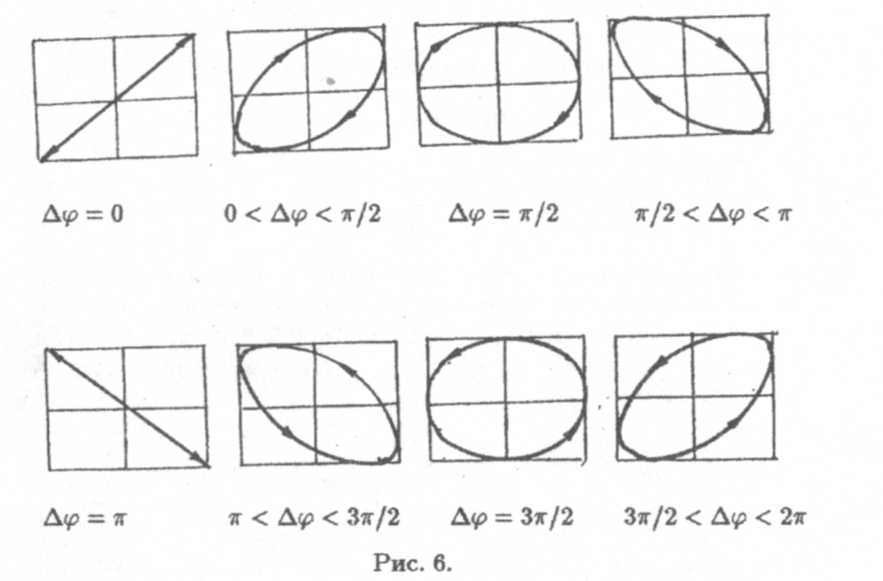
Зависимость характера результирующей траектории от разности фаз ∆φпредставлена на рис. 6.
Если гармонические колебания совершаются под углом а (а ≠π/2), то проведя две взаимно перпендикулярные оси, одна из которых совпадает с гармоническим колебанием 2 (рис. 7), разложим затем гармоническое колебание 1 на два составляющих 1' и 2' по этим осям.
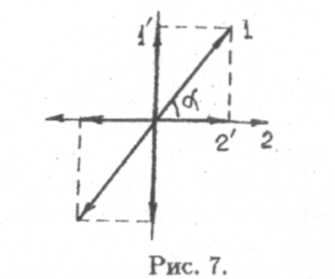
Тогда задача сведется к сложению двух однонаправленных гармонических колебаний 2 и 2' и затем сложению результирующего гармонического колебания с перпендикулярным гармоническим колебанием 1'.
Умея складывать два любых гармонических колебания, можно сложить и любое их число.
Лекция № 8 Волны
Волной называется процесс распространения колебаний в пространстве. Волны принято подразделять на продольные и поперечные.
Продольной называется такая волна, у которой колебания совершаются в направлении распространения волны. Примером являются звуковые волны в газах и жидкостях, часть волн в упругих средах. Поперечной называется волна, у которой колебания происходят в направлении, перпендикулярном по отношению к направлению распространения волны. Примером являются световые волны, волны на поверхности воды, часть волн в упругих средах.
Монохроматической (гармонической) называется волна, у которой колебания в зависимости от времени происходят по закону синуса или косинуса;
 Здесь з — величина, колебания которой мы рассматриваем (например, колебания давления для звуковой волны или колебания напряженности электрического поля в электромагнитной волне и т.п.); А — амплитуда колебаний, φ(t, у, z)= ωt + φ1(х, у, z) — фаза колебаний. В случае произвольной зависимости от времени волновое возмущение можно представить как суперпозицию гармонических колебаний.
Здесь з — величина, колебания которой мы рассматриваем (например, колебания давления для звуковой волны или колебания напряженности электрического поля в электромагнитной волне и т.п.); А — амплитуда колебаний, φ(t, у, z)= ωt + φ1(х, у, z) — фаза колебаний. В случае произвольной зависимости от времени волновое возмущение можно представить как суперпозицию гармонических колебаний.
 Фазовым фронтом называется геометрическое место точек в пространстве, колеблющихся в одинаковой фазе
Фазовым фронтом называется геометрическое место точек в пространстве, колеблющихся в одинаковой фазе
При фиксированном моменте времени t = const это требование сводится к условию 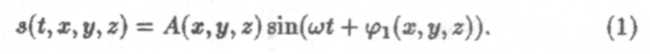 :
:

Плоской волной называется волна, у которой фазовый фронт является плоскостью. Наряду с плоскими, можно рассматривать и другие формы волновых фронтов, например, сферические, цилиндрические и т.п. Однако любую другую волну можно представить как суперпозицию плоских волн.
Лучом называется траектория, по которой движется волновое возмущение в среде. Лучи ориентированы перпендикулярно по отношению к фазовым фронтам. В случае однородной среды для плоской волны лучи являются прямыми линиями. В случае плоской монохроматической волны, распространяющейся вдоль оси х, уравнение (1) принимает вид:
Здесь ω — циклическая частота волны, к = ω/св— волновое число, св— скорость распространения волны (фазовая скорость), φ0 — начальная фаза. Имеют место также соотношения: Т = 2п/φ — период колебаний волны, λ = св• Т — длина волны, к = 2π/λ.
Соотношение (4) называется уравнением бегущей волны. Знак " -" соответствует волне, бегущей в положительном направлении оси х, а знак " +" волне, бегущей в отрицательном направлении оси а;. Уравнение, описывающее поверхность равной фазы, в этом случае можно записать в форме:
Дифференцируя (5) по времени, имеем;

Отсюда

Знаки "+" и "-" соответствуют волнам, бегущим в положительном и отрицательном направлениях оси х.Дифференциальное волновое уравнение, соответствующее (4), имеет вид:

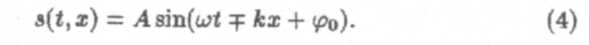
Вывод этого уравнения для электромагнитных волн дан нами в лекции № 31.
Волны называются когерентными, если разность фаз этих волн в любой точке пространства не зависит от времени. При сложении когерентных волн, поляризованных вдоль одинаковых направлений, наблюдается явление интерференции, т.е. взаимного усиления и ослабления волн. В некоторой точке волны максимально усиливают друг друга, если разность фаз между волнами равна нулю (или четному числу π рад). Волны также максимально ослабляют друг друга, если разность фаз в данной точке равна π (или нечетному числу π рад). Подробнее явление интерференции рассмотрено в лекции № 33.
Распространяясь в пространстве с течением времени, волны переносят энергию. Рассмотрим, как рассчитать поток энергии, связанный с волнами различных типов.
Упругие волны. В этом случае атомы упругой среды (например, металла) совершают гармонические колебания. Полная энергия одного колеблющегося атома равна
где m — масса атома, vmax— амплитуда скорости при колебательном движении атома, ω — циклическая частота колебаний, А— амплитуда смещения. Если концентрация атомов равна n, то очевидно, что полная энергия, связанная с колебательным движением частиц среды, заключенная в единице объема, равна:
Здесь р = пт— плотность среды. Тогда очевидно, что энергия, переносимая волной в единицу времени через единицу площади поверхности, расположенной перпендикулярно направлению распространения волн, определяется модулем вектора Умова:
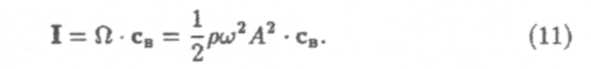
Величина |I| также называется интенсивностью волны. Вектор сB ориентирован в направлении распространения волны.
Электромагнитные волны. В этом случае плотность энергии электромагнитного поля, связанного с волной, определяется по формуле 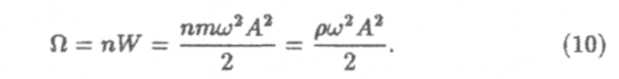
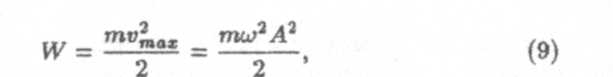 :
:
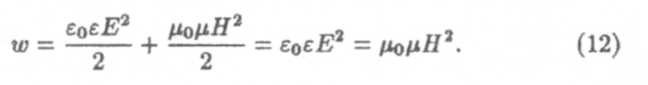
Здесь Е— напряженность электрического поля волны, H — напряженность магнитного поля волны, ε0 — электрическая постоянная, μ0— магнитная постоянная, ε — диэлектрическая проницаемость вещества, μ— магнитная проницаемость вещества.
Энергия, связанная с электрическим и магнитным полем волны, одинакова: (ε0εЕ2/2 = μ0μН2/2). Из (12) следует, что
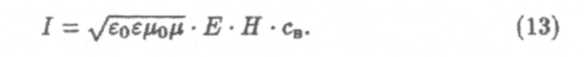
Учитывая, что  (см. лекцию № 31) и то, что
(см. лекцию № 31) и то, что 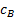 — перпендикулярна как к Е,так и к Н,найдем
— перпендикулярна как к Е,так и к Н,найдем

Этот вектор называется также вектором Умова-Пойнтинга. Он, согласно (14), определяется с помощью векторного произведения векторов Eи Н.
Электромагнитные волны, как и любые другие физические волны, производят давление на встречающиеся на их пути препятствия, поглощающие и отражающие эти волны. Давление электромагнитных волн объясняется тем, что под влиянием электрического поля волны заряженные частицы вещества приходят в упорядоченное движение и подвергаются со стороны магнитного поля волны действию сил Лоренца.
Дата добавления: 2015-08-11; просмотров: 1805;
