Зависимость между главными моментами, вычисленными относительно различных центров приведения
Выберем в теле два центра приведения 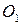 и
и 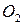 . Запишем выражения для главных моментов относительно этих центров
. Запишем выражения для главных моментов относительно этих центров

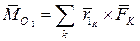 ,
, 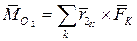
Из рисунка видно, что радиус-векторы точек приложения произвольной силы 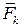 относительно этих центров связаны выражением
относительно этих центров связаны выражением
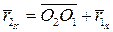
Подставляя его в выражение для второго главного момента, получим
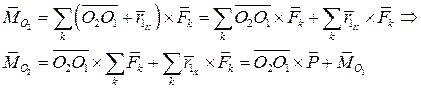
Таким образом, главный момент системы сил относительно второго центра равен главному моменту относительно первого центра плюс момент главного вектора, приложенного к первому центру, относительно второго центра.
Инварианты системы сил
Инвариантами называются векторные или скалярные параметры, которые не зависят от преобразования координат. В системе сил, как мы видим, таким параметром является главный вектор. Его называют векторным инвариантом системы сил. Главный момент инвариантом не является, так как он различен для различных центров приведения. Однако инвариантом служит скалярное произведение главного вектора на главный момент. В самом деле

Отсюда также вытекает, что инвариантом является и проекция главного момента на направление главного вектора
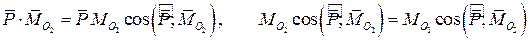
Дата добавления: 2015-08-08; просмотров: 3996;
