Условия равновесия произвольной системы сил

Геометрические условия равновесия, как это видно из предыдущего пункта, соответствуют двум векторным уравнениям

,

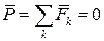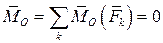
Проектируя эти уравнения на оси декартовой системы координат, получим шесть независимых уравнений равновесия

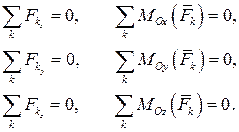
Таким образом, для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы равнялись нулю суммы проекций всех сил на выбранные координатные оси и суммы моментов всех сил относительно этих осей.

Различные типы систем сил и условия их равновесия:

· пространственная система сходящихся сил. Выбираем начало координат совпадающее с точкой пересечения линий действия сил, входящих в рассматриваемую систему. Момент каждой из этих сил относительно любой оси, проходящей через начало отсчёта (пересекаемой линией действия силы), равен нулю. Поэтому три из шести уравнений равновесия выполнятся тождественно и условиями равновесия в этом случае будут:

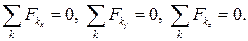
· пространственная система параллельных сил. Выбираем систему координат так, чтобы одна из осей (например, 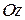) была направлена параллельно силам. Проекции сил на ос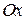и и 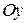равны нулю, момент любой из сил, параллельной оси, относительно этой оси равен нулю. Поэтому из шести уравнений равновесия получаем три условия:

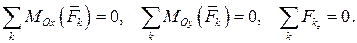
· произвольная плоская система сил. Совместим одну из координатных плоскостей (например ) с плоскостью действия сил, тогда, очевидно, будут тождественно равными нулю следующие параметры произвольной силы:

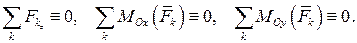
Поэтому условия равновесия запишутся в виде трёх уравнений:

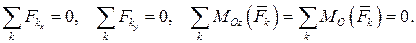
Теорема о моменте равнодействующей (теорема
Вариньона)

Векторный момент равнодействующей рассматриваемой системы сил относительно любой точки равен сумме векторных моментов всех сил этой системы относительно той же точки.

Иными словами, если 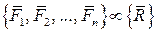, то

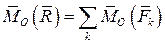
Для плоской системы сил данная теорема запишется в виде алгебраических моментов относительно произвольной точки на плоскости

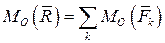
Эта теорема широко применяется в вычислениях моментов сил при решении практических задач.