Методика решения задач на равновесие пространственной системы сил

Любая задача статики изучаемого курса может быть решена по следующему плану:

· выделить тело (элемент) или систему тел, равновесие которых будем рассматривать (использование аксиомы освобождения от связей);

· расставить силы, действующие на выделенные элементы. Т. к. кроме активных сил на выделенные элементы действуют реакции отброшенных связей, то этот пункт существенно зависит от первого и, обычно, выполняется вместе с ним;

· дать анализ полученной системы сил, выяснить, является ли задача статически определённой;

· записать условия равновесия и произвести над ними действия с целью определения неизвестных;

· дать анализ полученного ответа.

РАСПРЕДЕЛЁННЫЕ СИЛЫ

До сих пор рассматривались силы, приложенные в одной точке, которые называются сосредоточенными. В действительности взаимодействие одного тела с другим осуществляется либо по некоторой площадке, либо по объёму тела. Пример поверхностных сил — давление воды на стенку плотины, объёмных — силы тяжести — они распределены по всему объёму тела, но часто, для удобства, мы заменяем эти силы их равнодействующей, приложенной к центру тяжести.

Распределённые силы характеризуются интенсивностью и направлением действия. Интенсивностью распределённой силы называется величина силы, приходящаяся на единицу объёма, площади или длины линии.

Силы принимаются распределёнными по линии в том случае, когда размерами тела в поперечном направлении можно пренебречь по сравнению с его длиной. Такие тела называются стержнями или балками. Распределёнными, обычно, бывают параллельные или сходящиеся силы, однако, распределёнными могут быть и пары сил.

Рассмотрим вопросы замены распределённых сил сосредоточенными силами. Пусть силы распределены по отрезку АВ, длиной L. Разобьём весь отрезок AB на элементарные участки 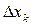. На каждый из них действует сила равная 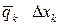, т. к. из-за малости участка интенсивность в его пределах можно считать постоянной. Суммируя элементарные силы, найдём равнодействующую. Величина её равна главному вектору

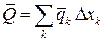
При устремлении к нулю элементарной длины 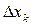сумма сил перейдёт в интеграл

.

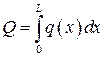Точка приложения равнодействующей силы определяется с помощью теоремы Вариньона:

,

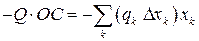или при предельном переходе

Откуда окончательно