Частные случаи приведения системы сил к центру

Исходя из рассмотрения скалярного инварианта, все случаи приведения системы сил можно классифицировать следующим образом:

При равенстве нулю скалярного инварианта:

· Главный вектор не равен нулю ( 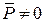), а главный момент равен нулю ( 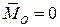). Система приводится к равнодействующей, равной главному вектору;

· Главный вектор равен нулю ( 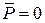), а главный момент не равен нулю ( 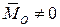). Система приводится к паре сил с моментом, равным главному моменту системы;

· Главный вектор и главный момент не равны нулю ( 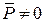, 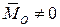), но угол между ними равен 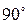. В этом случае возможно дальнейшее упрощение

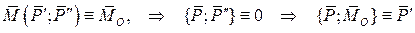
Система приводится к равнодействующей силе, но линия её действия отстоит от первоначального центра приведения на расстоянии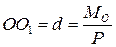

· Главный вектор и главный момент равны нулю. Система уравновешена:

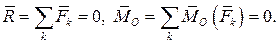
В случае, когда скалярный инвариант не равен нулю, полезно рассмотреть следующие варианты приведения сил:

Угол между главным вектором и главным моментом равен 0 или 180°. Такая комбинация главного вектора и главного момента называется динамой или динамическим винтом. Линия, вдоль которой действуют оба вектора называется осью динамы.

Угол между главным вектором и главным моментом произволен. В этом случае возможно упрощение

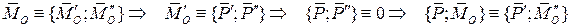
В этом случае система приводится к динаме, ось которой отстоит от первоначального центра приведения на расстоянии

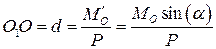
Сведём все случаи, рассмотренные выше, в таблицу:

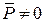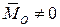
	,	Равнодействующая
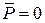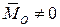
	,	Пара сил
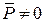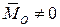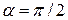
	, ,	Равнодействующая
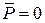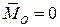
	,	Равновесие
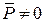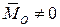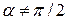
	, ,	Динама