Кинетическая энергия вращающегося тела

Обратимся опять к рисунку 7. Пусть теперь тело вращается вокруг оси с угловой скоростью 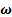= | |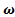. Тогда очевидно, что кинетическая энергия i-ой материальной точки

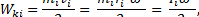
где v_i = 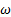r_i. Суммируя по всем материальным точкам, соста­вляющим тело, имеем

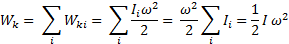
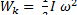(19)

Формула (19) описывает кинетическую энергию тела с непо­движной осью вращения. Если же тело одновременно участвует как в поступательном, так и во вращательном движениях, его кинетическая энергия равна сумме кинетических энергий, свя­занных с этими движениями

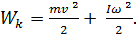(20)

Здесь v — скорость движения центра масс тела.

Момент импульса

По аналогии с импульсом при поступательном движении при вращательном движении вводится момент импульса тела:

L = I_* . (21)

Для материальной точки имеем (рис. 8)

L = г _* р = mr _* v. (22)

Момент импульса материальной точки равен векторному про­изведению радиус-вектора положения точки на импульс этой материальной точки.

При изучении вращательного движения становится очевид­ной аналогия многих, если не всех, характеристик этого дви­жения и движения поступательного. Для наглядности выпол­ним сопоставление аналогичных физических величин и законов в виде таблицы.

Таблица аналогий между

поступательным и вращательным движением

Поступательное движение Вращательное движение

S, S – путь, перемещение φ, φ–угол повората

v, v – скорость ω, ω – угловая скорость

a, a – ускорение β, β – угловое ускорение

S = S₀ +v₀t + at²/2 – путь φ = φ₀ + ω₀t + βt² – угол

при равноуск. движении пов. При равноуск. Вращении

v = v₀ +at - скорость ω = ω₀ + βt - угловая скорость

при равноуск. Движении При равноуск. Вращении

m – масса тела I – момент инерции

F – сила M – момент силы

p = mv – импульс L = I ω – момент импульса

dp/dt = F – 2 закон Ньютона dL/dt = M – аналог 2 закона Н.

dp= F _* dt dL= M_* dt

закон изменения импульса закон изменения момента имп.

dA = F _* dS – работа dA= M _* dφ - работа

N = F _* v – мощьность N = M _*ω – мощьность

M₁v₁ + m₂v₂ = const I₁ω₁ + I₂ω₂= const

Закон сохранения импульса Закон сох. момента импульса

W_k = mv²/2 – кинет. Энергия W_k = I ω ²/2 – кинет. Энергия