Энергия. Энергия — важнейшая величина, характеризующая состояние системы, способность системы совершать работу
Энергия — важнейшая величина, характеризующая состояние системы, способность системы совершать работу, переходя из одного состояния в другое.
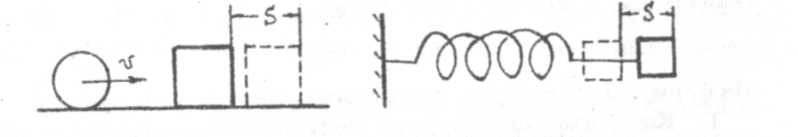
Рис.4 Рис.5
Например, катящийся шар, сталкиваясь с некоторым телом, переместит его и, следовательно, совершит работу. Значит, катящийся шар обладает энергией (рис. 4). Растянутая пружина, сокращаясь, будет перемещать свои витки (или другое тело) и, следовательно, совершит работу (рис. 5). Тело, приподнятое над землей на некоторую высоту, будучи освобожденным от связи, начинает падать, т.е. перемещаться и, следовательно, совершать работу. Значит оно обладает энергией (рис. 6).
Отметим, что шар, тело и пружина обладают энергией независимо от того, совершают они в данный момент работу или нет. Важно, что они обладают способностью совершать работу.
Обычно за конечное состояние системы принимают такое, в котором она уже не может совершать работу за счет данного вида энергии.
Из приведенных примеров видно, что если механическая энергия связана с движением системы или ее частей, то это кинетическая энергия {WK). Если энергия связана с взаимоположением тел или частей одного и того же тела, то это потенциальная энергия (Wn).
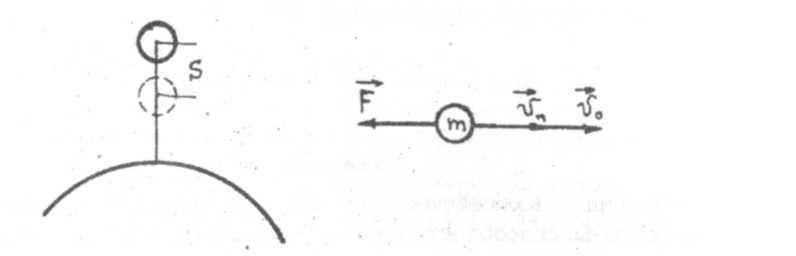
Рис. 6. Рис.7
Работа, совершаемая системой при переходе из одного состояния в другое, равна разности энергий системы в исходном (начальном) и конечном состояниях
A =Wo — Wn. (1)
Из формулы (1) следует, что энергия измеряется в джоулях.
1. Кинетическая энергия поступательно движущегося тела. Пусть под действием тормозящей силы F тело массой т замедлило на пути S свою скорость от оо До v„, имея ускорение о в течение промежутка времени t (рис. 7).
Тогда можно записать, что
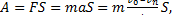 где
где 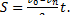
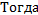
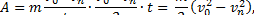
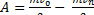 . (2)
. (2)
Сопоставляя формулы (1) и (2), получим выражение кинетической энергии тела
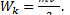 (3)
(3)
По формуле (3) определяется кинетическая энергия в классической механике, а релятивистское выражение для кинетической энергии определяется формулой (3а)
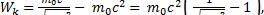 (3a)
(3a)
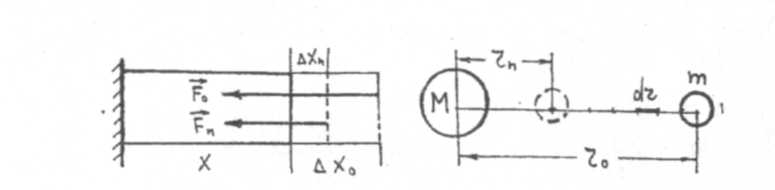
Рис. 8. Рис.9.
где то — масса тела, покоящегося относительно наблюдателя (масса покоя); » — скорость движения тела, значение которой соизмеримо со скоростью света (с), с = 299793 км/с 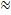 3-108 м/с.
3-108 м/с.
2. Потенциальная энергия упруго деформированного тела. Пусть упруго деформированный стержень растянулся (удлинился) на величину  х при первоначальной длине х (рис. 8).
х при первоначальной длине х (рис. 8).
После устранения деформирующей силы сила упругости начнет укорачивать стержень. Пусть это укорочение совершилось от деформации  х0 при силе упругости F0 до деформации
х0 при силе упругости F0 до деформации  хn, при силе Fn. Тогда работа силы упругости
хn, при силе Fn. Тогда работа силы упругости
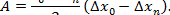
По закону Гука F = 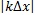 . Поэтому
. Поэтому 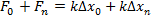 =
=
=k( 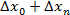 ) и
) и
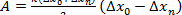 или
или  (4)
(4)
После сравнения (4) и (1) получим выражение потенциальной энергии
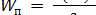 . (5)
. (5)
3. Потенциальная энергия тела в гравитационном поле.
Пусть тела массой М и т (рис. 9) взаимно притягиваются по закону всемирного тяготения так, что переместятся от расстояния г0 до г».
Разобьем перемещение на бесконечно малые отрезки dr и определим работу на одном таком отрезке:
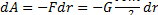
Знак минус объясняется тем, что dA > 0 (система сама совершает работу), a dr < 0 (расстояние уменьшается).
Тогда вся работа

| Рис. 10. Рис. 11. |
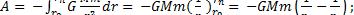
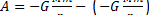 . (6)
. (6)
Сравнивая равенство (6) с формулой (1), имеем выражение потенциальной энергии в поле тяготения
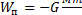 . (7)
. (7)
При г = 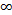 Wn = 0 — это максимум, так как с уменьшением г энергия Wa будет тоже уменьшаться.
Wn = 0 — это максимум, так как с уменьшением г энергия Wa будет тоже уменьшаться.
4. Потенциальная энергия тела, приподнятого над землей. Рассмотрим тело, приподнятое на небольшую высоту над землей h < R (рис. 10) (М — масса Земли, Я — ее радиус).
Согласно формуле (6),
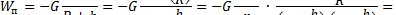
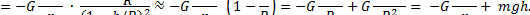
В "земных" задачах потенциальную энергию W„ = -GMmjR обычно принимают за начало отсчета, так как дальнейшее сближение тела т с Землей невозможно. Тогда
Wп = mgh. (8)
5. Закон сохранения и превращения энергии. В природе и технике повсеместно происходит превращение энергии из одних видов в другие: механической в электрическую (машинный генератор тока), электрической в световую (лампа накаливания) и т.п. Но опыт показывает, что полная энергия изолированной системы остается при этом постоянной
Wполн = const. (9)
Итак, энергия может переходить из одних видов в другие, но полная энергия изолированной системы остается постоянной — закон сохранения и превращения анергии.
При всех происходящих в природе процессах энергия не исчезает и не возникает вновь, а лишь передается от одних материальных объектов к другим, превращаясь из одной формы в другую в равных количествах.
В механике происходит превращение кинетической энергии в потенциальную, и наоборот. В силу своей всеобщности закон сохранения не выводится в общем виде, но может быть подтвержден любым конкретным процессом (см. рис. 11).
Рассмотрим, например, случай падения тела с некоторой высоты на землю. Запишем полную энергию тела в первом и втором состояниях (на высотах h1 и h2 соответственно).
W1=Wn1+Wk1=mgh1+0= mgh1 ,
W2=Wn2+Wk2=mgh2+ 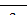 , v2=2g(h1-h2),
, v2=2g(h1-h2),
W2= mgh2 +  2g(h1-h2)= mgh2+mgh1 - mgh2 = mgh1.
2g(h1-h2)= mgh2+mgh1 - mgh2 = mgh1.
Видим, что W1 = W2 всегда, поскольку состояние (2) взято произвольно.
Закон сохранения и превращения энергии раскрывает физический смысл понятий энергии и работы. Рассматривая движение материи в широком смысле этого слова как всякий процесс, всякое изменение материи (а не только ее механическое перемещение), можно сказать, что энергия есть количественная и качественная характеристика различных форм движения материи, о работа — количественная характеристика превращения одних форм движения материи в другие.
Таким образом, работа и энергия — различные физические величины, хотя они выражаются в одинаковых единицах (джоулях): [A] = [W] = Дж.
Лекция №5
Вращательное движение твердого тела
Вращательным называется такое движение твердого тела, при котором все его точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.
Момент инерции тела
Моментом инерции материальной точки относительно оси ОО' называется скалярная физическая величина, равная произведению массы материальной точки т на квадрат расстояния г до оси (рис. 1)
I= mr2. (1)
Момент инерции тела I равен сумме моментов инерции Ij составляющих его материальных точек (рис. 2)
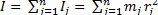 (2)
(2)
Здесь п — число материальных точек, составляющих тело.

Если n 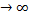 , а масса каждой из материальных точек тj
, а масса каждой из материальных точек тj  , то сумма в формуле (2) заменяется интегралом по объему тела
, то сумма в формуле (2) заменяется интегралом по объему тела
 (3)
(3)
Здесь  — плотность тела.
— плотность тела.
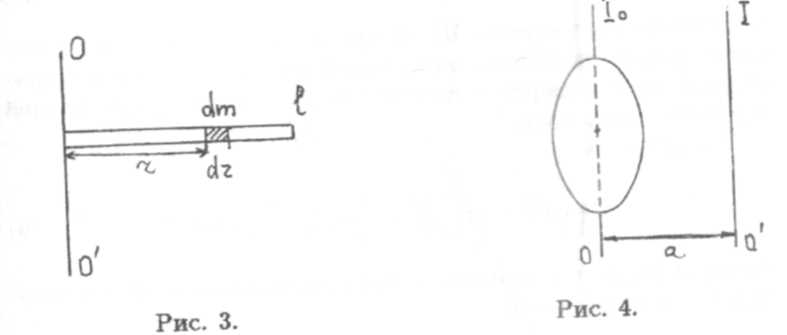
Пример. Вычисление момента инерции стержня относительно оси, проходящей через его конец перпендикулярно к стержню
Пусть т - масса стержня, l - его длина, т/l - линейная плотность стержня, т.е. масса, приходящаяся на единицу длины стержня. Тогда имеем dm = {m/l)dr (рис. 3).
 .
.
Аналогичные расчеты моментов инерции других тел относительно оси, проходящей через центр масс тела дают
I=mR2/2 – для диска и цилиндра радиуса R, (5)
I=2mR2/5 – для шара радиуса R, (6)
I=ml2/12 – для стержня длиной l (7)
Как показывают приведенные формулы, момент инерции тела зависит от его массы m размера тела г или формы тела (шар или цилиндр) и положения оси.
Дата добавления: 2015-08-11; просмотров: 1141;
