Динамики вращательного движения

(аналог второго закона Ньютона)

Рассмотрим вращение твердого тела вокруг закрепленной оси, проходящей через тело. Тогда имеем:

Угловое ускорение твердого тела прямо пропорционально мо­менту силы, действующей на тело, и обратно пропорционально моменту инерции этого тела

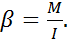(14)

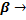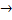Если в формуле (14) произвести замену а, М F, I 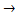т, то очевидно получим второй закон Ньютона в его классической формулировке. Формула (14) показывает, что момент инерции тела описывает инертные свойства тела при вращательном дви­жении.

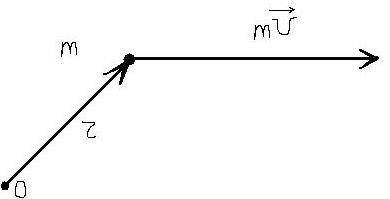
Выведем формулу (14). Рассмотрим силу F_i, действую­щую на одну из i-ых материальных точек, составляющих те­ло (рис. 7). Разложим эту силу на три составляющих F_i = 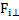+ F_iвр + F_i||. Здесь 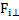— параллельна оси, 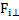— перпен­дикулярна оси и проходит через ось, F_iвр — перпендикуляр­на двум другим составляющим и, следовательно, плоскости ри­сунка. Очевидно, что именно последняя из рассмотренных со­ставляющих и будет вращать материальную точку вокруг оси. Применяя второй закон Ньютона, получим

F_iвр = m_ia_i (15)

Умножая (15) слева векторно на г_iи учитывая, что а_i- = 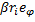, г_i= r_ie_i, где 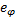— единичный вектор, направленный по каса­тельной к окружности, по которой движется материальная точ­ка, е_r — единичный вектор в направлении r_i , найдем

М_i = r_i* F_iвр = m_ir_{i *} а_i = 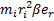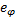_* = I_{i *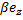} . (16)

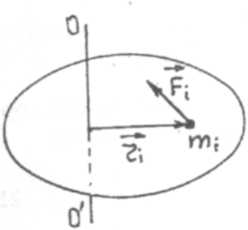
Здесь I_i — момент инерции материальной точки. Поскольку в нашем случае вектор 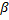направлен вдоль оси ОО' (ось z), то (16) можно переписать в форме:

М_i=I_i .(17)

Рис. 7. Рис. 8.

Выполнив в (17) суммирование по всем точкам материального тела, получаем

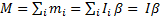(18)

Очевидно (18) дает другую форму записи основного закона (14).