Следствия из преобразований Лоренца
1. Относительность одновременности событий. Из преобразований Лоренца вытекает, что если два независимых события происходят в системе К в один и тот же момент времени (t1 = t2)ив одном месте (х1 = х2), то в системе К' эти события также будут происходить в одной точке (х'1 = х'2) и одновременно (t'1 = t'2). В том случае, когда события в системе К разобщены (х1 ≠ х2), но одновременны (t1 = t2),в системе К'эти независимые события разобщены (х'1 ≠ х'2)и неодновременны (t'1 ≠ t'2).
2. Относительность длительности событий (промежутков времени). Пусть в системе К’в одной точке х'1 = х'2 =a происходит событие, длительность которого ∆τ = t'1 = t'2.Согласно
преобразованию Лоренца (8) для времени в системе Кэто событие будет длиться в течение промежутка времени
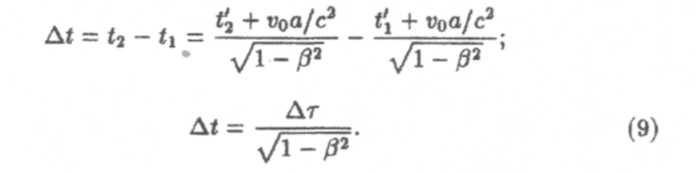
Из (9) вытекает, что длительность события, происходящего в некоторой точке, наименьшая в системе отсчета, относительно которой эта точка покоится. Собственное время∆τ, отсчитанное по часам, неподвижным относительно тела, всегда меньше, чем время ∆t, отсчитанное по часам, движущимся относительно тела. В пределе малых скоростей (v « с) длительности событий ∆t ≈∆τ.
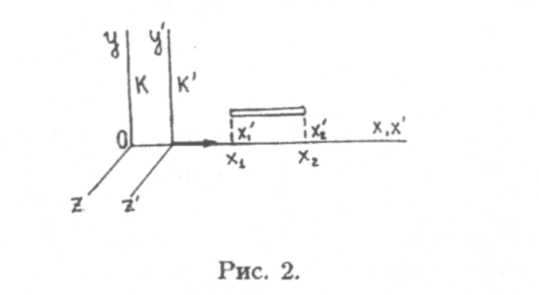
3. Относительность длины(размеров) тел. Рассмотрим стержень, расположенный вдоль оси х'и покоящийся относительно системы К'.Клина его в системе К'равна l0 = х'2 - х'1 (рис. 2).
В системе Кскорость стержня v0, координаты концов х1и х2надо отметить в один и тот же момент времени t1 = t2=t Длина стержня в системе Кравна l= х2 — х1.Чтобы найти связь между lи l0, используем преобразования (8):
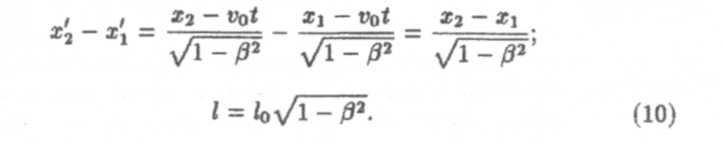
Линейные размеры тела наибольшие в той инерциальной системе отсчета, относительно которой тело покоится (l0 > l).При этом поперечные размеры тел одинаковы во всех инерциальных системах отсчета.
4. Релятивистский закон сложения скоростей.Скорости материальной точки вдоль оси х(рис, 1, 2) в системах Ки К'определяются как vx = dx/dtи v'x — dx'/dt'.Согласно преобразованиям Лоренца (8)
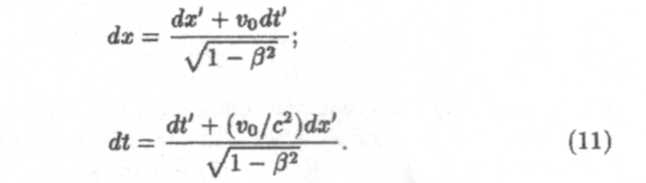
Разделив в (11) первое равенство на второе, получим релятивистский закон сложения скоростей:

Пусть скорость v'x = с. Тогда
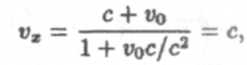
что является следствием постулата о постоянстве скорости света во всех системах отсчета. В приближении малых скоростей v« с имеем vx= v'x = v0, т.е. классический закон сложения скоростей (2).
Основной закон релятивистской динамики для материальной точки
В конце 19 века на опытах с быстро движущимися электронами было установлено, что масса тела зависит от его скорости, возрастая с увеличением скорости по закону

где mo — масса покоя, измеренная в неподвижной относительно тела системе отсчета, am — релятивистская масса, измеренная в системе отсчета, движущейся со скоростью v. При v < с т = mo = const. Основной закон динамики в релятивистской механике имеет вид:
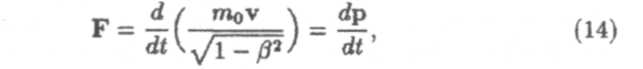
где р — релятивистский импульс:

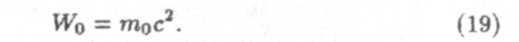
| Откуда следует, что покоящееся тело обладает энергиейпокоя |
Уравнения (14) и (15) внешне совпадают с основным уравнением классической механики, если в качестве массы брать релятивистскую массу т (13), но (14-15) инвариантны по отношению к преобразованию Лоренца (8). Взамкнутой системе релятивистский импульс системы сохраняется (р= const).
Дата добавления: 2015-08-11; просмотров: 784;
