Экстремум функции двух переменных.
Точка M0(x0,y0) является точкой максимума (минимума) функции z = f(x,y), если найдется такая окрестность точки M0, что для всех точек M(x,y) из этой окрестности выполняется неравенство f(x,y)< f(x0,y0) или ( f(x,y)> f(x0,y0)).
Точки максимума и минимума называются точками экстремума.

Рис.1 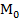 -точка максимума Рис.2
-точка максимума Рис.2 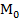 -точка минимума
-точка минимума
Сформулируем необходимые и достаточные условия существования экстремума:
Определение Точка 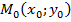 называется точкой минимума (максимума) функции z=f(x;y, если существует такая окрестность точки
называется точкой минимума (максимума) функции z=f(x;y, если существует такая окрестность точки 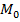 , что для всех точек M(x;y) из этой окрестности выполняется неравенство f
, что для всех точек M(x;y) из этой окрестности выполняется неравенство f 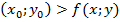 или f
или f 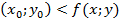 .
.
Точки минимума и максимума функции z= 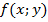 .называются точками экстремума, а значения функции в этих точках – экстремумами функции (минимумом и максимумом соответственно).
.называются точками экстремума, а значения функции в этих точках – экстремумами функции (минимумом и максимумом соответственно).
Заметим, что минимум и максимум функции имеют локальный характер, так как значение функции в точке 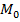 сравнивается с ее значениями в точках, достаточно близких к
сравнивается с ее значениями в точках, достаточно близких к 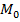 .
.
Теорема 1 (необходимые условия экстремума). Если 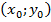 – точка экстремума дифференцируемой функции z=
– точка экстремума дифференцируемой функции z= 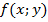 ., то ее частные производные
., то ее частные производные 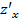 и
и 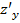 в этой точке равны нулю:
в этой точке равны нулю: 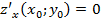 и
и 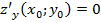
Точки, в которых частные производные первого порядка равны нулю, называются критическими или стационарными. В критических точках функция z= 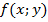 . может иметь экстремум, а может и не иметь.
. может иметь экстремум, а может и не иметь.
Теорема 2 (достаточное условие экстремума). Пусть функция z= 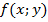 .: а) определена в некоторой окрестности критической точки
.: а) определена в некоторой окрестности критической точки 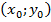 , в которой
, в которой 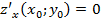 и
и 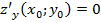
; б) имеет непрерывные частные производные второго порядка 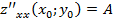
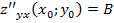
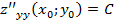 . Тогда, если
. Тогда, если 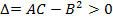 , то функция z=
, то функция z= 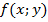 .: в точке
.: в точке 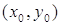 имеет экстремум: максимум, если А<0; минимум, если А>0; если
имеет экстремум: максимум, если А<0; минимум, если А>0; если 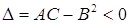 , то функция z=
, то функция z= 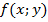 .: в точке
.: в точке 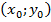 экстремума не имеет. В случае
экстремума не имеет. В случае 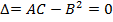 вопрос о наличии экстремума остается открытым.
вопрос о наличии экстремума остается открытым.
При исследовании функции двух переменных на экстремум рекомендуется использовать следующую схему:
1. Найти частные производные первого порядка: 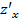 и
и 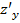 .
.
2. Решить систему уравнений 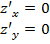 и найти критические точки функции.
и найти критические точки функции.
3. Найти частные производные второго порядка: 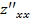 ,
, 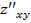 ,
, 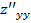 .
.
4. Вычислить значения частных производных второго порядка в каждой критической точке и, используя достаточные условия, сделать вывод о наличии экстремума.
5. Найти экстремумы функции.
Пример 1. Найти экстремумы функции z= 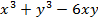 .
.
Решение. 1. Находим частные производные 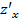 и
и 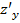 :
:
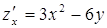 ,
, 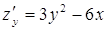 .
.
2. Для определения критических точек решаем систему уравнений
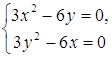
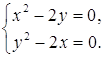
Из первого уравнения системы находим: y= 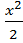 . Подставляя найденное значение y во второе уравнение, получим
. Подставляя найденное значение y во второе уравнение, получим 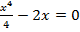 или , x(
или , x( 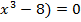 ,
,
Откуда 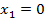 .
. 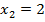
Находим значения y, соответствующие значениям 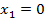 .
. 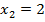
. Подставляя значения 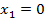 .
. 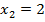 в уравнение
в уравнение 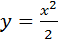 , получим:
, получим: 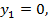 .
. 
Таким образом, имеем две критические точки: 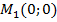 и
и 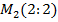 .
.
3. Находим частные производные второго порядка:
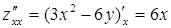 ;
; 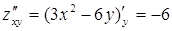 ;
; 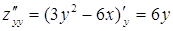 .
.
4. Вычисляем значения частных производных второго порядка в каждой критической точке. Для точки 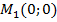 имеем:
имеем:
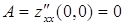 ,
, 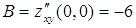 ,
, 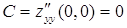 .
.
Так как
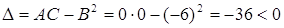 ,
,
то в точке 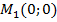 экстремума нет.
экстремума нет.
В точке 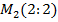 .:
.:
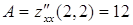 ,
, 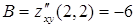 ,
, 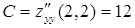
и, следовательно,
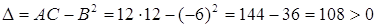 .
.
Значит, в силу достаточного условия экстремума, в точке 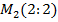 . функция имеет минимум, так как в этой точке
. функция имеет минимум, так как в этой точке 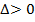 и A>0.
и A>0.
5. Находим значение функции в точке 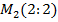 .:
.:
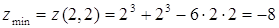 .
.
6. Условный экстремум
В теории функций нескольких переменных иногда возникают задачи, когда экстремум функции нескольких переменных необходимо найти не на всей области определения, а на множестве, удовлетворяющем некоторому условию.
Пусть z=f(x;y) – функция двух переменных, аргументы x и y которой удовлетворяют условию g(x;y)=C, называемому уравнением связи.
Определение 8. Точка 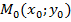 называется точкой условного минимума (максимума) функции z=f(x;y), если существует такая окрестность точки
называется точкой условного минимума (максимума) функции z=f(x;y), если существует такая окрестность точки 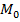 , что для всех точек M(x;y) из этой окрестности, удовлетворяющих условию g(x;y), выполняется неравенство f(
, что для всех точек M(x;y) из этой окрестности, удовлетворяющих условию g(x;y), выполняется неравенство f( 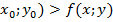 , (f(
, (f( 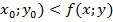 )
)
Если уравнение связи g(x;y)=C можно разрешить относительно одной из переменных (например, выразить y через x: y= 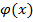 , то задача отыскания условного экстремума функции двух переменных сводится к нахождению экстремума функции одной переменной. Для этого подставляют найденное значение y=
, то задача отыскания условного экстремума функции двух переменных сводится к нахождению экстремума функции одной переменной. Для этого подставляют найденное значение y= 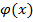 , в функцию двух переменных. В результате получают функцию одной переменной x: z=f(x,
, в функцию двух переменных. В результате получают функцию одной переменной x: z=f(x, 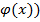 . Ее экстремум и будет условным экстремумом функции z=f(x;y).
. Ее экстремум и будет условным экстремумом функции z=f(x;y).
Пример 7. Найти экстремумы функции z=3 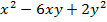 -7 при условии, что ее аргументы удовлетворяют уравнению связи y-3x= -1.
-7 при условии, что ее аргументы удовлетворяют уравнению связи y-3x= -1.
Решение. Из уравнения связи находим функцию y=3x-1 и подставляем ее в функцию z. Получим функцию одной переменной
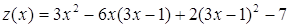
или z(x)=3 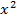 - 6x-5
- 6x-5
Находим экстремум данной функции:
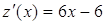
6x - 6= 0, x=1 - критическая точка первого рода (точка, подозрительная на экстремум). Так как 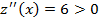 то в точке x=1 функция z(x) имеет локальный минимум. Из уравнения связи находим: y=3
то в точке x=1 функция z(x) имеет локальный минимум. Из уравнения связи находим: y=3 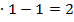 . Следовательно, функция
. Следовательно, функция
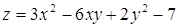
в точке M91;2) имеет условный минимум:
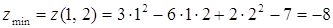 .
.
Дата добавления: 2015-08-11; просмотров: 1430;
