Метод наименьших квадратов. Пусть проводится n однородных испытаний или экспериментов, и результатом каждого испытания является пара чисел – значений некоторых переменных x и y

Пусть проводится n однородных испытаний или экспериментов, и результатом каждого испытания является пара чисел – значений некоторых переменных x и y. Испытание с номером i приводит к числам x_i, y_i. В качестве испытания можно, например, рассматривать выбор определенного предприятия в данной отрасли промышленности, величиной x считать объем производства продукции (например в миллионах рублей), величиной y – объем экспорта этого вида продукции (в миллионах рублей), и обследовать n предприятий отрасли.

Итогом этих испытаний является таблица:

			. . .
			. . .

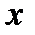
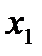
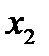
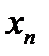
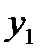
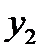
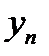
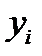где каждому числу x_i (величину рассматриваем как независимый показатель или фактор) поставлено в соответствие число (величину 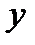рассматриваем как зависимый показатель – результат).

В качестве значений часто рассматриваются моменты времени: t₁, t₂, ..., t_n, взятые через равные промежутки. Тогда таблица

			. . .
			. . .

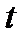
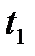
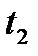
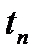
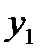
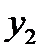
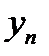
называется временным рядом.

Нас интересует вопрос, как найти приближенную формулу для функции y = f(x), которая “наилучшим образом” описывала бы данные таблицы.

Пусть точки с координатами (x_i,y_i) группируются на плоскости вдоль некоторой прямой. Задача заключается в том, чтобы найти параметры a₀ и a₁ этой прямой:

y = a₀ + a₁x, (1)

причем это нужно сделать так, чтобы она лучше любой другой прямой соответствовала расположению на плоскости экспериментальных точек (x_i, y_i).

Признаком наилучшей прямой считается минимум суммы квадратов отклонений фактических значений y, полученных из таблицы, от вычисленных по формуле (1). Эта сумма квадратов рассчитывается по формуле

S² = (y₁ – (a₀ + a₁x₁))² + (y₂ – (a₀ + a₁x₂))² +...+ (y_n – (a₀ + a₁x_n))² =

.

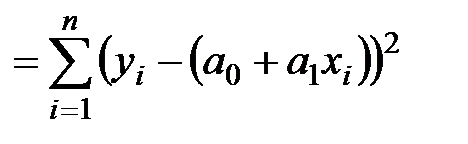Обратим внимание на то, что все x_i и y_i — известные из таблицы числа, а S² есть функция двух переменных a₀ и a₁.

S² = S²(a₀,a₁)

Можно показать, что график функции S² выглядит примерно так, как изображено на рисунке. Единственная точка, в которой обе частные производ­ные 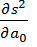и 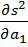равны нулю, является точкой минимума.

Отсюда следует, что точку минимума можно искать, используя лишь необходимые условия экстремума:

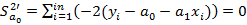(2)

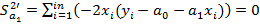. (3)

На самом деле для функции S² = S²(a₀,a₁) достаточно легко проверить выполнение достаточных условия экстремума. тогда Уравнения (2) и (3) можно преобразовать:

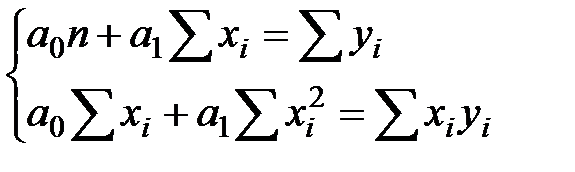. (4)

Получилась так называемая система нормальных уравнений относительно неизвестных величин a₀ и a₁.

Формула (1) с параметрами a₀, a₁ определенными из системы (4), называется уравнением регрессии. Прямая линия, описываемая этим уравнением, называется линией регрессии. Для временных рядов обычно вместо слова “регрессия” употребляется слово тренд.

Если экспериментальные точки в плоскости XOY группируются вдоль некоторой кривой линии, то можно подобрать вместо формулы (1) другую подходящую формулу, например, y = a₀ + a₁x + a₂x² или y = a₀ exp(a₁x) с параметрами соответственно a₀, a₁, a₂ и a₀, a₁, подставить ее в выражение 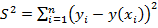и искать минимум получившейся функции S² при помощи частных производных по параметрам.