Геометрическая интерпретация частных производных функции двух переменных

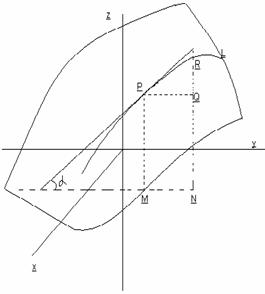
Пусть уравнение z=f(x,y) –это уравнение поверхности. Проведем плоскость x=const. L- линия пересечения поверхности с плоскостью x=const. При данном x на плоскости ХОУ возьмем точку М. На поверхности z=f(x,y) ей соответствует точка Р(x,y,z). Дадим переменному y приращение 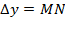Тогда функция z получит приращение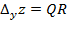

Отношение 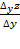равно тангенсу угла, образованного секущей RР с положительным направлением оси ОУ,

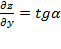
Итак, частная производная 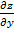численно равна тангенсу угла

наклона касательной к кривой, получающейся в сечении поверхности z=f(x,y) плоскостью x=const.

Аналогично, частная производная 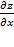численно равна тангенсу угла наклона касательной к кривой, получающейся в сечении поверхности z=f(x,y) плоскостью x=const.