Астные производные.

Пусть z=f(x,y). Зафиксируем какую-либо точку (x,y), а затем, не меняя закрепленного значения аргумента y, придадим аргументу x приращение 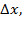Тогда z получит приращение, которое называется частным приращением z по x и обозначается 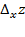и определяется формулой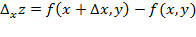

Аналогично, если x сохраняет постоянное значение, а y получает приращение 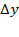, то z получает частное приращение z по y,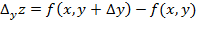

Определение. Частной производной по x от функции z=f(x,y) называется предел отношения частного приращения 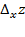по x к приращению 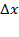при стремлении 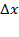к нулю, т.е.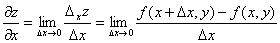

Частная производная обозначается одним из символов.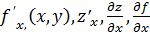

Аналогично определяется частная производная по y:

.

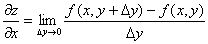Таким образом, частные производные функции двух переменных вычисляются по тем же правилам, что и производные функции одного переменного.

Пример.

1. Найти частные производные функции z=x²e ^x-2y.

Решение.

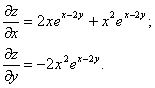
2. Z= 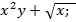. Решение: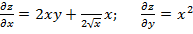

3. Z= 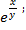Решение: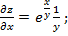

.

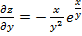
Частные производные функции любого числа переменных определяются аналогично.