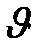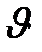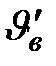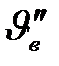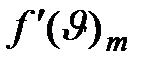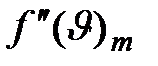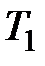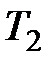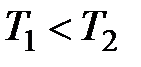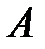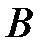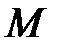Распределение молекул газа по скоростям
(распределение Максвелла)
Беспорядочность движения молекул в условиях термодинамического равновесия газа приходит к наличию определенных закономерностей. Одна из таких закономерностей состоит в распределении молекул по скоростям. Хаотичность движения молекул и столкновения между ними приводит к тому, что молекулы имеют различные скорости. Установить закон распределения молекул по скоростям означало, казалось бы, определить число молекул, обладающих той или иной заданной скоростью. Но именно в силу случайного, беспорядочного характера движения молекул (даже при очень большом числе их в рассматриваемом объеме газа) может не оказаться ни одной молекулы, обладающей определенной заданной скоростью. Поэтому задача сводится к определению числа молекул, обладающих скоростями, лежащими в некотором интервале от 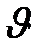 до
до 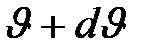 .
.
Для молекул идеального газа, находящегося в термодинамическом равновесии, эта задача впервые была решена Максвеллом. Он установил, что среди 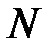 молекул, находящихся в единице объема, число
молекул, находящихся в единице объема, число  таких молекул, скорости которых лежат в интервале от
таких молекул, скорости которых лежат в интервале от 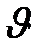 до
до 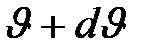 , оказывается равным
, оказывается равным

| (2.4)
|
Величина 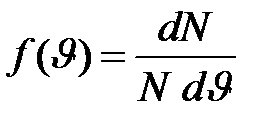 , численно равная доле молекул, скорости которых лежат в единичном интервале скоростей вблизи скорости
, численно равная доле молекул, скорости которых лежат в единичном интервале скоростей вблизи скорости 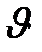 , называется функцией распределения. В соответствии с вышеприведенными формулами она будет иметь вид:
, называется функцией распределения. В соответствии с вышеприведенными формулами она будет иметь вид:
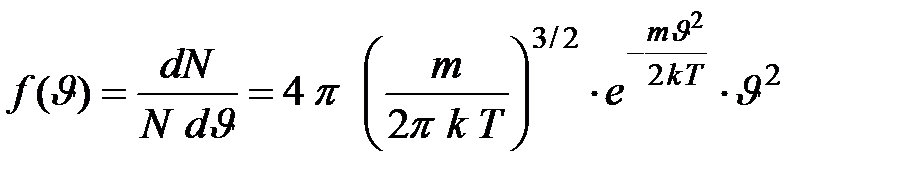
| (2.5)
|
График ее представлен на рис. 2.2. По графику можно определить долю молекул, обладающих скоростями, лежащими в интервале от 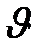 до
до 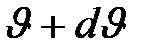 . Она будет равна площади заштрихованной полосы с основанием
. Она будет равна площади заштрихованной полосы с основанием 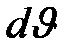 и высотой
и высотой  . Вся площадь, ограниченная кривой распределения, равна единице. Это условие записывается следующим образом:
. Вся площадь, ограниченная кривой распределения, равна единице. Это условие записывается следующим образом:
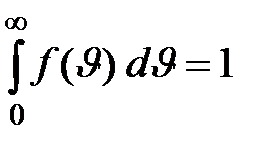
|
| Из графика видно, что при  и и 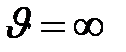 функция распределения обращается в нуль. Это означает, что неподвижных молекул, а также молекул, имеющих очень большие скорости, в газе нет. Существует такая скорость функция распределения обращается в нуль. Это означает, что неподвижных молекул, а также молекул, имеющих очень большие скорости, в газе нет. Существует такая скорость 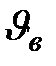 , которой обладает максимальное количество молекул газа.
Эта скорость соответствует максимуму кривой распределения и называется наиболее вероятной скоростью. , которой обладает максимальное количество молекул газа.
Эта скорость соответствует максимуму кривой распределения и называется наиболее вероятной скоростью.
|
Для нахождения ее значения необходимо определить максимум функции (2.5). Для этого возьмем первую производную  по
по 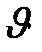 и приравняем ее к нулю:
и приравняем ее к нулю:
или
Полученное равенство справедливо при условии  , из которого следует, что наиболее вероятная скорость
, из которого следует, что наиболее вероятная скорость
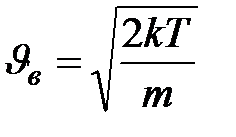
| (2.6)
|
Следует обратить внимание на то, что кривая распределения несимметрична: правая часть более пологая, чем левая. Это означает, что площадь, ограниченная правой частью кривой и осью абсцисс, больше, чем площадь, ограниченная левой частью кривой и осью абсцисс. А так как эти площади пропорциональны числу молекул, то число молекул, обладающих скоростями, большими, чем наиболее вероятная скорость, будет большим. Поэтому средняя арифметическая скорость не равна наиболее вероятной, а больше нее.
Найдем среднюю арифметическую скорость  теплового движения молекул. Выражение
теплового движения молекул. Выражение 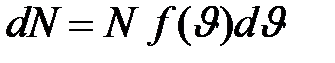 определяет число молекул, скорости которых лежат в бесконечно малом интервале от
определяет число молекул, скорости которых лежат в бесконечно малом интервале от 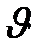 до
до  . Умножая
. Умножая 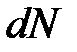 на
на 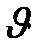 , получим сумму скоростей, лежащих в заданном бесконечно малом интервале. Интегрирование по скорости в пределах от 0 до
, получим сумму скоростей, лежащих в заданном бесконечно малом интервале. Интегрирование по скорости в пределах от 0 до 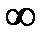 даст общую сумму всех скоростей молекул при данной температуре. Разделив эту сумму на полное число молекул в рассматриваемом объеме, получим среднюю арифметическую скорость. Итак,
даст общую сумму всех скоростей молекул при данной температуре. Разделив эту сумму на полное число молекул в рассматриваемом объеме, получим среднюю арифметическую скорость. Итак,
Выразив значение  из формулы (2.5), получим:
из формулы (2.5), получим:
Решение интеграла дает:
Окончательно получим:

| (2.7)
|
Итак, согласно формулам (1.28а), (2.6) и (2.7) существуют три скорости движения молекул в газе:
|
наиболее вероятная
средняя арифметическая
средняя квадратичная
| 

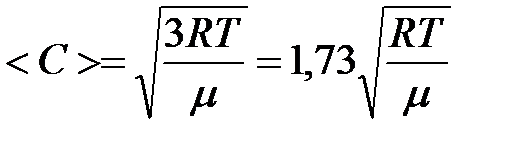
|
На распределение молекул по скоростям большое влияние оказывает температура. Так как 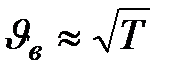 , то с повышением температуры максимум кривой распределения смещается вдоль оси абсцисс вправо. А, поскольку площадь, ограниченная кривой, не должна изменяться, то, очевидно, что величина ординаты, соответствующая максимуму, уменьшается. Кривая распределения становится более пологой (рис. 2.3).
, то с повышением температуры максимум кривой распределения смещается вдоль оси абсцисс вправо. А, поскольку площадь, ограниченная кривой, не должна изменяться, то, очевидно, что величина ординаты, соответствующая максимуму, уменьшается. Кривая распределения становится более пологой (рис. 2.3).
|
| Это означает, что число медленных молекул убывает, а число быстрых – возрастает.
Существуют различные методы определения скоростей молекул газа. Один из таких методов был впервые осуществлен в 1920 году Штерном. Прибор, предназначенный для этой цели, состоял из двух коаксиальных цилиндров  и и 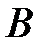 (рис. 2.4), по оси которых проходила, покрытая серебром, вольфрамовая нить. (рис. 2.4), по оси которых проходила, покрытая серебром, вольфрамовая нить.
|
При пропускании тока через вольфрамовую нить серебро испарялось. Его атомы летели к поверхности цилиндра  , на которой по всей длине была сделана узкая щель, параллельная вольфрамовой нить. Пройдя через щель, атомы серебра попадали на внутреннюю поверхность цилиндра
, на которой по всей длине была сделана узкая щель, параллельная вольфрамовой нить. Пройдя через щель, атомы серебра попадали на внутреннюю поверхность цилиндра 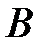 . При неподвижных цилиндрах пучок атомов серебра «оседал» на внутренней поверхности цилиндра
. При неподвижных цилиндрах пучок атомов серебра «оседал» на внутренней поверхности цилиндра 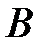 строго напротив щели и давал ее изображение в точке
строго напротив щели и давал ее изображение в точке 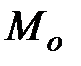 . Если прибор привести во вращение с угловой скоростью
. Если прибор привести во вращение с угловой скоростью 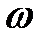 , то серебряный налет окажется не напротив щели, а сместится на некоторое расстояние
, то серебряный налет окажется не напротив щели, а сместится на некоторое расстояние 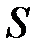 в точку
в точку 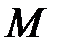 . Такое смещение возникнет в результате того, что за время
. Такое смещение возникнет в результате того, что за время 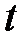 полета атома от щели до внутренней поверхности цилиндра
полета атома от щели до внутренней поверхности цилиндра  , последний повернется на угол
, последний повернется на угол 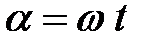 .
.
|
| Если радиус цилиндра  обозначить через обозначить через 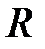 , а радиус цилиндра , а радиус цилиндра 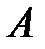 - через - через 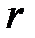 , то время полета атома от щели до поверхности цилиндра , то время полета атома от щели до поверхности цилиндра 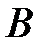 будет равно: будет равно:
 (2.8)
где (2.8)
где 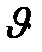 - скорость атома. - скорость атома.
|
За время 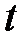 точка
точка 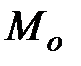 на стенке цилиндра
на стенке цилиндра 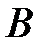 «пройдет» путь
«пройдет» путь  , который равен
, который равен
Если за 1 с прибор делает  оборотов, то
оборотов, то
Подставив выражение (2.8), получим

| (2.9)
|
Из формулы (2.9) видно, что, если скорости движения атомов серебра различны, то на внутренней стенке цилиндра  они будут осаждаться на различных расстояниях от точки
они будут осаждаться на различных расстояниях от точки 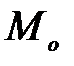 : атомы с большими скоростями – ближе к точке
: атомы с большими скоростями – ближе к точке  , атомы с меньшими скоростями – дальше от точки
, атомы с меньшими скоростями – дальше от точки  . В том месте, где осядет большее количество атомов, толщина серебряного налета будет больше. На рис. 2.5 изображено сечение налета серебра на внутренней стенке цилиндра
. В том месте, где осядет большее количество атомов, толщина серебряного налета будет больше. На рис. 2.5 изображено сечение налета серебра на внутренней стенке цилиндра 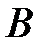 . Если бы все атомы серебра двигались с одинаковой скоростью, то серебряный налет смещался бы, не изменяя своей формы.
. Если бы все атомы серебра двигались с одинаковой скоростью, то серебряный налет смещался бы, не изменяя своей формы.
|
| На опыте наблюдалось не только смещение налета, но и «размытость» его границ. Это подтверждает то, что атомы серебра имеют различные скорости, причем относительное большинство атомов осаждается вблизи точки 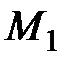 , соответствующей максимальной толщине серебряного налета. , соответствующей максимальной толщине серебряного налета.
|
Результаты опыта показали, что этим атомам в максвелловском распределении молекул по скоростям соответствует наиболее вероятная скорость. Изменение толщины налета серебра в различных местах полоски позволяет судить о характере распределения атомов по скоростям.
Дата добавления: 2015-08-11; просмотров: 1202;
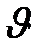 до
до 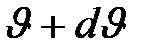 .
.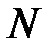 молекул, находящихся в единице объема, число
молекул, находящихся в единице объема, число  таких молекул, скорости которых лежат в интервале от
таких молекул, скорости которых лежат в интервале от 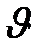 до
до 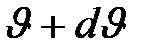 , оказывается равным
, оказывается равным
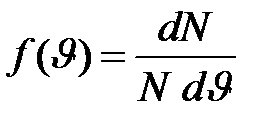 , численно равная доле молекул, скорости которых лежат в единичном интервале скоростей вблизи скорости
, численно равная доле молекул, скорости которых лежат в единичном интервале скоростей вблизи скорости 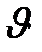 , называется функцией распределения. В соответствии с вышеприведенными формулами она будет иметь вид:
, называется функцией распределения. В соответствии с вышеприведенными формулами она будет иметь вид: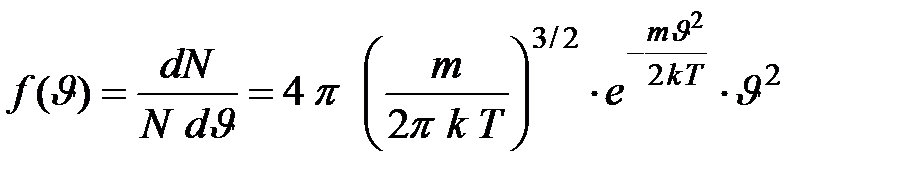
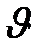 до
до 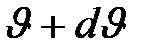 . Она будет равна площади заштрихованной полосы с основанием
. Она будет равна площади заштрихованной полосы с основанием 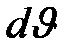 и высотой
и высотой  . Вся площадь, ограниченная кривой распределения, равна единице. Это условие записывается следующим образом:
. Вся площадь, ограниченная кривой распределения, равна единице. Это условие записывается следующим образом: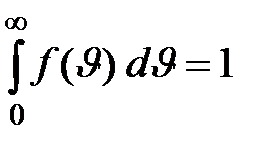
 и
и 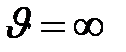 функция распределения обращается в нуль. Это означает, что неподвижных молекул, а также молекул, имеющих очень большие скорости, в газе нет. Существует такая скорость
функция распределения обращается в нуль. Это означает, что неподвижных молекул, а также молекул, имеющих очень большие скорости, в газе нет. Существует такая скорость 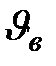 , которой обладает максимальное количество молекул газа.
Эта скорость соответствует максимуму кривой распределения и называется наиболее вероятной скоростью.
, которой обладает максимальное количество молекул газа.
Эта скорость соответствует максимуму кривой распределения и называется наиболее вероятной скоростью.
 по
по 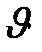 и приравняем ее к нулю:
и приравняем ее к нулю: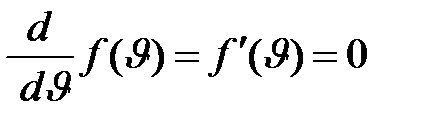
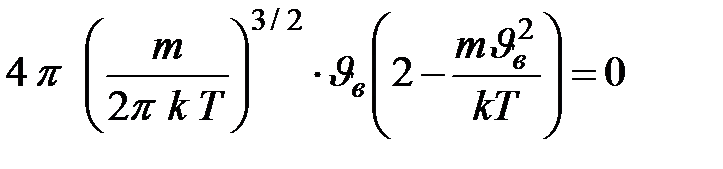
 , из которого следует, что наиболее вероятная скорость
, из которого следует, что наиболее вероятная скорость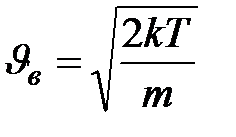
 теплового движения молекул. Выражение
теплового движения молекул. Выражение 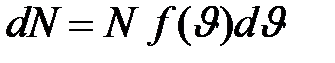 определяет число молекул, скорости которых лежат в бесконечно малом интервале от
определяет число молекул, скорости которых лежат в бесконечно малом интервале от 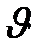 до
до  . Умножая
. Умножая 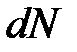 на
на 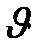 , получим сумму скоростей, лежащих в заданном бесконечно малом интервале. Интегрирование по скорости в пределах от 0 до
, получим сумму скоростей, лежащих в заданном бесконечно малом интервале. Интегрирование по скорости в пределах от 0 до 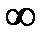 даст общую сумму всех скоростей молекул при данной температуре. Разделив эту сумму на полное число молекул в рассматриваемом объеме, получим среднюю арифметическую скорость. Итак,
даст общую сумму всех скоростей молекул при данной температуре. Разделив эту сумму на полное число молекул в рассматриваемом объеме, получим среднюю арифметическую скорость. Итак,
 из формулы (2.5), получим:
из формулы (2.5), получим: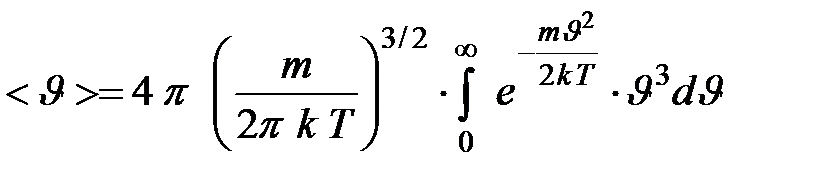
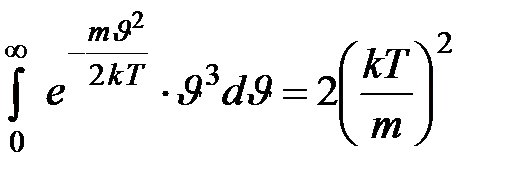



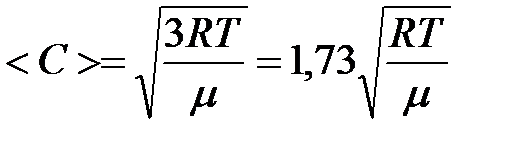
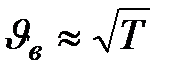 , то с повышением температуры максимум кривой распределения смещается вдоль оси абсцисс вправо. А, поскольку площадь, ограниченная кривой, не должна изменяться, то, очевидно, что величина ординаты, соответствующая максимуму, уменьшается. Кривая распределения становится более пологой (рис. 2.3).
, то с повышением температуры максимум кривой распределения смещается вдоль оси абсцисс вправо. А, поскольку площадь, ограниченная кривой, не должна изменяться, то, очевидно, что величина ординаты, соответствующая максимуму, уменьшается. Кривая распределения становится более пологой (рис. 2.3). и
и 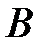 (рис. 2.4), по оси которых проходила, покрытая серебром, вольфрамовая нить.
(рис. 2.4), по оси которых проходила, покрытая серебром, вольфрамовая нить.
 , на которой по всей длине была сделана узкая щель, параллельная вольфрамовой нить. Пройдя через щель, атомы серебра попадали на внутреннюю поверхность цилиндра
, на которой по всей длине была сделана узкая щель, параллельная вольфрамовой нить. Пройдя через щель, атомы серебра попадали на внутреннюю поверхность цилиндра 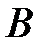 . При неподвижных цилиндрах пучок атомов серебра «оседал» на внутренней поверхности цилиндра
. При неподвижных цилиндрах пучок атомов серебра «оседал» на внутренней поверхности цилиндра 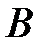 строго напротив щели и давал ее изображение в точке
строго напротив щели и давал ее изображение в точке 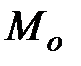 . Если прибор привести во вращение с угловой скоростью
. Если прибор привести во вращение с угловой скоростью 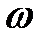 , то серебряный налет окажется не напротив щели, а сместится на некоторое расстояние
, то серебряный налет окажется не напротив щели, а сместится на некоторое расстояние 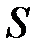 в точку
в точку 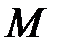 . Такое смещение возникнет в результате того, что за время
. Такое смещение возникнет в результате того, что за время 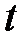 полета атома от щели до внутренней поверхности цилиндра
полета атома от щели до внутренней поверхности цилиндра  , последний повернется на угол
, последний повернется на угол 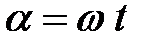 .
. обозначить через
обозначить через 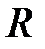 , а радиус цилиндра
, а радиус цилиндра 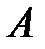 - через
- через 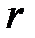 , то время полета атома от щели до поверхности цилиндра
, то время полета атома от щели до поверхности цилиндра 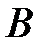 будет равно:
будет равно:
 (2.8)
где
(2.8)
где 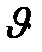 - скорость атома.
- скорость атома.
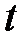 точка
точка 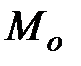 на стенке цилиндра
на стенке цилиндра 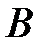 «пройдет» путь
«пройдет» путь  , который равен
, который равен
 оборотов, то
оборотов, то

 они будут осаждаться на различных расстояниях от точки
они будут осаждаться на различных расстояниях от точки 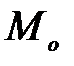 : атомы с большими скоростями – ближе к точке
: атомы с большими скоростями – ближе к точке  , атомы с меньшими скоростями – дальше от точки
, атомы с меньшими скоростями – дальше от точки  . В том месте, где осядет большее количество атомов, толщина серебряного налета будет больше. На рис. 2.5 изображено сечение налета серебра на внутренней стенке цилиндра
. В том месте, где осядет большее количество атомов, толщина серебряного налета будет больше. На рис. 2.5 изображено сечение налета серебра на внутренней стенке цилиндра 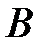 . Если бы все атомы серебра двигались с одинаковой скоростью, то серебряный налет смещался бы, не изменяя своей формы.
. Если бы все атомы серебра двигались с одинаковой скоростью, то серебряный налет смещался бы, не изменяя своей формы.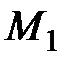 , соответствующей максимальной толщине серебряного налета.
, соответствующей максимальной толщине серебряного налета.