Следовательно, для всей системы в целом справедливо равенство

dWк + dWп = 0,

откуда полная механическая энергия замкнутой системы

W^к + W^п = const. (3.3)

Выражение (3.3) представляет собойзакон сохранения механической энергии:в замкнутой системе тел, между которыми действуют только консервативные силы, механическая энергия сохраняется, т. е. не изменяется со временем.

Будем рассматривать только замкнутые консервативные системы, т. е. систе­мы, в которых взаимные превращения механической энергии в другие виды от­сутствуют. Тогда справедлив закон сохранения энергии в форме (3.3). Рассмотрим графическое представление потенциальной энергии для тела в однородном поле тяжести и для упругодеформированного тела.

Потенциальная энергия тела массой т, поднятого на высоту h над поверхно­стью земли: W_п = mgh. График данной зависимости W_п = f(h) - прямая линия, проходящая через начало координат (рис.3.1), угол наклона кото­рой к оси h тем больше, чем больше масса тела (так как tg 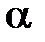= mg).

Если полная энергия тела равна Е (прямая, параллельная оси h), то оно на высоте h обладает потенциальной энергией W_п , которая определяется отрезком вертикали, заключенным между точкой h на оси абсцисс и графиком W_п. Естественно, что кинетическая энергия W_к задается отрезком вертикали между графиком W_п и горизонтальной прямой ЕЕ. Из рис.3.1 следует, что при h = h_max, W_к = 0 и W_п = E = mgh, т. е. потенциальная энергия становится максимальной и равной полной энергии.

Из приведенного графика можно найти скорость тела на высоте h:

W_к = Е – W_п ,

т. е.

,

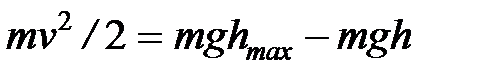откуда

.

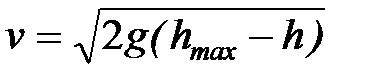Зависимость потенциальной энергии W_п упругодеформированного тела от величины деформации х определяется выражением W = kx² /2 и имеет вид параболы (рис.3.2), где заданная полная энергия тела E определяется горизонтальной прямой, параллельной оси абсцисс, а значения W_к и W_п задаются так же, как на рис.3.1.

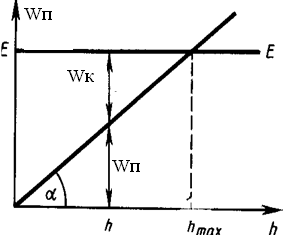Рис.3.1

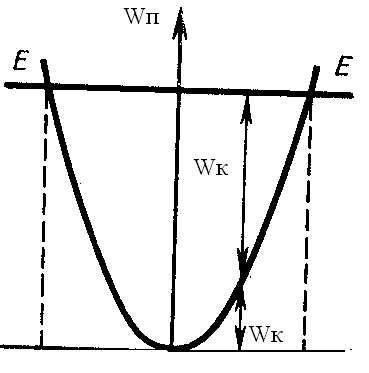Рис.3.2

С возрастанием деформации х потенциаль­ная энергия тела возрастает, а кинетическая - уменьшается. Абсцисса х_max определяет максимально возможную деформацию растяжения тела, а (-x_max) - максимально возможную деформацию сжатия тела. При х = ± x_max W_к = 0 и W_п = E = kx 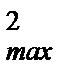/2, т. е. потенциальная энергия становится максимальной и равной полной энергии.

Скорость v упругодеформированного тела можно определить, как и в предыдущем случае:

W_к = Е - W_п ,

mv²/ 2 = kx 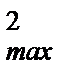/ 2 – kx²/ 2,

При полной энергии тела, равной Е, тело не может сместиться правее x_max и левее (-x_max), так как кинетическая энергия не может быть отрицательной величиной и, следовательно, потенциальная энергия не может быть больше полной. В таком случае говорят, что тело находится в потенциальной яме с координатами (-x_max)< х < x_max.