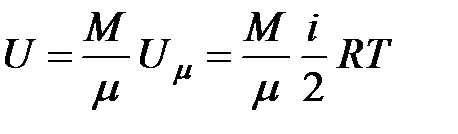Число степеней свободы – это число независимых координат, с помощью которых определяется положение тела в пространстве.
Молекула одноатомного газа, подобно материальной точке (рис. 2.1, а) имеет три степени свободы поступательного движения 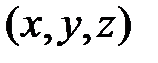 . Молекулу двухатомного газа (рис.2.1, б) можно представить в виде системы двух атомов, отстоящих друг от друга на некотором расстоянии и жестко связанных между собой. Такая молекула имеет пять степеней свободы, три из которых характеризуют поступательное движение молекулы в целом, а две – вращательное движение вокруг осей
. Молекулу двухатомного газа (рис.2.1, б) можно представить в виде системы двух атомов, отстоящих друг от друга на некотором расстоянии и жестко связанных между собой. Такая молекула имеет пять степеней свободы, три из которых характеризуют поступательное движение молекулы в целом, а две – вращательное движение вокруг осей  и
и 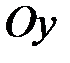 .
.
Вращением вокруг оси 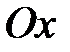 можно пренебречь, так как момент инерции атомов относительно этой оси, а следовательно, и кинетическая энергия, связанные с этим вращением, ничтожно малы. Трехатомная молекула с нелинейным расположением атомов (рис.2.1, с) имеет шесть степеней свободы - три степени свободы поступательного движения молекулы и три степени свободы вращательного.
можно пренебречь, так как момент инерции атомов относительно этой оси, а следовательно, и кинетическая энергия, связанные с этим вращением, ничтожно малы. Трехатомная молекула с нелинейным расположением атомов (рис.2.1, с) имеет шесть степеней свободы - три степени свободы поступательного движения молекулы и три степени свободы вращательного.
Степени свободы, связанные с колебательным движением, в обычных условиях можно не учитывать, так как у большинства молекул колебания возбуждаются при высоких температурах порядка 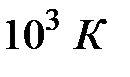 .
.
В силу хаотичности молекулярного движения ни одна из степеней свободы поступательного движения, так же, как ни одна степень свободы вращательного движения, не имеет преимущества перед другими. Так как средняя кинетическая энергия поступательного движения одноатомной молекулы равна 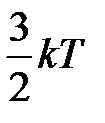 , то эта энергия приходится на три степени свободы поступательного движения молекулы, тогда на одну степень свободы приходится
, то эта энергия приходится на три степени свободы поступательного движения молекулы, тогда на одну степень свободы приходится 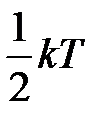 . Ни один из видов движения не имеет преимущества перед другим и виды движения могут переходить один в другой. Поэтому в условиях теплового равновесия газа на каждую степень свободы поступательного и вращательного движения, в среднем, приходится одинаковая кинетическая энергия, равная
. Ни один из видов движения не имеет преимущества перед другим и виды движения могут переходить один в другой. Поэтому в условиях теплового равновесия газа на каждую степень свободы поступательного и вращательного движения, в среднем, приходится одинаковая кинетическая энергия, равная 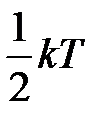 . В этом и заключается закон равного распределения энергии по степеням свободы.
. В этом и заключается закон равного распределения энергии по степеням свободы.
Если молекула имеет 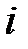 степеней свободы, то ее средняя кинетическая энергия будет равна
степеней свободы, то ее средняя кинетическая энергия будет равна
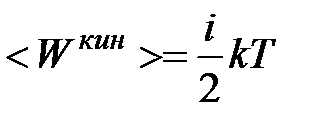
| (2.1)
|
Внутренняя энергия идеального газа представляет собой суммарную кинетическую энергию теплового движения всех молекул. Внутренняя энергия одного киломоля идеального газа равна сумме средних кинетических энергий  молекул:
молекул:
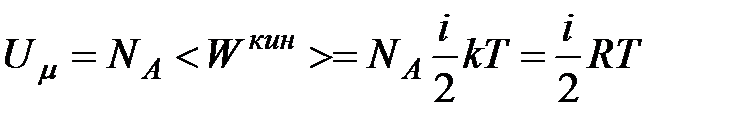
| (2.2)
|
Для некоторой массы газа, содержащей 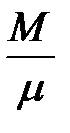 киломолей, внутренняя энергия равна
киломолей, внутренняя энергия равна
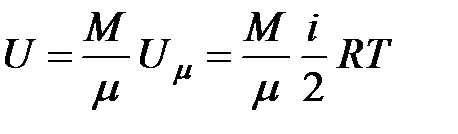
| (2.3)
|
Из приведенных формул видно, что внутренняя энергия газа зависит от количества газа, его температуры, числа атомов, образующих молекулу, т.е. зависит от природы газа.
Дата добавления: 2015-08-11; просмотров: 810;
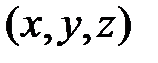 . Молекулу двухатомного газа (рис.2.1, б) можно представить в виде системы двух атомов, отстоящих друг от друга на некотором расстоянии и жестко связанных между собой. Такая молекула имеет пять степеней свободы, три из которых характеризуют поступательное движение молекулы в целом, а две – вращательное движение вокруг осей
. Молекулу двухатомного газа (рис.2.1, б) можно представить в виде системы двух атомов, отстоящих друг от друга на некотором расстоянии и жестко связанных между собой. Такая молекула имеет пять степеней свободы, три из которых характеризуют поступательное движение молекулы в целом, а две – вращательное движение вокруг осей  и
и 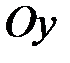 .
.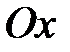 можно пренебречь, так как момент инерции атомов относительно этой оси, а следовательно, и кинетическая энергия, связанные с этим вращением, ничтожно малы. Трехатомная молекула с нелинейным расположением атомов (рис.2.1, с) имеет шесть степеней свободы - три степени свободы поступательного движения молекулы и три степени свободы вращательного.
можно пренебречь, так как момент инерции атомов относительно этой оси, а следовательно, и кинетическая энергия, связанные с этим вращением, ничтожно малы. Трехатомная молекула с нелинейным расположением атомов (рис.2.1, с) имеет шесть степеней свободы - три степени свободы поступательного движения молекулы и три степени свободы вращательного.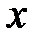
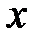
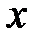
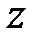
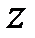
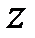
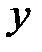
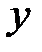
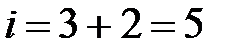

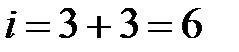
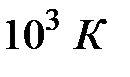 .
.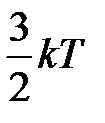 , то эта энергия приходится на три степени свободы поступательного движения молекулы, тогда на одну степень свободы приходится
, то эта энергия приходится на три степени свободы поступательного движения молекулы, тогда на одну степень свободы приходится 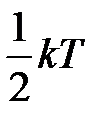 . Ни один из видов движения не имеет преимущества перед другим и виды движения могут переходить один в другой. Поэтому в условиях теплового равновесия газа на каждую степень свободы поступательного и вращательного движения, в среднем, приходится одинаковая кинетическая энергия, равная
. Ни один из видов движения не имеет преимущества перед другим и виды движения могут переходить один в другой. Поэтому в условиях теплового равновесия газа на каждую степень свободы поступательного и вращательного движения, в среднем, приходится одинаковая кинетическая энергия, равная 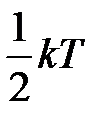 . В этом и заключается закон равного распределения энергии по степеням свободы.
. В этом и заключается закон равного распределения энергии по степеням свободы.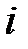 степеней свободы, то ее средняя кинетическая энергия будет равна
степеней свободы, то ее средняя кинетическая энергия будет равна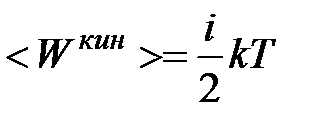
 молекул:
молекул: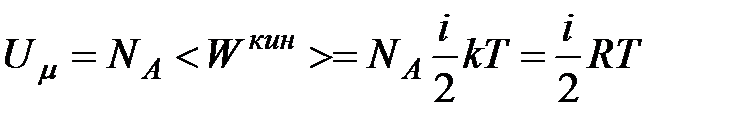
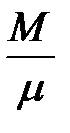 киломолей, внутренняя энергия равна
киломолей, внутренняя энергия равна