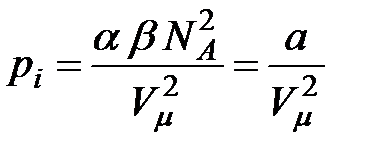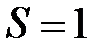Уравнение Ван-дер-Ваальса.
Рассмотренное в § 1 основное уравнение молекулярно-кинетической теории идеального газа, которое по существу является уравнением состояния этого газа, выведено в предположении, что молекулы газа не имеют собственных размеров и не взаимодействуют между собой (взаимодействие учитывалось только при столкновении молекул). Реальные газы подчиняются законам идеального газа лишь приближенно в том случае, когда давление газа мало и температура не слишком низкая. Поэтому при расчете работы тепловых машин и двигателей внутреннего сгорания с достаточной степенью точности можно использовать уравнение Менделеева-Клапейрона (1.2). Однако, в современной технике широко используются и высокие давления (при хранении и перевозке чистых газов, в паровых котлах, при выстреле в стволе орудия, при взрывах атомных и водородных бомб и т.д.). При больших давлениях и плотностях реальный газ отличается от идеального – здесь приходится учитывать силы взаимодействия и собственные размеры молекул.
Поскольку положительный и отрицательный заряд молекулы компенсируют друг друга, то электрическое поле за пределами молекулы очень быстро убывает с расстоянием. Практически его можно считать обращающимся в нуль уже на расстоянии двух-трех диаметров молекул. Поэтому на больших расстояниях силы взаимодействия между молекулами пренебрежимо малы (рис. 3.1 а). При сближении до расстояний порядка двух-трех диаметров постепенно начинают проявляться взаимодействия между ядрами молекул и их электронными оболочками. Благодаря притяжению разноименных и отталкиванию одноименных зарядов происходит некоторая деформация взаимодействующих молекул; между молекулами возникают силы притяжения (рис. 3.1 б). По мере дальнейшего сближения деформация молекул и силы притяжения будут возрастать, однако, когда молекулы подойдут «вплотную» друг к другу и соприкоснутся своими электронными оболочками, дальнейшее сближение окажется невозможным. Между молекулами возникают огромные силы отталкивания, резко возрастающие по мере дальнейшего взаимного проникновения оболочек (рис. 3.1 в).
|
| Абсолютная величина сил взаимодействия будет зависеть не только от расстояний, но и от строения взаимодействующих молекул и их взаимной ориентации. Однако общий характер зависимости  от от 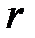 для любых молекул будет качественно одинаков: притяжение - на больших расстояниях и отталкивание – на малых. Важно заметить, что силы притяжения и отталкивания действуют одновременно, но в зависимости от расстояния между молекулами одна из них будет преобладающей. На расстоянии для любых молекул будет качественно одинаков: притяжение - на больших расстояниях и отталкивание – на малых. Важно заметить, что силы притяжения и отталкивания действуют одновременно, но в зависимости от расстояния между молекулами одна из них будет преобладающей. На расстоянии 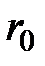 силы притяжения и отталкивания уравновешивают друг друга (рис. 3.2). силы притяжения и отталкивания уравновешивают друг друга (рис. 3.2).
|
Силам притяжения и отталкивания соответствуют свои значения потенциальной энергии. Суммарная кривая, дающая полную взаимную потенциальную энергию двух молекул, представлена на рис. 3.3.
Ветвь  соответствуют тому, что на малых расстояниях суммарная сила является силой отталкивания; ветвь
соответствуют тому, что на малых расстояниях суммарная сила является силой отталкивания; ветвь 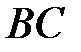 соответствует тому, что суммарная сила взаимодействия между молекулами на больших расстояниях является силой притяжения. Точка
соответствует тому, что суммарная сила взаимодействия между молекулами на больших расстояниях является силой притяжения. Точка 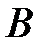 соответствует расстоянию
соответствует расстоянию 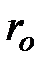 , на котором сила притяжения уравновешивает силу отталкивания. В этой точке значение потенциальной энергии минимальное. На рис. 3.3 видно, что кривая потенциальной энергии имеет характерный вид «потенциальной ямы». Наибольшая глубина потенциальной ямы соответствует расстоянию
, на котором сила притяжения уравновешивает силу отталкивания. В этой точке значение потенциальной энергии минимальное. На рис. 3.3 видно, что кривая потенциальной энергии имеет характерный вид «потенциальной ямы». Наибольшая глубина потенциальной ямы соответствует расстоянию 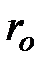 .
.
Кроме сил взаимодействия между молекулами реального газа необходимо учитывать также собственный объем молекул. Для идеального газа объем сосуда, в котором он находится, свободен для движения молекул реального газа, меньше геометрического объема сосуда на некоторую величину 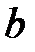 , которая представляет собой объем плотной упаковки молекул (рис. 3.4). В связи с этим, описывая состояние одного киломоля реального газа, вместо объема
, которая представляет собой объем плотной упаковки молекул (рис. 3.4). В связи с этим, описывая состояние одного киломоля реального газа, вместо объема 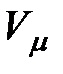 необходимо взять
необходимо взять  .
.
В молекулярно-кинетической теории идеального газа считается, что давление, которое оказывает газ на стенки сосуда, равно давлению, которое оказывают стенки сосуда на газ. Рассмотренное выше взаимодействие молекул реального газа приводит к возникновению некоторого добавочного давления  . Найдем величину этого давления, проводя следующие рассуждения.
. Найдем величину этого давления, проводя следующие рассуждения.
|
| Внутри объема газа любая молекула 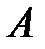 (рис. 3.5) взаимодействует со всеми молекулами, попадающими в сферу молекулярного действия. Таких молекул достаточно много, расположены они вокруг молекулы (рис. 3.5) взаимодействует со всеми молекулами, попадающими в сферу молекулярного действия. Таких молекул достаточно много, расположены они вокруг молекулы 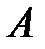 случайным образом, и равнодействующая всех сил, действующих на молекулу случайным образом, и равнодействующая всех сил, действующих на молекулу 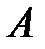 , будет равна нулю. Следовательно, внутри газа давление такое же, как если бы газ был идеальным. Молекулы же , будет равна нулю. Следовательно, внутри газа давление такое же, как если бы газ был идеальным. Молекулы же 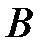 и и  , находящиеся вблизи стенки сосуда в слое толщиной, равной радиусу молекулярного действия, имеют с одной стороны от стенки больше «соседей», чем с другой. Равнодействующие сил, приложенные к молекулам , находящиеся вблизи стенки сосуда в слое толщиной, равной радиусу молекулярного действия, имеют с одной стороны от стенки больше «соседей», чем с другой. Равнодействующие сил, приложенные к молекулам 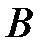 и и  , в связи с этим не равны нулю и направлены внутрь газа. , в связи с этим не равны нулю и направлены внутрь газа.
|
Равнодействующая сил, действующая на любую молекулу пограничного слоя, пропорциональна концентрации 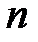 молекул в газе
молекул в газе  . Сумма сил, действующих на
. Сумма сил, действующих на 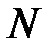 молекул газа в объеме параллелепипеда (рис. 3.6), построенного в пограничном слое на единичной площадке стенки сосуда, создает внутреннее давление
молекул газа в объеме параллелепипеда (рис. 3.6), построенного в пограничном слое на единичной площадке стенки сосуда, создает внутреннее давление
Следовательно, с учетом поправок на размеры молекул и на их взаимодействие (притяжение) состояние одного киломоля реального газа будет описываться уравнением:
или
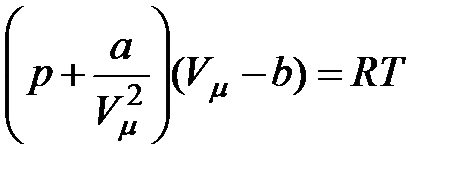
| (3.1)
|
|
| Уравнение (3.1) называется уравнением Ван-дер-Ваальса, а поправки  и и 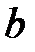 - поправки Ван-дер-Ваальса.
Для газа массой - поправки Ван-дер-Ваальса.
Для газа массой 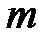 занимаемый объем равен занимаемый объем равен 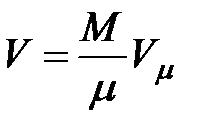 . Выразим отсюда объем . Выразим отсюда объем 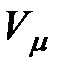 и подставим его в формулу (3.1). Получим: и подставим его в формулу (3.1). Получим:
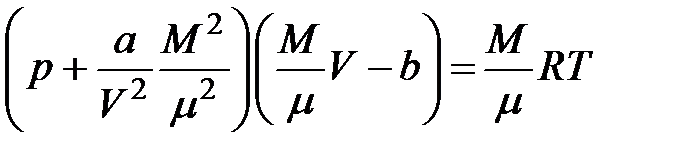
|
или
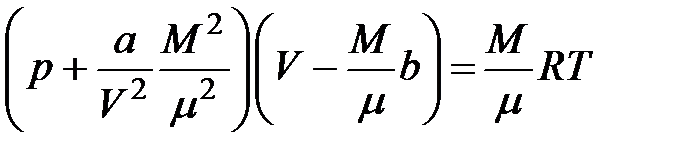
| (3.2)
|
Уравнение (3.2) есть уравнение состояния реального газа массой 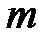 .
.
Дата добавления: 2015-08-11; просмотров: 791;
 от
от 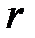 для любых молекул будет качественно одинаков: притяжение - на больших расстояниях и отталкивание – на малых. Важно заметить, что силы притяжения и отталкивания действуют одновременно, но в зависимости от расстояния между молекулами одна из них будет преобладающей. На расстоянии
для любых молекул будет качественно одинаков: притяжение - на больших расстояниях и отталкивание – на малых. Важно заметить, что силы притяжения и отталкивания действуют одновременно, но в зависимости от расстояния между молекулами одна из них будет преобладающей. На расстоянии 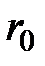 силы притяжения и отталкивания уравновешивают друг друга (рис. 3.2).
силы притяжения и отталкивания уравновешивают друг друга (рис. 3.2).
 соответствуют тому, что на малых расстояниях суммарная сила является силой отталкивания; ветвь
соответствуют тому, что на малых расстояниях суммарная сила является силой отталкивания; ветвь 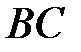 соответствует тому, что суммарная сила взаимодействия между молекулами на больших расстояниях является силой притяжения. Точка
соответствует тому, что суммарная сила взаимодействия между молекулами на больших расстояниях является силой притяжения. Точка 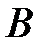 соответствует расстоянию
соответствует расстоянию 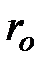 , на котором сила притяжения уравновешивает силу отталкивания. В этой точке значение потенциальной энергии минимальное. На рис. 3.3 видно, что кривая потенциальной энергии имеет характерный вид «потенциальной ямы». Наибольшая глубина потенциальной ямы соответствует расстоянию
, на котором сила притяжения уравновешивает силу отталкивания. В этой точке значение потенциальной энергии минимальное. На рис. 3.3 видно, что кривая потенциальной энергии имеет характерный вид «потенциальной ямы». Наибольшая глубина потенциальной ямы соответствует расстоянию 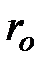 .
.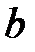 , которая представляет собой объем плотной упаковки молекул (рис. 3.4). В связи с этим, описывая состояние одного киломоля реального газа, вместо объема
, которая представляет собой объем плотной упаковки молекул (рис. 3.4). В связи с этим, описывая состояние одного киломоля реального газа, вместо объема 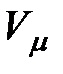 необходимо взять
необходимо взять  .
. . Найдем величину этого давления, проводя следующие рассуждения.
. Найдем величину этого давления, проводя следующие рассуждения.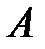 (рис. 3.5) взаимодействует со всеми молекулами, попадающими в сферу молекулярного действия. Таких молекул достаточно много, расположены они вокруг молекулы
(рис. 3.5) взаимодействует со всеми молекулами, попадающими в сферу молекулярного действия. Таких молекул достаточно много, расположены они вокруг молекулы 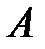 случайным образом, и равнодействующая всех сил, действующих на молекулу
случайным образом, и равнодействующая всех сил, действующих на молекулу 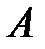 , будет равна нулю. Следовательно, внутри газа давление такое же, как если бы газ был идеальным. Молекулы же
, будет равна нулю. Следовательно, внутри газа давление такое же, как если бы газ был идеальным. Молекулы же 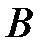 и
и  , находящиеся вблизи стенки сосуда в слое толщиной, равной радиусу молекулярного действия, имеют с одной стороны от стенки больше «соседей», чем с другой. Равнодействующие сил, приложенные к молекулам
, находящиеся вблизи стенки сосуда в слое толщиной, равной радиусу молекулярного действия, имеют с одной стороны от стенки больше «соседей», чем с другой. Равнодействующие сил, приложенные к молекулам 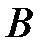 и
и  , в связи с этим не равны нулю и направлены внутрь газа.
, в связи с этим не равны нулю и направлены внутрь газа.
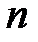 молекул в газе
молекул в газе  . Сумма сил, действующих на
. Сумма сил, действующих на 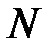 молекул газа в объеме параллелепипеда (рис. 3.6), построенного в пограничном слое на единичной площадке стенки сосуда, создает внутреннее давление
молекул газа в объеме параллелепипеда (рис. 3.6), построенного в пограничном слое на единичной площадке стенки сосуда, создает внутреннее давление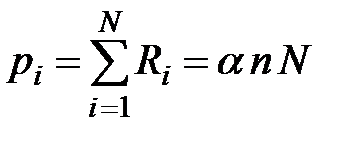
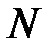 в объеме параллелепипеда также пропорционально концентрации молекул
в объеме параллелепипеда также пропорционально концентрации молекул 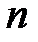 :
:  . Тогда внутреннее давление
. Тогда внутреннее давление
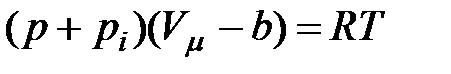
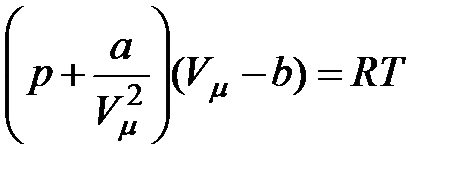
 и
и 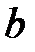 - поправки Ван-дер-Ваальса.
Для газа массой
- поправки Ван-дер-Ваальса.
Для газа массой 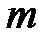 занимаемый объем равен
занимаемый объем равен 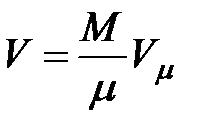 . Выразим отсюда объем
. Выразим отсюда объем 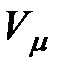 и подставим его в формулу (3.1). Получим:
и подставим его в формулу (3.1). Получим:
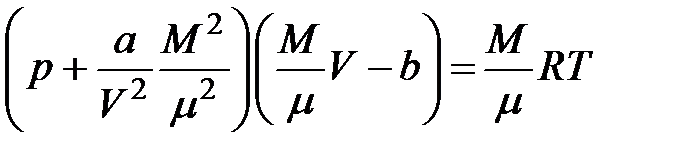
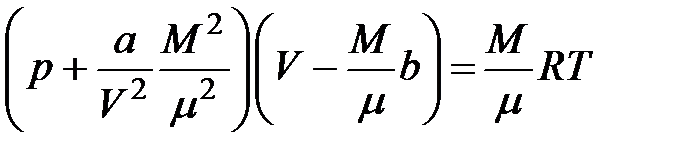
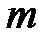 .
.
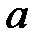
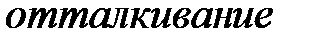
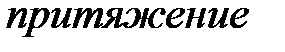
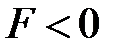
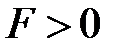
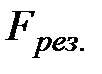
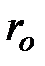

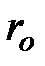



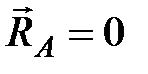
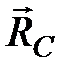
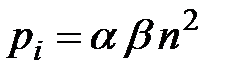
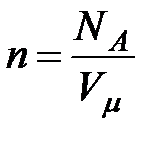 (
( 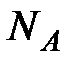 - число Авогадро). Константы
- число Авогадро). Константы 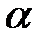 и
и 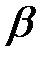 зависят от природы газа. Обозначив произведение
зависят от природы газа. Обозначив произведение 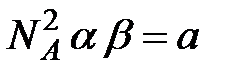 , получим
, получим