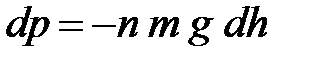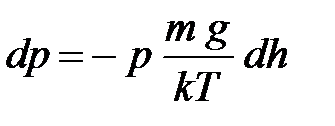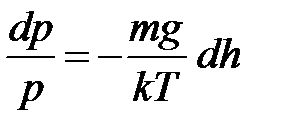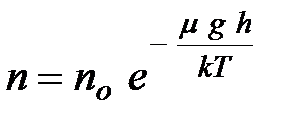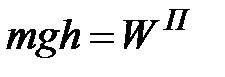Распределение молекул газа в потенциальном поле сил (распределение Больцмана). Барометрическая формула.
Если на молекулы газа не действуют внешние силы, то благодаря хаотичному движению они равномерно распределяются по всему предоставленному им объему.
Рассмотрим газ, находящийся в однородном потенциальном поле сил, например, в поле тяготения вблизи поверхности Земли. Действие силы тяжести препятствует молекулам атмосферного воздуха, окружающего Землю, разлететься по вселенному пространству. В то же время тепловое движение не позволяет молекулам воздуха скапливаться у поверхности Земли, где их потенциальная энергия минимальна. Наличие этих двух противоположных тенденций способствует установлению в атмосфере вполне определенного распределения молекул по высоте над поверхностью Земли. Найдем это распределение.
Рассмотрим вертикальный столб воздуха с основанием  (рис. 2.6).
(рис. 2.6).
Для упрощения вывода будем считать ускорение силы тяжести и температуру воздуха постоянными, не зависящими от высоты. Обозначим давление воздуха на высоте 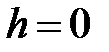 через
через 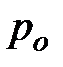 , а на высоте
, а на высоте  - через
- через 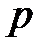 . При изменении высоты на
. При изменении высоты на 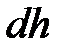 давление изменяется на величину
давление изменяется на величину 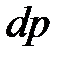 , причем, если
, причем, если 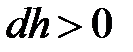 , то
, то 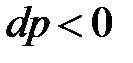 ( так как давление с высотой убывает).
( так как давление с высотой убывает).
Давление 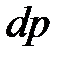 найдем как вес столба воздуха над площадкой
найдем как вес столба воздуха над площадкой  высотой
высотой 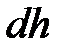 . Если средняя концентрация молекул воздуха на высоте между
. Если средняя концентрация молекул воздуха на высоте между  и
и 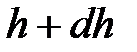 равна
равна 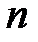 , то вес столба воздуха высотой
, то вес столба воздуха высотой 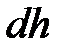 с основанием
с основанием 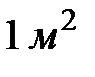 равен
равен
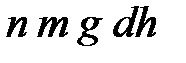 , ,
|
где 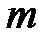 - масса одной молекулы,
- масса одной молекулы,
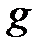 - ускорение силы тяжести.
- ускорение силы тяжести.
| Найдем разность давлений:
Из уравнения (1.16) выразим
откуда
|
Интегрируем, имея в виду, что 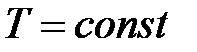 и
и 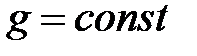 :
:
 или или 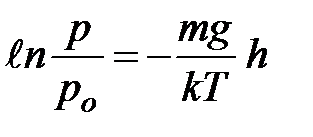
|
или
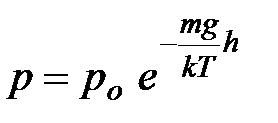
| (2.11) |
Формула (2.11) называется барометрической. Она устанавливает закон изменения давления с высотой и позволяет вычислить давление атмосферы на высоте  или наоборот, измерив давление, определить высоту.
или наоборот, измерив давление, определить высоту.
Приборы, предназначенные для измерения высоты полета самолета, горных вершин и т.д., называются высотомерами. Они представляют собой специальные барометры, шкала которых проградуирована в метрах. Однако, в формулу (2.11) в этом случае вносят поправки, связанные с изменением температуры 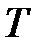 и ускорения свободного падения
и ускорения свободного падения 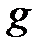 с высотой.
с высотой.
Так как 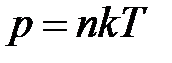 , то уравнение (2.11) можно переписать следующим образом:
, то уравнение (2.11) можно переписать следующим образом:
 , ,
| (2.12) |
где 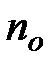 - число молекул в единице объема на высоте
- число молекул в единице объема на высоте 
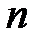 - число молекул в единице объема на высоте
- число молекул в единице объема на высоте 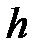
Уравнение (2.12) показывает, как изменяется с высотой концентрация молекул (число молекул в единице объема).
Из формул (2.11) и (2.12) видно, что с высотой давление 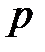 и концентрация молекул
и концентрация молекул 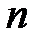 убывает по экспоненциальному закону. Графически это представлено на рис. 2.7.
убывает по экспоненциальному закону. Графически это представлено на рис. 2.7.
Формулу (2.12) можно преобразовать, если вместо массы молекулы 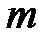 ввести молярную массу газа
ввести молярную массу газа  . Тогда, используя равенства
. Тогда, используя равенства
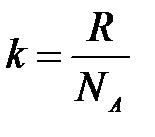 и и 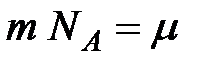
|
| получим:
Анализируя уравнение (2.12), можно заметить, что величина
Представляет собой потенциальную энергию молекулы в поле силы тяжести на высоте
| |||||||||||
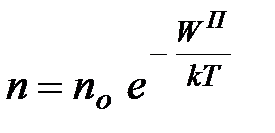
| (2.14) | |||||||||||
где  - концентрация молекул в том месте атмосферы, где потенциальная энергия
- концентрация молекул в том месте атмосферы, где потенциальная энергия 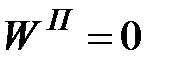 .
.
Последняя формула дает распределение молекул по величине потенциальной энергии и называется распределением Больцмана. Она справедлива для поля любых потенциальных сил.
Дата добавления: 2015-08-11; просмотров: 1815;




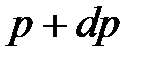
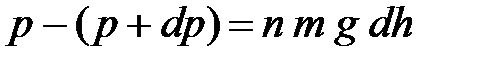 или
или