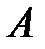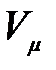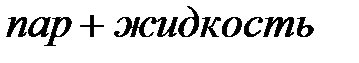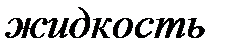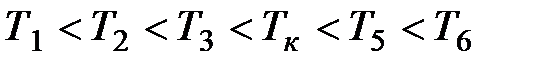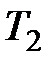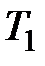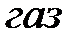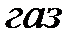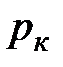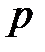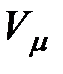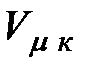Сжижение газа.
В уравнении (3.1) Ван-дер-Ваальса раскроем скобки и перенесем все его члены в левую часть. Получим уравнение третьей степени относительно молярного объема:
Коэффициенты уравнения зависят от давления, температуры и химической природы газа. В зависимости от численных значений 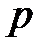 и
и 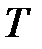 для данного газа это уравнение может иметь либо один, либо три вещественных корня. На рис. 3.7 изображена одна из изотерм Ван-дер-Ваальса (теоретическая изотерма).
для данного газа это уравнение может иметь либо один, либо три вещественных корня. На рис. 3.7 изображена одна из изотерм Ван-дер-Ваальса (теоретическая изотерма).
На рис. 3.8 изображена изотерма, полученная экспериментально при исследовании углекислого газа. Теоретическая изотерма имеет вид кривой 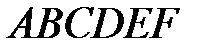 , экспериментальная изотерма изображена в виде ломаной линии
, экспериментальная изотерма изображена в виде ломаной линии 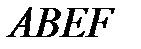 . Участок
. Участок 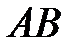 теоретической и экспериментальной изотерм соответствует газообразному состоянию вещества, участок
теоретической и экспериментальной изотерм соответствует газообразному состоянию вещества, участок 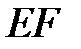 - жидкому состоянию, которому свойственна очень малая сжимаемость. Горизонтальный участок
- жидкому состоянию, которому свойственна очень малая сжимаемость. Горизонтальный участок 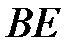 соответствует переходу газа в жидкость (конденсация), который при данной температуре происходит при постоянном давлении (давление насыщенных паров). Сравнивая рис. 3.7 и 3.8, видим, что различие между теоретической и экспериментальной изотермами реальных газов при относительно низких температурах сводится к тому, что волнообразный участок теоретической изотермы заменяется горизонтальным участком в экспериментальной изотерме.
соответствует переходу газа в жидкость (конденсация), который при данной температуре происходит при постоянном давлении (давление насыщенных паров). Сравнивая рис. 3.7 и 3.8, видим, что различие между теоретической и экспериментальной изотермами реальных газов при относительно низких температурах сводится к тому, что волнообразный участок теоретической изотермы заменяется горизонтальным участком в экспериментальной изотерме.
Однако оказывается, что при определенных условиях можно осуществить на опыте некоторые участки волнообразной кривой теоретической изотермы. Если подвергаемый сжатию газ тщательно очистить от пыли, то можно наблюдать задержку возникновения конденсации. Это состояние изображается участком  и соответствует пересыщенному пару, когда количество пара больше, чем необходимо для того, чтобы он был насыщающим. Но это состояние неустойчиво, и в веществе самопроизвольно из-за флуктуаций плотности возникает конденсация.
и соответствует пересыщенному пару, когда количество пара больше, чем необходимо для того, чтобы он был насыщающим. Но это состояние неустойчиво, и в веществе самопроизвольно из-за флуктуаций плотности возникает конденсация.
Еще менее устойчивым является состояние, изображенное участком  . Это состояние вещества называют растянутой или перегретой жидкостью. Его можно осуществить, если задержать кипение жидкости, тщательно удалив из нее пузырьки пара и примеси.
. Это состояние вещества называют растянутой или перегретой жидкостью. Его можно осуществить, если задержать кипение жидкости, тщательно удалив из нее пузырьки пара и примеси.
Участок 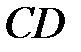 изображает совершенно неустойчивое состояние, так как ему соответствует необычная зависимость объема от давления (с увеличением давления объем не уменьшается, а увеличивается). Такое состояние на опыте не наблюдается.
изображает совершенно неустойчивое состояние, так как ему соответствует необычная зависимость объема от давления (с увеличением давления объем не уменьшается, а увеличивается). Такое состояние на опыте не наблюдается.
На рис. 3.9 изображены изотермы Ван-дер-Ваальса при разных температурах. Из графика видно, что с повышением температуры волнообразный участок изотерм уменьшается, т.е. уменьшается разница между молярным объемом насыщенного пара и жидкости. При некоторой температуре, называемой критической температурой 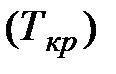 , этот участок изотермы исчезает совсем и наблюдается только точка перегиба
, этот участок изотермы исчезает совсем и наблюдается только точка перегиба 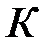 , которая называется критической точкой. При более высоких температурах изотермы Ван-дер-Ваальса напоминают изотермы идеальных газов.
, которая называется критической точкой. При более высоких температурах изотермы Ван-дер-Ваальса напоминают изотермы идеальных газов.
Если соединить между собой правые концы горизонтальных участков экспериментальных изотерм, то полученная кривая 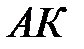 будет указывать на уменьшение молярного объема насыщенного пара с увеличением температуры, вплоть до критической.
будет указывать на уменьшение молярного объема насыщенного пара с увеличением температуры, вплоть до критической.
Соединив между собой левые концы горизонтальных участков экспериментальных изотерм, получим кривую 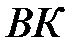 , изображающую зависимость от температуры молярного объема жидкости, который увеличивается с возрастанием температуры.
, изображающую зависимость от температуры молярного объема жидкости, который увеличивается с возрастанием температуры.
При критической температуре молярный объем жидкости становится равным молярному объему пара. В этом случае исчезает разница между жидким и газообразным состоянием вещества. Такое состояние называется критическим. На эту особенность вещества впервые указал Д.И.Менделеев.
|
| Критическая изотерма и кривая  делят диаграмму состояния на три области: справа от делят диаграмму состояния на три области: справа от 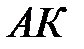 вещество находится в газообразном состоянии; слева от вещество находится в газообразном состоянии; слева от 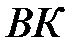 - жидкость; в области, ограниченной кривой - жидкость; в области, ограниченной кривой  , вещество находится в двух фазах – жидкость и пар. , вещество находится в двух фазах – жидкость и пар.
|
Из приведенной диаграммы состояния следует, что никаким сжатием газообразного вещества при температурах выше критической нельзя превратить его в жидкость. Для того, чтобы перевести газ в жидкое состояние сжатием, его нужно охладить до температуры, ниже критической.
Критической точке соответствуют также критические давление 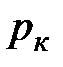 и критический объем
и критический объем 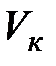 . Критические параметры зависят от природы вещества; с поправками Ван-дер-Ваальса
. Критические параметры зависят от природы вещества; с поправками Ван-дер-Ваальса 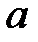 и
и 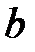 они связаны следующими соотношениями:
они связаны следующими соотношениями:
где 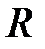 - универсальная газовая постоянная.
- универсальная газовая постоянная.
Дата добавления: 2015-08-11; просмотров: 835;
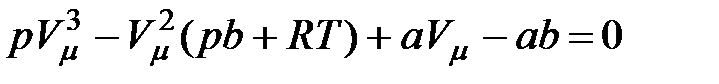
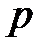 и
и 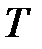 для данного газа это уравнение может иметь либо один, либо три вещественных корня. На рис. 3.7 изображена одна из изотерм Ван-дер-Ваальса (теоретическая изотерма).
для данного газа это уравнение может иметь либо один, либо три вещественных корня. На рис. 3.7 изображена одна из изотерм Ван-дер-Ваальса (теоретическая изотерма).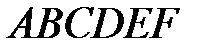 , экспериментальная изотерма изображена в виде ломаной линии
, экспериментальная изотерма изображена в виде ломаной линии 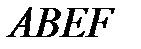 . Участок
. Участок 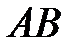 теоретической и экспериментальной изотерм соответствует газообразному состоянию вещества, участок
теоретической и экспериментальной изотерм соответствует газообразному состоянию вещества, участок 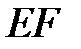 - жидкому состоянию, которому свойственна очень малая сжимаемость. Горизонтальный участок
- жидкому состоянию, которому свойственна очень малая сжимаемость. Горизонтальный участок 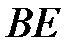 соответствует переходу газа в жидкость (конденсация), который при данной температуре происходит при постоянном давлении (давление насыщенных паров). Сравнивая рис. 3.7 и 3.8, видим, что различие между теоретической и экспериментальной изотермами реальных газов при относительно низких температурах сводится к тому, что волнообразный участок теоретической изотермы заменяется горизонтальным участком в экспериментальной изотерме.
соответствует переходу газа в жидкость (конденсация), который при данной температуре происходит при постоянном давлении (давление насыщенных паров). Сравнивая рис. 3.7 и 3.8, видим, что различие между теоретической и экспериментальной изотермами реальных газов при относительно низких температурах сводится к тому, что волнообразный участок теоретической изотермы заменяется горизонтальным участком в экспериментальной изотерме. и соответствует пересыщенному пару, когда количество пара больше, чем необходимо для того, чтобы он был насыщающим. Но это состояние неустойчиво, и в веществе самопроизвольно из-за флуктуаций плотности возникает конденсация.
и соответствует пересыщенному пару, когда количество пара больше, чем необходимо для того, чтобы он был насыщающим. Но это состояние неустойчиво, и в веществе самопроизвольно из-за флуктуаций плотности возникает конденсация. . Это состояние вещества называют растянутой или перегретой жидкостью. Его можно осуществить, если задержать кипение жидкости, тщательно удалив из нее пузырьки пара и примеси.
. Это состояние вещества называют растянутой или перегретой жидкостью. Его можно осуществить, если задержать кипение жидкости, тщательно удалив из нее пузырьки пара и примеси.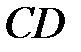 изображает совершенно неустойчивое состояние, так как ему соответствует необычная зависимость объема от давления (с увеличением давления объем не уменьшается, а увеличивается). Такое состояние на опыте не наблюдается.
изображает совершенно неустойчивое состояние, так как ему соответствует необычная зависимость объема от давления (с увеличением давления объем не уменьшается, а увеличивается). Такое состояние на опыте не наблюдается.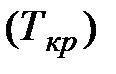 , этот участок изотермы исчезает совсем и наблюдается только точка перегиба
, этот участок изотермы исчезает совсем и наблюдается только точка перегиба 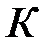 , которая называется критической точкой. При более высоких температурах изотермы Ван-дер-Ваальса напоминают изотермы идеальных газов.
, которая называется критической точкой. При более высоких температурах изотермы Ван-дер-Ваальса напоминают изотермы идеальных газов.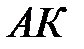 будет указывать на уменьшение молярного объема насыщенного пара с увеличением температуры, вплоть до критической.
будет указывать на уменьшение молярного объема насыщенного пара с увеличением температуры, вплоть до критической.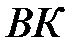 , изображающую зависимость от температуры молярного объема жидкости, который увеличивается с возрастанием температуры.
, изображающую зависимость от температуры молярного объема жидкости, который увеличивается с возрастанием температуры. делят диаграмму состояния на три области: справа от
делят диаграмму состояния на три области: справа от 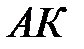 вещество находится в газообразном состоянии; слева от
вещество находится в газообразном состоянии; слева от 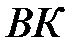 - жидкость; в области, ограниченной кривой
- жидкость; в области, ограниченной кривой  , вещество находится в двух фазах – жидкость и пар.
, вещество находится в двух фазах – жидкость и пар.
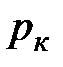 и критический объем
и критический объем 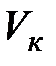 . Критические параметры зависят от природы вещества; с поправками Ван-дер-Ваальса
. Критические параметры зависят от природы вещества; с поправками Ван-дер-Ваальса 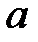 и
и 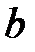 они связаны следующими соотношениями:
они связаны следующими соотношениями: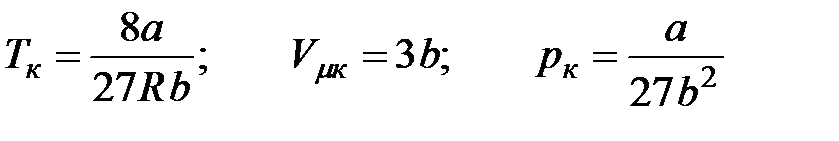
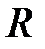 - универсальная газовая постоянная.
- универсальная газовая постоянная.