Глава 14. Термодинамические свойства реального газа. Летучесть.
14.1. Постановка проблемы.
То, что реальные газы при увеличении давления перестают подчиняться уравнению состояния идеального газа 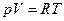 -это не самая главная проблема, а дело в том, что при температуре ниже некоторой критической реальные газы при соответствующем повышении давления конденсируются в жидкость, иными словами система становится гетерогенной. Уравнений состояния таких флюидных систем (флюидные – системы, включающие газообразную и жидкую фазу или одну из них) известно более двухсот, но наиболее популярное и позволяющее понять суть дела это уравнение состояния газа Ван-дер-Ваальса (1873) для одного моля газа
-это не самая главная проблема, а дело в том, что при температуре ниже некоторой критической реальные газы при соответствующем повышении давления конденсируются в жидкость, иными словами система становится гетерогенной. Уравнений состояния таких флюидных систем (флюидные – системы, включающие газообразную и жидкую фазу или одну из них) известно более двухсот, но наиболее популярное и позволяющее понять суть дела это уравнение состояния газа Ван-дер-Ваальса (1873) для одного моля газа
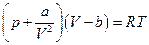
или для «п» молей газа, занимающих объем V
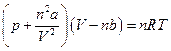
где «а» и «b» - некоторые константы, зависящие от свойств данного газа.
Для индивидуального газа энергия Гиббса в зависимости от давления при данной температуре вычисляется сравнительно просто : если газ идеальный , то (см. гл. 8) 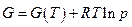
Если газ подчиняется уравнению Ван-дер-Ваальса, то, во-первых,
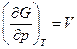
во-вторых, из уравнения состояния

и, следовательно, при T = const

Взятие неопределенного интеграла при постоянной температуре дает (константа интегрирования будет функцией температуры)
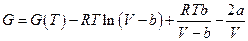
Если имеем идеально-газовую смесь, то химический потенциал компонента i в такой смеси :
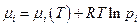
Это следствие того факта, что объем идеально-газовой смеси равен сумме объемов газов до смешения (закон Дальтона, см. гл.8) и кроме того мы очень легко можем составить уравнения для характеристических функций смеси идеальных газов.
Уравнение состояния смеси реальных газов, например, подчиняющихся уравнению состояния Ван-дер-Ваальса в первом приближении можно представить следующим образом
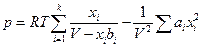
где ai и bi – константы уравнения Ван-дер-Ваальса i –ого газа, xi –его мольная доля в смеси.
Легко заметить, что получение в явном виде выражения для химического потенциала i –ого газа становится не простой задачей и, кроме того, при условии справедливости уравнения Ван-дер-Ваальса. Иными словами пока не удается найти общее и достаточно простое решение задачи.
Зададимся следующим вопросом : а что мы можем экспериментально измерить, имея реальный газ? Очевидно, это будут его температура, его давление, его объем и работа, которую он совершает при изотермическом равновесном изменении объема
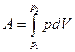
Если газ идеальный, то (см. гл.2) работа изотермического изменения объема (давления) легко вычисляется :
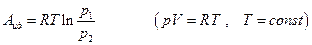
Дата добавления: 2015-07-30; просмотров: 1184;
