Глава 12. Растворы электролитов – термодинамика.
12.1. Электролитическая диссоциация.
В электролитах – проводниках второго рода – перенос электричества сопровождается переносом вещества, таким образом электролитами являются не только растворы, но и расплавы и твердые вещества. Но растворы электролитов обладают особыми коллигативными свойствами : необходимо в уравнения для них вводить поправочный изотонический коэффициент Вант-Гоффа, который показывает, что число частиц в растворе больше, чем было введено молекул растворенного вещества. Это обстоятельство, а также тот факт, что эти растворы электропроводны, позволили Аррениусу (в 1883 – 1887 годах) разработать теорию электролитической диссоциации, которая основана на трех постулатах:
1. Некоторые вещества обладают способностью при растворении в соответствующих растворителях распадаться на противоположно заряженные частицы – ионы, которые состоят или из отдельных атомов, или из группы атомов.
2. Диссоциация молекул на ионы является неполной и характеризуется степенью диссоциации α. Если молекула дает ν ионов, то изотонический коэффициент Вант-Гоффа i = 1 + α (ν – 1).
3. Силы взаимодействия между ионами отсутствуют и растворы электролитов ведут себя подобно идеальным газовым системам. Это положение прямо не высказывалось, но оно лежит в основе всех количественных соотношений, полученных авторами теории электролитической диссоциации.
Для бинарного электролита КА с концентрацией с константа диссоциации К и степень диссоциации α связаны отношением

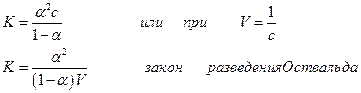
На основании теории Аррениуса была сформулирована первая теория кислот и оснований, которая была широко применена к трактовке кислотно-основных равновесий, введено понятие о ионном произведении воды и объяснены явления гидролиза, показана возможность расчета кривых нейтрализации, а также буферной емкости растворов, сформулировано понятие о произведении растворимости и объяснено уменьшение растворимости при добавлении в раствор веществ, имеющих общий ион с малорастворимой солью, а также увеличение растворимости за счет комплексообразования.
За теорию электролитической диссоциации в 1903 году Сванте Хенрик Аррениус получил Нобелевскую премию.
12.2.Причины электролитической диссоциации.
Теория Аррениуса имеет два существенных недостатка. Во-первых, не учитывается взаимодействие ионов с диполями воды, которое является физической основой образования ионов в растворе при растворении электролита, т.е. без учета ион-дипольного взаимодействия нельзя объяснить процесс образования ионов и устойчивость ионных систем. Во-вторых, игнорируется ион-ионное взаимодействие, ионы рассматривались как частицы идеального газа, а, следовательно,не учитывалось притяжение катионов и анионов и отталкивание одноименно заряженных ионов. Это приводит к непостоянству константы диссоциации, а также к тому, что степени диссоциации, полученные с помощью коллигативных свойств растворов, с помощью измерений электропроводности и с помощью измерений методами электрохимической термодинамики, отличаются друг от друга.
Термин «электролитическая диссоциация» подразумевает образование ионов в растворе при распаде нейтральных молекул растворяемого вещества. Однако часто ионы существуют уже до растворения (такие вещества иногда называют ионофорами), например, NaCl, при растворении которого происходит разрушение кристалла за счет взаимодействия ионов с диполями растворителя. Чтобы доказать это нужно сопоставить энергию разрушения кристаллической решетки с энергией сольватации. Если эти величины одного порядка, то вывод о разрушении соли за счет ион-дипольного взаимодействия можно считать правильным.
В ряде случаев раствор электролита действительно получается при растворении вещества, состоящего из нейтральных молекул (такие вещества называют ионогенами). Например, при растворении в воде хлористого водорода получается соляная кислота. Однако и здесь происходит взаимодействие молекул HCl с молекулами воды:
HCl + H2O → H3O+ + Cl -
и образовавшиеся ионы в свою очередь вступают в ион-диполньное взаимодействие с избыточными молекулами воды. Таким образом, энергия, необходимая для разрыва связи H — Cl (432 кДж/моль), компенсируется энергией связи протона с молекулой воды в ионе Н3О+ и Cl -. Тоже самое относится и к аммиаку :
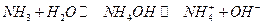
Энергия кристаллической решетки представляет собой работу разведения составляющих ее ионов на бесконечно большое расстояние в вакууме.
С помощью законов электростатики М.Борн получил следующую формулу
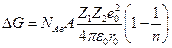
где NАв –число Авогадро, А – константа Маделунга, зависящая от типа кристаллической решетки, Z1 и Z2 – валентности катиона и аниона, е0 – заряд электрона, ε0 – диэлектрическая постоянная вакуума, r0 – сумма радиусов катиона и аниона, п –показатель степени, в которую возводится расстояние между ионами при расчете силы отталкивания между ионами (5 ≤ п ≤12). Для NaCl,, например, A = 1,7476, n =7,5, r0 =(0,95 + 1,81) нм и∆GNaCl =762 кДж/моль. Эту величину интересно сопоставить с изменением энтальпии в ходе разрушения кристаллической решетки хлорида натрия ∆НNaCl с помощью следующего термодинамического цикла :
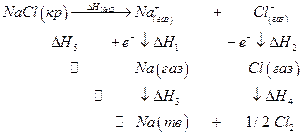
Значение ∆ Н1 можно приравнять потенциалу ионизации натрия, взятому с обратным знаком. ∆ Н2 определяется сродством к электрону атома хлора. ∆ Н3 – тепловой эффект конденсации паров натрия, ∆ Н4 – тепловой эффект рекомбинации атомов хлора, а ∆ Н5 – тепловой эффект при сжигании металлического натрия в хлоре. Численно эти величины равны ∆Н1 = -496; ∆ Н2 = 365; ∆ Н3 = -109; ∆ Н4 =-121; ∆ Н5 = -411 кДж/моль. По закону Гесса
∆HNaCl = -(∆Н1 + ∆Н2 + ∆Н3 + ∆Н4 + ∆Н5 ) = 772 кДж/моль
Вклад T∆S при 25 0С составляет величину примерно 15 кДж/моль, и тогда получаем ∆GNaCl = 757 кДж/моль, что чрезвычайно близко к теоретической величине, приведенной выше.
Энергия сольватации представляет собой выигрыш в энергии, который получается при перенесении моля ионов из вакуума в данный растворитель. Очевидно, для сохранения электронейтральности вносить нужно одновременно катионы и анионы. М.Борн разработал следующую простую модель, согласно которой ион рассматривается как заряженный шарик радиуса ri , а растворитель как сплошная однородная среда с диэлектрической постоянной ε, а сам процесс разбивается на три этапа 1) разряд шарика в вакууме; 2) перенос незаряженного шарика из вакуума в растворитель; 3) заряжение шарика в среде. Предполагается, что работа на 2 этапе равна нулю, а работы 1 и 3 этапа могут быть рассчитаны по законам электростатики. В итоге Борн получил :
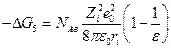
Энергии гидратации, рассчитанные по модели Борна, весьма велики и достаточны для разрушения кристаллической решетки при образовании растворов электролитов. (Для NaCl энтальпия гидратации по Борну равна – 1121 кДж/моль ) Если в формулах Борна пренебречь 1/п и 1/ε по сравнению с единицей, положить Z1=Z2 , А ≈ 2 и ri =r0 /2, то энергия сольватации одного иона окажется равной половине энергии кристаллической решетки, т.е. энергия сольватации двух ионов – катиона и аниона – как раз компенсирует энергию разрушения решетки кристалла.
Экспериментальную величину энергии сольватации можно получить с помощью следующего цикла :
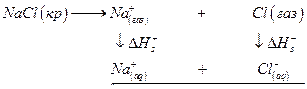
где 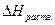 - тепловой эффект растворения в бесконечно разбавленном растворе. Тогда тепловой эффект сольватации
- тепловой эффект растворения в бесконечно разбавленном растворе. Тогда тепловой эффект сольватации
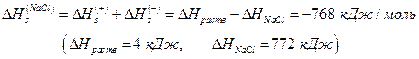
Более сложные модели позволяют устранить различие между расчетными и экспериментальными величинами энтальпии сольватации.
12.3. Ион-ионное взаимодействие в растворах электролитов.
Ион-дипольное взаимодействие позволяет объяснить образование и устойчивость растворов электролитов. Однако для количественного описания термодинамических свойств этих растворов необходимо учитывать также ион-ионное взаимодействие. Для этого проведем некоторую предварительную подготовку проблемы. Обозначим индексами 1 и 2 свойства растворителя и электролита соответственно. Если раствор бинарный, то по уравнению Гиббса-Дюгема:
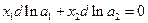
Если для катиона и аниона;

и для раствора в целом
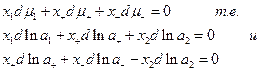
Если электролит 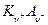 диссоциирует по реакции:
диссоциирует по реакции:
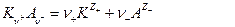 , то
, то
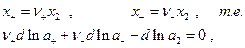
следовательно
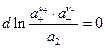
иными словами 
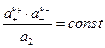
Стандартное состояние выбираем так.
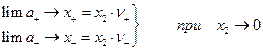
а стандартное состояние для а2 выбираем так, чтобы const = 1, т.е.
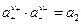
Поскольку активности ионов изолировано определить невозможно, введем определение средней ионной активности :
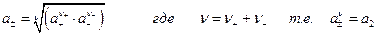
Далее 

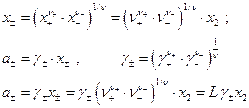
Величина 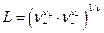 зависит от валентного типа электролита.
зависит от валентного типа электролита.
| Тип электролита | Пример | L |
| 1-1, 2-2,3-3 | KCl, ZnSO4, LaFe(CN)6 | |
| 2-1 1-2 | CaCl2 Na2SO4 | 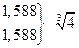
|
| 3-1 1-3 | LaCl3 K3Fe(CN)6 | 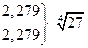
|
| 4-1 1-4 | Th(NO3)4 K4Fe(CN)6 | 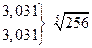
|
| 3-2 | Al2(SO4)3 | 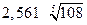
|
Ранее уже отмечалось, что RT lnγ представляет собой работу переноса 1 моля компонента из идеального раствора в данный реальный раствор. Чтобы описать ион-ионное взаимодействие , необходимо знать распределение ионов в растворе и природу сил, действующих между ионами. Поскольку и ионы, и диполи растворителя находятся в хаотическом движении и могут образовывать ассоциаты, то задача о распределении ионов оказывается весьма сложной. Можно предположить, что электролит полностью диссоциирован ( α = 1 ), растворитель представляет собой непрерывную среду с диэлектрической постоянной ε, а ионы взаимодействуют только по закону Кулона. Дебай и Гюккель (1923) предложили следующую модель. Среди множества ионов выбирается центральный ион, который окружен ионной атмосферой. Тепловое движение ионов как бы размазывает дискретные заряды, и ионную атмосферу можно моделировать облаком размазанного заряда, плотность которого ρ уменьшается по мере удаления от центрального иона. Общий заряд ионной атмосферы в силу электронейтральности раствора по абсолютной величине равен заряду центрального иона Zie0 и противоположен ему по знаку.
Поскольку ионная атмосфера обладает шаровой симметрией, то объемная плотность заряда ρ и потенциал φ на расстоянии r от центрального иона связаны уравнением Пуассона в сферических координатах
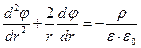
Если распределение ионов в ионной атмосфере подчиняется уравнению Больцмана, то
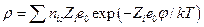
и после разложения в ряд экспоненты при условии 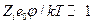 имеем
имеем
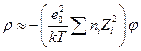 ,
,
т.к. из-за электронейтральности 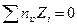 , где nio – объемная концентрация i – ого иона. Тогда уравнение Пуассона приводится к виду
, где nio – объемная концентрация i – ого иона. Тогда уравнение Пуассона приводится к виду
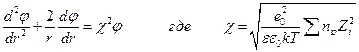
Решение диффернциального уравнения при условии, что ион является материальной точкой, позволяет вычислить потенциал, создаваемый ионной атмосферой в месте расположения центрального иона
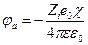
Это уравнение показывает, что ионная атмосфера оказывает на центральный ион такое же влияние, какое оказывала бы на него тонкая сферическая оболочка, имеющая заряд –Zie0 и расположенная на расстоянии 1/χ от точечного центрального иона, или же взаимодействие центрального иона с ионной атмосферой можно свести к кулоновскому взаимодействию двух ионов с зарядами Zie0 и –Zie0 , находящихся друг от друга на расстоянии 1/χ. Таким образом изменение энергии центрального иона за счет его взаимодействия с ионной атмосферой составляет
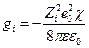
следовательно коэффициент активности отдельного иона будет
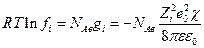
а с учетом 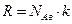 и выражения для χ
и выражения для χ
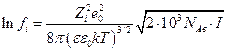
где 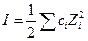 ионная сила раствора.
ионная сила раствора.
Подстановка констант дает :
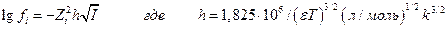
Для среднего коэффициента активности
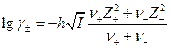
а по условию электронейтральности 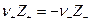 Следовательно
Следовательно
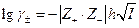
Это уравнение позволяет объяснить ряд экспериментальных результатов, которые были известны еще до создания теории Дебая-Гюккеля. Бренстедом было обнаружено, что для растворов 1-1 валентных элетролитов при
с ≤ 0,01 моль/л выполняется эмпирическое соотношение 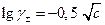
По Дебаю и Гюккелю при 20 0С
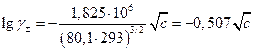
Далее, коэффициенты активности в растворах с одинаковой ионной силой должны быть одинаковыми и это согласуется с законом Льюиса и Рендалла, который был открыт раньше. Справедливость модели ДебаяГюккеля только для разбавленных растворов обусловлена следующими причинами :
1. Предположение, что заряд ионов размазан в ионной атмосфере, выполняется только, когда можно пренебречь собственным объемом ионов, т.е в разбавленных растворах, и только в этих условиях справедливо уравнение Пуассона.
2. Распределение Больцмана с дополнительным условием 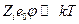 также справедливо только в разбавленных растворах.
также справедливо только в разбавленных растворах.
3. Не учитывается изменение диэлектрической проницаемости раствора.
4. Ионы рассматриваются как материальные точки, что справедливо только в разбавленных растворах.
5. Учитывается только кулоновское взаимодействие и игнорируются другие виды взаимодействия (ион-дипольное, образование ассоциатов, комплексов и т.п.).
Во втором приближении Дебай и Гюккель учли собственные размеры ионов :
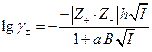
где а по своему физическому смыслу соответствует расстоянию, до которого могут сближаться электрические центры двух ионов, однако сольватация делает эту величину неопределенной, поэтому она подбирается по экспериментальным данным, а
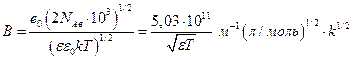
Сравним 1 и 2 приближение для NaCl ( а=0,48 нм ) при 25 0С
| m | 0,001 | 0,005 | 0,01 | 0,05 | 0,1 |
| -lg γ±, эксп. | 0,0155 | 0,0327 | 0,0446 | 0,0859 | 0,1072 |
| -lgγ±, I прибл. | 0,0162 | 0,0362 | 0,0511 | 0,1162 | 0,1674 |
| -lg γ±, II прибл. | 0,0154 | 0,0325 | 0,0441 | 0,0844 | 0,1077 |
Для более высоких концентраций можно предложить следующую форму уравнения :
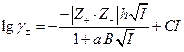
эмпирическим подбором а и С можно описать экспериментальные данные до т порядка 1 ÷ 2, однако константа С лишена определенного физического смысла.
12.4. Применение теории Дебая-Гюккеля к слабым электролитам.
Для электролита СА, диссоциирующего по схеме 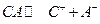 , термодинамическая константа диссоциации
, термодинамическая константа диссоциации
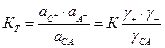
где К – кажущаяся константа диссоциации. Так как
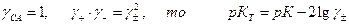
Если степень диссоциации α, то ионная сила 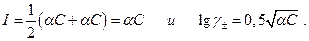
Таким образом 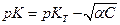
т.е. рК зависит от концентрации слабого электролита.
Подстановка активностей вместо концентрации необходима и при записи выражений для ионного произведения воды, произведения растворимости, констант ассоциации комплексных соединений и др.
12.5. Растворимость и теория Дебая-Гюккеля.
Если малорастворимая соль полностью диссоциирована, то произведение растворимости в чистом растворителе
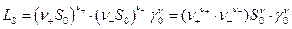
где S0 – растворимость, γ0 –средний коэффициент активности.
Для 1,1 – валентной соли 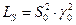
Если в раствор добавлена соль, не содержащая общих ионов с малорастворимой солью, то 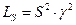
отсюда 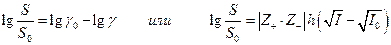
где I0 – ионная сила одной малорастворимой соли, I – ионная сила в присутствии постороннего электролита. Так как при постоянной температуре I0 =const , то теория предсказывает линейную зависимость между 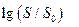 и
и 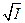 с наклоном
с наклоном 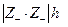 , что и наблюдалось экспериментально.
, что и наблюдалось экспериментально.
Глава 13. Гетерогенное равновесие многокомпонентных систем без химических реакций.
13.1. Правило фаз Гиббса.
Легко сообразить, что если гомогенная однокомпонентная система находится в равновесии, то ее состояние описывается заданием значений двух независимых переменных, поскольку величина третьей определяется из уравнения состояния φ = ( p,V,T ) = 0. Если однокомпонентная система гетерогенная, и две фазы находятся в равновесии, то ее состояние определяется заданием значений только одной независимой переменной, поскольку появляется еще одно уравнение связи – уравнение Клапейрона – Клаузиуса 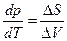 .
.
В точке пересечения уравнений Клапейрона для равновесия двух фаз однокомпонентной системы с третьей (например, лед-пар и вода-пар) все три фазы находятся в равновесии, но эта точка жестко фиксирована и нет ни одной независимой переменной. Эта точка называется тройной точкой для однокомпонентной системы.
Назовем числом степеней свободы число независимых переменных, значения которых можно произвольно изменять в некотором интервале, не меняя числа фаз в находящейся в равновесии многокомпонентной системе. Для однокомпонентной равновесной системы число степеней свободы в зависимости от числа фаз определяется без всякого труда, иное дело многокомпонентные системы, т.е. следует найти общее решение проблемы.
Обозначим надстрочным индексом свойство, относящееся к фазе, подстрочным – свойство, относящееся к компоненту. Тогда условие равновесия системы, состоящей из Ф фаз и «К» компонентов выглядят следующим образом:
условие механического равновесия:
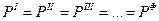
условие термического равновесия :
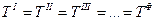
условие химического равновесия :
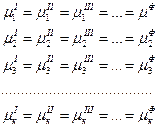
Непосредственный подсчет числа степеней свободы С системы приводит к соотношению : С = 2 + Ф (К – 1) – К(Ф – 1)
Первые два слагаемых получаются из подсчета числа независимых переменных без учета условий химического равновесия, если же учесть и химическое равновесие, то надо вычесть К(Ф – 1). Окончательно имеем
Ф + С = К + 2 правило фаз Гиббса.
Поскольку минимальное значение числа степеней свободы равно нулю (С < 0 не может быть по физическому смыслу), то для нульвариантной системы
Ф = К + 2, и если К = 1, Ф = 3; К = 2 , Ф = 4 и т.д.
Но следует иметь в виду, что если в системе две фазы совпадают по составу, то для концентраций появляется еще одно уравнение связи, и
С = 2 + Ф(К – 1) – К(Ф – 1) – (К – 1) = 1 + 2 –Ф
т.е. такая система ведет себя как однокомпонентная (например, азеотроп) независимо от числа веществ в системе.
Если совпадают по составу три фазы :
С = 2 + Ф(К – 1) – К(Ф – 1) – 2(К – 1) = 4 – К – Ф
При С = 0 , Ф = 4 – К , если К = 1 , Ф = 3 ; если К = 2 , Ф = 2 , получаем противоречие т.к. по условию в системе три фазы. Поэтому три фазы, совпадающие по составу, могут быть только в однокомпонентной системе (тройная точка).
13.2. Диаграммы равновесия некоторых однокомпонентных систем.
Если однокомпонентная система состоит только из одного составляющего вещества (нет химических реакций), то для ее описания достаточно трех переменных : температуры, давления и мольного объема (или обратной величины – молярности). Таким образом диаграмма состояния представляет собой пространственную диаграмму, построенную в прямоугольных осях координат, по одной из осей координат откладываются значения температуры, по другой – значения давлений, по третьей – мольный объем в литр/моль. Располагая подобной системой координат, мы можем с помощью одной точки, называемой фигуративнойточкой всей системы, показать как условия существования системы, т.е. температуру и давление, так и отвечающий им мольный объем. Если при выбранных условиях система распадается на несколько фаз, то фигуративная точка всей системы описывает лишь усредненный мольный объем вещества во всем объеме системы, а каждой фазе соответствует особая фигуративная точка, и состояние всей системы описывается совокупносью нескольких фигуративных точек отдельных фаз.
Фигуративные точки, охватывающие все возможные сочетания р, Т и V вещества в рассматриваемой фазе, образуют некоторую поверхность, называемую полем существования данной фазы. Сочетания подобных полей и образуют объемную диаграмму состояния.
Рассмотрим, например, схему диаграммы состояния двуокиси углерода, построенную без соблюдения масштаба (рис. 13.1). Эта диаграмма образована поверхностью Тв, отвечающей твердой фазе, и поверхностями Ж и Г, состоящими из фигуративных точек жидкой и газообразной фаз. Поверхности Ж и Г при температуре выше критической плавно переходят одна в другую. Состояния, отвечающие одинаковым температурам, отмечены линиями ( изотермами ) 1,2,3,4, критической температуре отвечает изотерма 4.
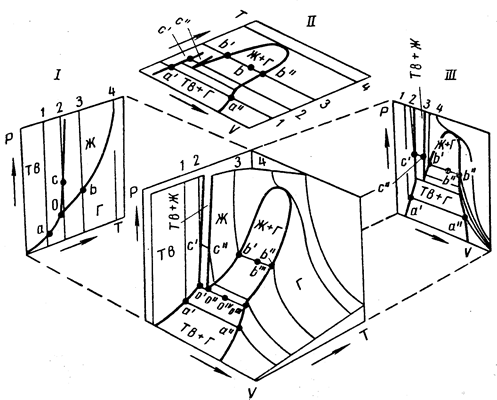
Рис. 13.1. Объемная диаграмма состояния двуокиси углерода (схема). Общий вид и проекции на плоскости p – T (1), v – T (2),
p – v (III)
Совокупность всех прямых линий, соединяющих фигуративные точки двух различных фаз, находящихся при одинаковых температуре и давлении, образует поверхности Тв + Ж, Тв + Г и Ж + Г. Фазы, oтвечающие точкам, соединенным этими линиями, например, точкам а΄ и a΄΄, в΄ и в΄΄, с΄ и с΄΄ находятся в равновесии. Если система состоит из этих двух фаз, то фигуративная точка всей системы в целом, например в΄΄΄, лежит на прямой в΄в΄΄, причем соотношение между количествами каждой из фаз определяется по правилу рычага, на основании отношения длин отрезков в΄в΄΄΄ и в΄΄΄в΄΄.
Изотермы 1, 2, 3, 4 представляют собой сечения указанных поверхностей рядом плоскостей, перпендикулярных оси температур. Одинаковым номерам на разных проекциях отвечает одна и та же изотерма.
Cхема объемной диаграммы состояния воды при низких давлениях дана на рис. 13.2. Эта схема вполне подобна предыдущей с той лишь разницей, что поверхность области льда I отвечает большим мольным объемам, чем поверхность жидкого состояния.
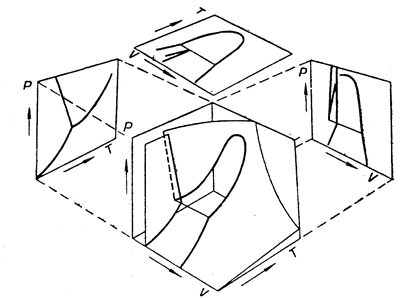
Рис. 13.2 Объемная диаграмма состояния воды при относительно небольших давлениях.
Общий вид и проекции на плоскости р – Т, р - v и T – v (схема)
Проекция диаграммы состояния воды на плоскость р – Т дана ниже. Жидкая вода допускает переохлаждение. Давление пара над переохлажденной водой нанесено на диаграмме пунктиром.
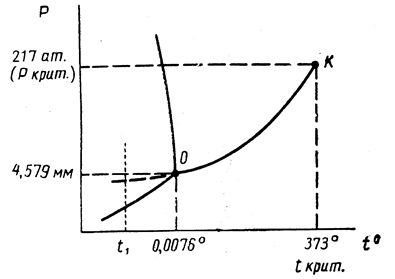
Рис. 13.3. Диаграмма состояния воды в координатах р-Т (схема)
Следует подчеркнуть, что тройная точка равновесного сосуществования пара, жидкости и льда лежит при давлении 4,579 мм рт.ст. и температуре 0,0076° С. 0° С есть температура таяния льда, находящегося под давлением, равным 1 атм. Поскольку кривая равновесного сосуществования льда и воды наклонена влево, температура перехода при давлении насыщенного пара воды, равном лишь 4,579 мм рт.ст., должна быть выше 0° С.
Подобные диаграммы равновесия можно построить для серы и фосфора.
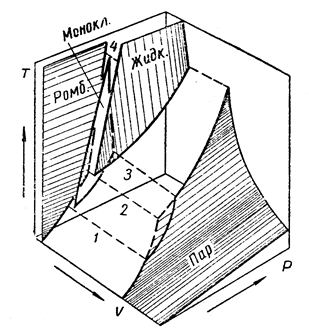
Рис. 13.4. Объемная диаграмма состояния серы (схема). Тройным точкам отвечают пунктиры: 1 – пар,  ; 2 – пар, жидк.,
; 2 – пар, жидк.,  ; 3 – пар, жидк.,
; 3 – пар, жидк., 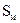 ; 4 – жидк.,
; 4 – жидк., 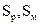
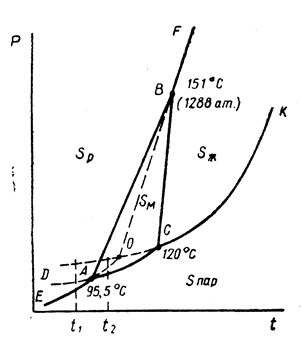
Рис. 13.5. Диаграмма состояния серы в координатах p - t (схема)
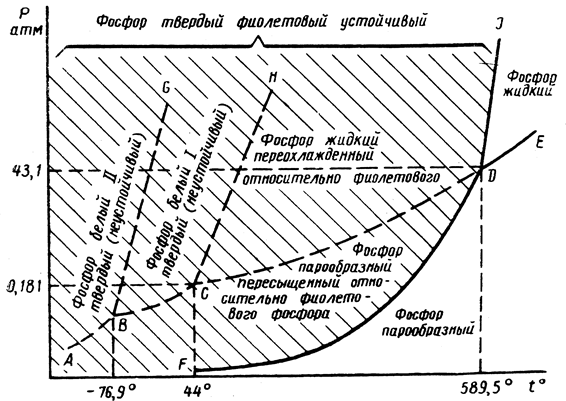
Рис. 13.6. Диаграмма состояния фосфора в координатах p - t (схема)
Объемная диаграмма состояния слишком громоздка и недостаточно удобна в работе. Поэтому на практике вместо полной объемной диаграммы пользуются ее проекциями на одну из трех плоскостей, проходящих через оси координат. Выбор той или другой проекции определяется характером вопроса, для решения которого надо использовать диаграмму состояния. Чаще всего пользуются проекцией I, построенной в координатах Т и р. Проекция I позволяет ответить на вопрос, в каком состоянии находится вещество при заданных условиях. В очень многих случаях этого оказывается достаточно. Мольные объемы фаз на этой проекции никак не отражаются. Зависимость мольных объемов от Т и р можно проследить на проекциях II и III.
13.3. Диаграммы плавкости двухкомпонентных систем.
Будем рассматривать равновесие жидкой фазы двухкомпонентной системы с твердыми фазами (равновесие раствор – пар мы уже рассматривали ранее). Для описания двухкомпонентной системы необходимо пространство четырех координат : Т, р, СА и СВ. Можно уменьшить число измерений до трех, если использовать мольные доли, поскольку хА + хВ = 1, и сделать дальнейшее упрощение, если зафиксировать одну из переменных – либо температуру, либо давление. Это равноценно тому, что представляется сечение полной диаграммы равновесия плоскостью T =const или p = const. Но поскольку одна степень свободы зафиксирована, то правило фаз Гиббса должно быть записано следующим образом :
Ф + С = К + 1
Поскольку влияние давления на состояние равновесия в конденсированных системах незначительно, то обычно рассматривают диаграммы состояния при фиксированном (часто атмосферном давлении).
Когда компоненты А и В не образуют твердых растворов, добавки другого вещества понижают температуру плавления первого, поэтому в результате прибавления В к А или А к В температура кристаллизации понижается, пока обе кривые не встретятся в точке хЕ (рис. 13.7).
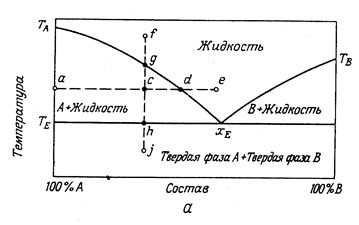
Рис. 13.7.
Выясним физический смысл различных областей диаграммы. Выше кривых ТА хЕ и хЕ ТВ лежит область жидких гомогенных расплавов. Будем теперь охлаждать расплав состава хс, взятый при Тс. Точка g на кривой ТА хЕ соответствует началу кристаллизации из расплава первых кристаллов чистого компонента А. Система из однофазной превращается в двухфазную. В результате кристаллизации компонента А расплав станет богаче компонентом В, а его температура затвердения понизится. Таким образом по мере кристаллизации точка d движется в направлении к точке хЕ, причем все время из расплава выделяются кристаллы А. Когда расплав придет в точку хЕ, начнут выделяться кристаллы вещества В, система становится трехфазной и дальнейшее изменение температуры прекращается. В конце концов весь расплав затвердеет при этой температуре подобно индивидуальному веществу.
Таким образом, в точке хЕ сосуществуют три фазы: чистые твердые А и В и расплав состава хЕ. Затвердевшая смесь, соответствующая точке хЕ, называется эвтектической смесью или эвтектикой, а точка хЕ –эвтектической точкой. При p = const температура и состав эвтектики постоянны и определяются только природой системы ( C = 2 – 3 + 1 = 0 ). Ниже прямой TE лежит область твердых смесей кристаллов A + эвтектика и кристаллов B + эвтектика. Сама эвтектика – это тоже механическая смесь кристаллов веществ А и В, только более тонкая. Если компоненты А и В металлы, то, охлаждая расплав, можно получить твердые образования, используемые в качестве сплавов.
Частный случай системы с образованием трех фаз – растворы некоторых солей в воде (или в другом растворителе). Однако обычно температура плавления соли намного выше температуры плавления растворителя, иногда выше его температуры кипения и даже критической. Поэтому правая часть ветви , проходящая вблизи оси ординат, соответствующей компоненту В на практике не реализуется. Кривая TA хЕ обычно называется кривой растворимости; она характеризует процесс выпадения кристаллов вещества В, т.е. соли. Справа от хЕ располагается область составов пересыщенных растворов, которые легко превращаются в гетерогенную смесь, состоящую из насыщенного раствора и кристаллов соли. Эвтектика, образующаяся в водных растворах солей называется криогидратом. Криогидрат – это тонкая смесь льда и кристалликов соли.
Однако при охлаждении расплава из него не всегда выпадают кристаллы чистых твердых веществ. В некоторых случаях компоненты А и В образуют твердые растворы.
Рассмотрим, как изображается графически состояние систем, обладающих ограниченной взаимной растворимостью компонентов в твердом состоянии (рис. 13.8). При охлаждении расплава из него начинают выделяться кристаллы твердого раствора. .В точкеэвтектикирасплав затвердевает, образуя эвтектику, представляющую собой тонкую смесь твердых растворов. При дальнейшем понижении температуры состав двух сосуществующих друг с другом твердых растворов изменяется. В точке эвтектики сосуществуют три фазы переменного состава : расплав и два твердых раствора. При p = const в точке Ts система условно нонвариантна.
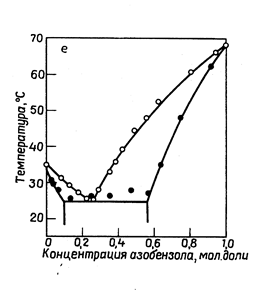
| 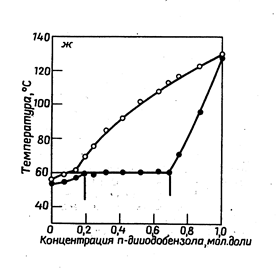
|
| Рис.13.8. Азоксибензол- азобензол | Рис.13.9. п –хлориодбензол – n-дииодбензол |
Существует и другой тип диаграмм плавкости систем, обладающих ограниченной взаимной растворимостью компонентов в твердом состоянии (рис. 13.9).
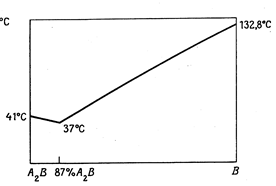
Во многих случаях кривая плавкости двухкомпонентных систем проходит через один или несколько максимумов. Так как температура затвердевания всякого вещества понижается при прибавлении посторонних примесей, то форму таких кривых можно объяснить тем, что в точке максимума образуется химическое соединение, температура плавления которого понижается при прибавлении к нему как компонента А, так и компонента В. Если образовавшееся соединение устойчиво как в жидком, так и в твердом состоянии, то точку максимума называют конгруэнтной (рис. 13.10).
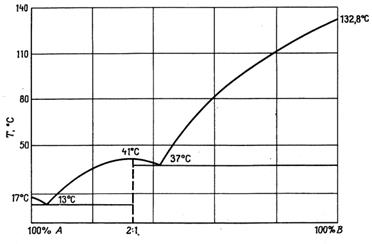
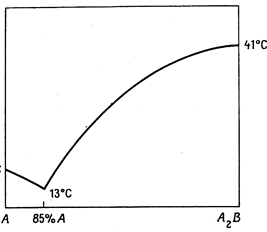
| 
|
Рис. 13.10. Система уксусная кислота (А) + мочевина (В), в которой образуется межмолекулярное соединение  .Общая диаграмма разделена на две, на одной из которых показано вещество А.
.Общая диаграмма разделена на две, на одной из которых показано вещество А.
Если химическое соединение очень устойчиво и при плавлении совсем не диссоциирует, то кривые, располагающиеся слева и справа от конгруэнтной точки, соответствуют двум разным процессам, а именно кристаллизации АтВп из его раствора в компоненте А, и кристаллизации АтВп из расплавов, содержащих преимущественно вещество В. Поэтому такие кривые затвердевания резко различаются по своим наклонам, а конгруэнтная точка соответствует острому максимуму.
Если же соединение при плавлении частично диссоциирует, то при составах, лежащих слева от конгруэнтной точки, в расплаве присутствуют некоторые количества компонента В, а при составах расположенных справа – компонента А. Поэтому кривая ликвидуса имеет плавный ход с размытым максимумом.
В точке плавления твердое соединение сосуществует с жидкостью того же состава, так как система однокомпонентна. Плоскость диаграммы, таким образом, делится на следующие области :
выше кривой ликвидуса находится область, в которой расположены точки составов жидкости;
ниже лежат области гетерогенности, в которых расплав сосуществует последовательно с кристаллами А, кристаллами соединения АтВп и с
кристаллами В.
Точки Э1 и Э2 представляют собой эвтектики, образованные компонентом А с соединением АтВп и соединением АтВп с В.
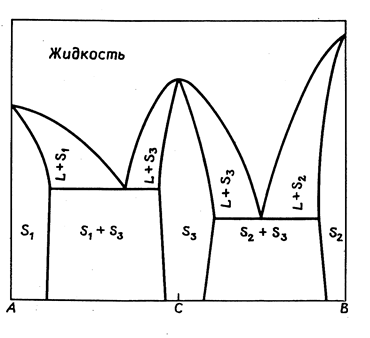
Рис. 13.11.
На рис. 13.11 изображена диаграмма состояния бинарной системы, в которой существует химическое соединение и вещества обладают в твердом состоянии ограниченной взаимной растворимостью друг в друге. Твердый раствор образован компонентом А и соединением С; или веществами В и С. Формально диаграмма как бы распадается на две составные части.
Однако при затвердевании расплава, состоящего из двух компонентов, может образовываться не только соединение, устойчивое в обеих фазах, но и соединение, которое может существовать только в соприкосновении с расплавом, содержащим избыток одного из компонентов. В этом случае на кривой температур плавления вместо максимума появляется точка перегиба. Но при рассмотрении диаграммы такого типа удобно подразумевать наличие скрытого максимума. Диаграмма плавкости системы, в которой образуется неустойчивое соединение, изображена на рис. 13.12. Здесь отрезок кривой от температуры плавления В до точки D представляет собой геометрическое место точек состава расплавов, из которых кристаллизуется чистый компонент В. Из всех расплавов, точки составов которых располагаются на кривой от эвтектики до D, кристаллизуется химическое соединение V. Если бы это соединение было устойчивым в жидкой и в твердой фазе, то на кривой плавкости его температуре плавления соответствовал бы максимум (точка C). При T D химическое соединение распадается на расплав D и компонент В. Точка TD не соответствует настоящей температуре плавления М : в ней состав расплава отличен от состава твердой фазы. Такую температуру называют инконгруэнтной (инконгруэнтная точка). Система в инконгруэнтной точке инвариантна, так как сосуществуют три фазы : расплав состава xN , кристаллы В и М.
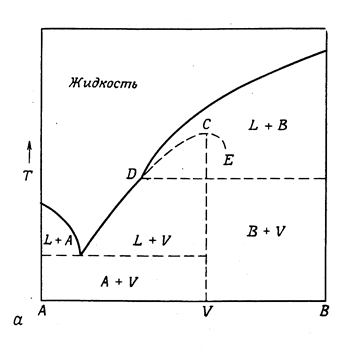
Рис. 13.12.
13.4. Экспериментальное построение диаграмм плавкости. Физико-химический анализ.
Данные, необходимые для построения диаграмм плавкости бинарных систем, получаются методом термического анализа. Если измерять температуру двухкомпонентного расплава при постепенном охлаждении через одинаковые промежутки времени и результаты наносить на график время – температура (t -T), то получатся кривые скорости охлаждения (рис. 13.13). При охлаждении расплава чистого вещества на кривой скорости понижения температуры появляется площадка («остановка») (отрезок А или В ), обусловленная выделением теплоты кристаллизации расплава в точке его затвердевания.
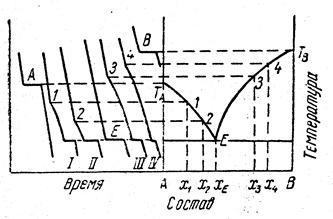
Рис.13.13. Пример построения диаграммы состояния двухкомпонентной
системы по кривым охлаждения: система, образующая одну эвтектику.
При наличии одной эвтектики и при условии, что компоненты не образуют твердых растворов, кривые охлаждения смеси имеют иной вид. При охлаждении расплава состава 1 кривая время – температура имеет один излом, вызванный началом кристаллизации компонента А; по мере хода кристаллизации А скорость охлаждения меняется по кривой. Начиная с точки ТЕ, температура во времени остается постоянной, этот участок соответствует кристаллизации эвтектики, как целого. Далее кривая характеризует скорость охлаждения твердой фазы.
Вполне аналогичную картину можно получить для расплава состава 4 с той лишь разницей, что в этом случае участок кривой (линия ТВ Е на рисунке) будет соответствовать кристаллизации компонента В. Чем ближе по составу расплав к эвтектике, тем короче участки кристаллизации В и тем длиннее участки кристаллизации эвтектики, так как масса эвтектики увеличивается. Если рассмотреть охлаждение расплава состава самой эвтектики Е, то на кривой понижения температуры окажется только одна площадка.
Изломы кривых t -T позволяют построить диаграмму плавкости. Если провести горизонталь через точку ТЕ и отложить по вертикали вниз отрезки, пропорциональные или равные длинам участков кристаллизации эвтектики, то, проведя прямые через точки концов отрезков, можно получить так называемый треугольник Таммана. Если в результате опытов получен такой треугольник, это означает, что никаких особых точек, кроме эвтектики на кривых плавкости нет. Подобным же образом можно проводить исследование двухфазных систем путем их нагревания. Рисунок 13.14 показывает пример построения диаграммы равновесия системы с химическим соединением, плавящимся инконгруентно.
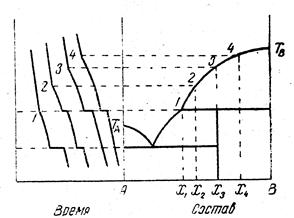
Рис.13.14. Пример построения диаграммы состояния двухкомпонентной системы по кривым охлаждения:
система образует химическое соединение, плавящееся инконгруэнтно.
Термический анализ систем типа жидкость – твердая фаза является частным случаем применения весьма распространенного метода физико – химического анализа бинарных и многокомпонентных систем. В основе метода физико-химического анализа лежит исследование зависимости какого-либо свойства системы от ее состава при условиях, гарантирующих возможность однозначного определения значения свойства по концентрации компонентов и, наоборот, установления состава системы по значению заданного свойства (при
T , p = const или одного из этих параметров). В бинарных и трехкомпонентных системах такая зависимость обычно выражается графически. Кривые свойство – состав получают путем экспериментального изучения исследуемого свойства при нескольких заданных составах системы. Если анализируется гомогенная система, то основываясь на предположении о непрерывном и плавном изменении значения того или иного свойства при изменении содержания одного из компонентов, методом интерполяции по определенному значению свойства устанавливается состав однородной системы, т. е. решается задача, обратная выполняемой при построении калибровочного графика. Если же система при изменении состава претерпевает фазовые превращения, то каждому изменению количества или природы фаз будет соответствовать излом на кривой состав – свойство, как это и происходит при термическом анализа.
Для проведения физико – химического анализа могут быть использованы самые разнообразные свойства системы, например, вязкость, теплоемкость, теплопроводность, электропроводность, коэффициент сжимаемости и т.д. Наиболее часто с этой целью строят кривые зависимости плотности или показателя преломления от состава. Последнее объясняется тем, что значения этих свойств можно определить с большой точностью. Кроме того, измерение показателя преломления требует весьма малой затраты времени.
Дата добавления: 2015-07-30; просмотров: 3265;
