Если газ реальный и работа его изотермического изменения объема

А_{реальн.} измерена, то можно записать, что

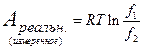
где f – некоторое свойство реального газа, которое определяет в таком простом соотношении его реальную измеряемую работу изотермического изменения объема. Назовем это свойство летучестью (иногда называют фугитивностью : английское fugacity – летучесть). Таким образом, для реального газа можно записать (Гилберт Ньютон Льюис, 1907) :

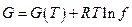
а для его химического потенциала в смеси

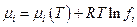
Задача упростилась, но не намного, поскольку необходимо указать способы определения летучести газа в конкретных условиях. Но прежде чем перейти к этой проблеме дадим один пример экспериментального определения величины работы изотермического изменения объема реального газа.

В таблице приведены результаты измерений электродвижущих сил Е гальванического элемента:

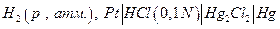
в зависимости от давления водорода при 25 ⁰С и рассчитанные по этим экспериментальным данным величины летучести водорода при соответствующих давлениях следующим образом.

р, атм	Е, мВ	Е(р) – Е(1)		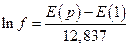f, атм
1,00	399,0			1,0
37,8	445,6	46,6	3,630	37,7
51,6	449,6	50,6	3,942	51,5
110,2	459,6	60,6	4,721	112,3
204,7	468,3	69,6	5,422	226,3
386,6	478,4	79,4	6,185	485,5
439,3	480,4	81,4	6,341	567,4
556,8	484,4	85,4	6,653	774,8
568,8	485,0	86,0	6,699	811,9
701,8	489,1	90,1	7,019	1117,4
707,8	489,9	90,9	7,081	1189,3
731,8	489,3	90,3	7,034	1135,0
754,4	490,3	91,3	7,112	1226,9
862,2	493,2	94,2	7,338	1537,9
893,9	493,8	94,8	7,385	1611,6
974,5	496,3	97,3	7,580	1957,9
1035,2	497,5	98,5	7,673	2149,8

Как мы узнаем ниже, разность Е(р) – Е(1) умноженная на 2F ( F – число Фарадея, равное 96487 кулонов/г-экв ) как раз равна работе расширения водорода при 25 0С от давления р до 1 атм

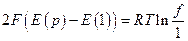
подстановка численных значений F, R и T дает

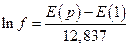
Таким образом летучесть, хотя и косвенно, в принципе можно измерить. Как видно из последней колонки таблицы, при давлениях выше 50 атм летучесть водорода начинает отличаться от давления и при 1000 атм превосходит давление примерно вдвое. Итак, летучесть это такое давление, которое должна оказывать идеально-газовая система, чтобы производить такое же действие, что и реальная система.

Понятно, что разность между летучестью и давлением стремится к нулю по мере приближения состояния реального газа к идеальному, т.е. при бесконечно малом давлении, тогда

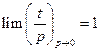
Для характеристики отклонения свойств реального газа от идеального вводится отношение летучести к давлению, которое называется коэфициентом летучести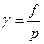

Заметим также - летучесть конденсированной фазы в гетерогенной системе равна летучести насыщенного пара, находящегося в равновесии с конденсированной фазой.

14.2. Методы расчета летучести.

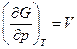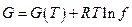Так как , а , то при T=const

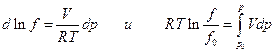
Если задано уравнение состояния реального газа , то интеграл можно вычислить аналитически. Пусть, например,

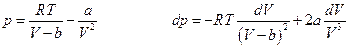Тогда

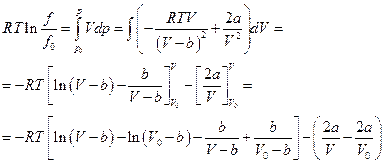
Устремим 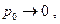тогда 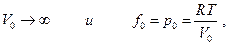отсюда

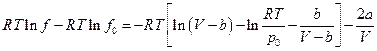и

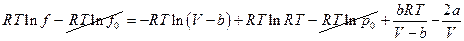
Окончательно: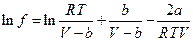

т.е. при данной температуре Т вычисляем V при данном давлении и подставляем в полученную формулу.

Можно поступить и следующим образом. Если при данной температуре Т измерены мольные объемы реального газа в зависимости от давления, то эту зависимость можно представить в виде

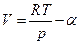
где α – экспериментальная объемная поправка, тогда очевидно, что

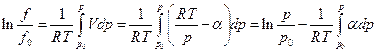
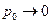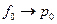Если , то и

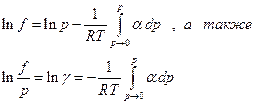
Интеграл можно вычислить графически. Приведем два примера :

СО ,273 К		NH3 , 423 K
Р, атм		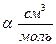f, атм		Р, атм		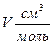	f
	11,0	0,999			-
	12,5	24,62			760,7	106,8	35,5
	10,6	46,60			226,7	120,5	73,0
	8,5	72,13			66,40	165,9	89,5
	6,3	95,38			46,88	126,7	98,0
	2,0	141,7			40,24	75,47
	-2,1	189,0			37,36	49,44
	-9,0	298,0			34,22	23,65
	-3,9	408,3			32,68	10,72
	-7,4	547,6			31,41	3,31
	-19,8	714,1
	-17,6	1152,0
	-24,3	1778,0
	-24,8	2183,0
	-25,3	2663,0

Стоит заметить, что при небольших давлениях 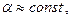следовательно

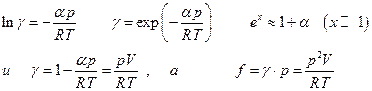
Полученные выражения для γ и f приближенные и годятся примерно до

50 - 100 атм.

14.3. Использование закона соответственных состояний.

Любое уравнение состояния реального газа должно учитывать тот факт, что при некоторой температуре газ должен конденсироваться и может находиться в равновесии с жидкой фазой. Анализ показывает, что при критической температуре должны соблюдаться два условия

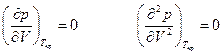
это приводит к тому, что правило фаз Гиббса для системы в критической точке однокомпонентной системы должно быть записано как

С = 1 – Ф

в связи с тем, что число степеней свободы уменьшается на 2. Следовательно в критической точке в системе находится одна фаза и число степеней свободы равно нулю, т.е.критическая точка однокомпонентной системы представляется фундаментальной точкой.

Уравнение состояния Ван-дер-Ваальса можно представить как кубическое относительно объема

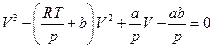
В критической точке при Т_кр и р_кр три корня уравнения равны, т.е.

а так же

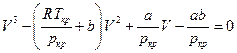
Сравнивая коэффициенты при одинаковых степенях V имеем :

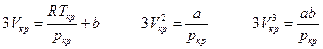
и для a , b и R в явном виде

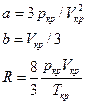
Подстановка констант в исходное уравнение Ван-дер-Ваальса дает

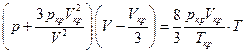
После умножения почленно на 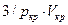имеем

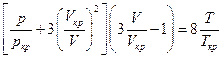
Ведем обозначения 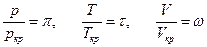( 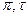и ω носят название приведенных давления, температуры и объема), отсюда :

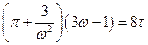
Заметим, что в полученное уравнение не входят какие-либо индивидуальные характеристики веществ, следовательно оно годится для любых веществ и носит название приведенного уравнения Ван-дер-Ваальса.

Очевидно, что при одинаковых 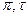и ω свойства веществ должны быть одинаковы (закон соответственных состояний). Следовательно, можно предположить, что и коэффициенты летучести γ должны быть одинаковыми, поэтому зависимость γ = f (π, τ) должна иметь универсальный характер. Эта зависимость вычислена и в справочниках представляется как в виде таблиц, так и графиков. Для водорода, гелия и неона необходимо вводить поправку :

Т_кр + 8, р_кр + 8 атм.

Пример : аммиак, Т_кр = 405,6 К; р_кр = 111,5 атм при температуре 425 К, τ = 1,043 и

р, атм	π	γ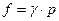
	-	1,0	1,0
	0,359	0,9
	0,897	0,7
	1,345	0,55
	1,794	0,47
	2,690	0,35
	3,587	0,30
	5,381	0,27
	7,175	0,26
	8,969	0,25

Сравнение с предыдущей таблицей показывает, что закон соответственных состояний справедлив при давлениях примерно до 500 атм.

14.4. Летучесть компонента в смеси реальных газов.

Для парциальной летучести компонента f_i в смеси реальных газов мы можем записать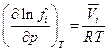

где 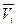- парциальный мольный объем i-ого газа в смеси. При фиксированной температуре можем получить

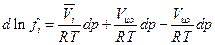
где V_ид –мольный объем идеального газа при тех же р и Т, что и парциальный мольный объем компонента i. Далее

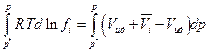и

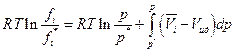
При бесконечно малом давлении р^* выполняется закон Дальтона р_i = p^*x_i

где x_i – мольная доля i-ого газа, тогда

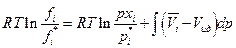
но если р^*→ 0, то 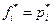и

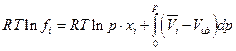
Но для непосредственных расчетов полученное уравнение затруднительно использовать, поскольку парциальным мольным объемом i-ого газового компонента в широком интервале температур и давлений располагать трудно. Поэтому поступим следующим образом : приравняем парциальный мольный объем компонента смеси мольному объему компонента при том же общем давлении : 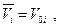тогда

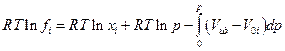
и оказывается, что два последних слагаемых правой части равенства представляют собой 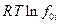,где f_0i - летучесть чистого компонента i (см. выше). Следовательно :

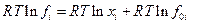или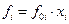

то-есть летучесть компонента смеси равна летучести чистого компонента при давлении, равном общему давлению, умноженной на мольную долю этого компонента в смеси.