Как было отмечено ранее, выражение
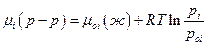
пригодно для любых растворов, и для реальных растворов. Льюис предложил отношение pi /poi обозначать через ai и называть термодинамической активностью. Итак для реального раствора:
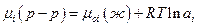
Так как 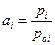 , то активность компонента в растворе с мольной долей xi может быть определена по измерению парциального давления насыщенного пара компонента над раствором. Активность – это такая концентрация данного компонента в идеальном растворе, при которой он в последнем имеет такой же химический потенциал, что и в реальном растворе. Введенная Льюисом (1907) новая функция состояния – активность не раскрывает причин отклонения данного раствора от идеального поведения. Она только упрощает формальное математическое описание термодинамически неидеальных растворов. Следует отметить, что понятие активности очень важное обобщение и активность вещества в многокомпонентной системе можно измерить или вычислить, даже если оно нелетуче.
, то активность компонента в растворе с мольной долей xi может быть определена по измерению парциального давления насыщенного пара компонента над раствором. Активность – это такая концентрация данного компонента в идеальном растворе, при которой он в последнем имеет такой же химический потенциал, что и в реальном растворе. Введенная Льюисом (1907) новая функция состояния – активность не раскрывает причин отклонения данного раствора от идеального поведения. Она только упрощает формальное математическое описание термодинамически неидеальных растворов. Следует отметить, что понятие активности очень важное обобщение и активность вещества в многокомпонентной системе можно измерить или вычислить, даже если оно нелетуче.
Кроме активности в термодинамике реальных растворов вводится коэффициент активности 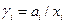 . Поскольку
. Поскольку
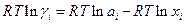
то коэффициент активности ( точнее RTlnγi ) представляет собой работу переноса 1 моля i –ого компонента из идеального раствора в данный реальный раствор.
Итак для неидеальных растворов
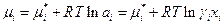
где 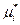 - химический потенциал компонента в стандартном состоянии, когда ai =1, является функцией только температуры и давления, тогда как γι –функция не только температуры и давления, но и концентрации. Чтобы дополнить определение коэффициента активности γι необходимо указать условия, при которых γι становится равным единице. Это можно сделать двумя способами, поскольку при хι→ 1 мы приближаемся к закону Рауля, при хι→0 к закону Генри.
- химический потенциал компонента в стандартном состоянии, когда ai =1, является функцией только температуры и давления, тогда как γι –функция не только температуры и давления, но и концентрации. Чтобы дополнить определение коэффициента активности γι необходимо указать условия, при которых γι становится равным единице. Это можно сделать двумя способами, поскольку при хι→ 1 мы приближаемся к закону Рауля, при хι→0 к закону Генри.
| Численно сравнивать химические потенциалы вещества мы можем только, если они отнесены к одному и тому же стандартному состоянию. |
Таким образом, используют два способа выбора стандартного состояния: симметричный и несимметричный.
Способ 1 (симметричный). За стандартное состояние каждого компонента принимается состояние чистого вещества и в этом состоянии активность каждого компонента принимается равной 1, т.е. коэффициент активности γι → 1, когда
хι→ 1, тогда 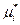 равен мольной энергии Гиббса чистого компонента i при данных температуре и давлении. Этот способ применяется, когда агрегатное состояние раствора совпадает с агрегатными состояниями его компонентов при данной температуре.
равен мольной энергии Гиббса чистого компонента i при данных температуре и давлении. Этот способ применяется, когда агрегатное состояние раствора совпадает с агрегатными состояниями его компонентов при данной температуре.
Способ 2 (несимметричный) Этот способ удобно использовать, когда нельзя изменять мольные доли некоторых компонентов вплоть до единицы, например, для растворов газов или твердых тел в жидкостях. Тогда для растворителя и растворенного вещества принимаются разные условия :
γ1 (растворитель) → 1 при х1 (растворитель) → 1
а коэффициент активности растворенного вещества приближается к единице, когда его концентрация приближается к нулю
γ2 (р-рен. в-во) → 1 при х2 (р-рен. в-во) → 0
Далее
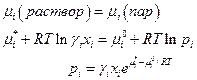
I: если γ1 = 1 при хi = 1, то 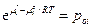 и при любых хi :
и при любых хi :
pi = γi xi poi cледовательно при  и выражение переходит в закон Рауля.
и выражение переходит в закон Рауля.
II. если 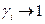 при
при 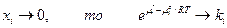 (константа Генри)
(константа Генри)
и pi → ki xi при xi → 0 , а при любых xi
pi = γi ki xi
Пример : растворы ацетон – эфир при 30 0С, р в торр
| Ацетон | Способ 1. γi = pi / poi xi | Способ 2 | ||||||
| x2 | p1 | x1p01 | γ1 | p2 | x2p02 | γ2 | k2x2 | 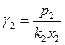
|
| 1,00 | - | (1,000) | ||||||
| 0,2 | 1,03 | 56,6 | 1,59 | 117,6 | 0,766 | |||
| 0,4 | 1,13 | 113,2 | 1,31 | 235,2 | 0,630 | |||
| 0,5 | 1,21 | 141,5 | 1,19 | 0,575 | ||||
| 0,6 | 258,4 | 1,28 | 170,0 | 1,12 | 0,538 | |||
| 0,8 | 129,2 | 1,56 | 1,04 | 0,499 | ||||
| 1,0 | - | 1,00 | 588* | (0,481) |
* -константа Генри
Как видно из таблицы симметричный способ показывает, что имеются в наличии положительные отклонения от закона Рауля, а последняя колонка показывает отклонение от закона Генри.
10.3. Интегральные и парциальные мольные величины.
Будем задавать состояние системы и ее массу с помощью выбора в качестве переменных Т, р, п1…..пк. Пусть Z - некоторая экстенсивная термодинамическая величина ( Z= U, H, F, G, S, V, Cp, CV и др.), тогда при вышеуказанном выборе независимых переменных
Z = Z (T, p, n1……nk )
Определим теперь парциальную мольную величину 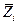 соотношением:
соотношением:
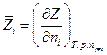
Величина 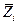 характеризует изменение функции Z при добавлении к бесконечно большому количеству системы 1 моля i – ого компонента в условиях постоянства Т , р и чисел молей других компонентов. Поскольку речь идет об очень большой (бесконечно большой) системе, состояние ее при внесении 1 моля компонента остается неизменным (можно было бы рассматривать процесс добавления бесконечно малого количества i –ого компонента к системе конечного размера, но перейти к изменению функции Z в расчете на 1 моль добавляемого компонента i). При xi = 1 парциальная мольная величина Z обращаетсяв мольную величину Z для индивидуальноговещества i.
характеризует изменение функции Z при добавлении к бесконечно большому количеству системы 1 моля i – ого компонента в условиях постоянства Т , р и чисел молей других компонентов. Поскольку речь идет об очень большой (бесконечно большой) системе, состояние ее при внесении 1 моля компонента остается неизменным (можно было бы рассматривать процесс добавления бесконечно малого количества i –ого компонента к системе конечного размера, но перейти к изменению функции Z в расчете на 1 моль добавляемого компонента i). При xi = 1 парциальная мольная величина Z обращаетсяв мольную величину Z для индивидуальноговещества i.
Всистеме, содержащей несколько компонентов, величина 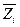 определяется не только природой i –ого компонента, но и свойствами системы в целом по той причине, что молекулы i –ого компонента взаимодействуют с молекулами других компонентов;в неявном виде величина
определяется не только природой i –ого компонента, но и свойствами системы в целом по той причине, что молекулы i –ого компонента взаимодействуют с молекулами других компонентов;в неявном виде величина 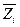 учитывает все изменения, происходящие в системе при внесении i –ого компонента. Парциальная мольная величина – функция состояния системы и может быть представлена как
учитывает все изменения, происходящие в системе при внесении i –ого компонента. Парциальная мольная величина – функция состояния системы и может быть представлена как
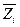 =
= 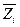 (T, p, x1……xk-1)
(T, p, x1……xk-1)
Заметим, что производная от экстенсивной функции по числу молей i –ого компонента является парциальной мольной величиной только в случае постоянства вышеуказанных независимых переменных:
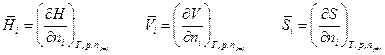
Химический потенциал компонента μi может быть представлен производной от различных термодинамических функций
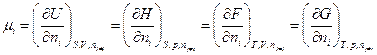
но только последняя производная является парциальной мольной величиной,
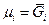 .
.
Экстенсивные свойства – однородные функции первого порядка относительно чисел молей компонентов, и по теореме Эйлера для однородных функций
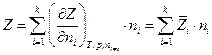
Поскольку полный дифференциал Z
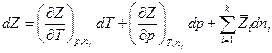 и
и
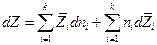
то легко получить обобщенное уравнение Гиббса-Дюгема :
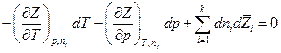
Если 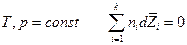 , в частности если
, в частности если 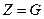 , то
, то
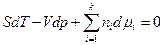 и при
и при

Между парциальными мольными величинами существуют те же соотношения, что и между интегральными, например,
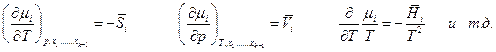
Будем рассматривать в дальнейшем бинарную систему (наиболее частый случай) и пусть общее количество вещества в системе 1 моль, т.е. 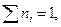 тогда
тогда
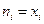 и
и 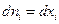 , а поскольку
, а поскольку

Для бинарной системы Z = Z (T, p, xi ) и
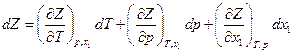
С другой стороны
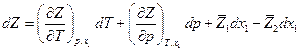
Сравнив оба выражения, имеем

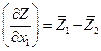 Кроме того
Кроме того
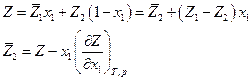
Функцией смешения 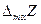 называется изменение Z при образовании раствора из чистых компонентов. Для 1 моля раствора
называется изменение Z при образовании раствора из чистых компонентов. Для 1 моля раствора
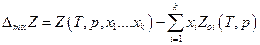
Заметим, что для чистого компонента 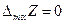
Парциальная мольная функция смешения
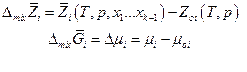
Очевидно, что 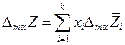
Для бинарной системы
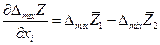
Очевидно, что касательная в точке х1 к зависимости интегральной 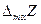 от х1 отсекает на ординатах х1 = 0 и х1 = 1 отрезки, равные соответственно
от х1 отсекает на ординатах х1 = 0 и х1 = 1 отрезки, равные соответственно
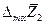 и
и 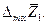
Выведем еще одну важную формулу. Обозначим через А некоторую функцию смешения 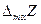 , тогда уравнение Гиббса-Дюгема дает:
, тогда уравнение Гиббса-Дюгема дает:
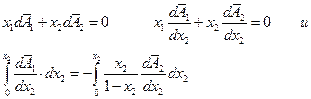
Левый интеграл дает 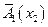 в точке х2, правый после взятия по частям:
в точке х2, правый после взятия по частям:
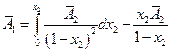 или
или
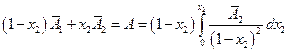
и 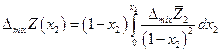
т.е. измерив парциальную мольную функцию смешения можно сразу вычислить и интегральную величину.
Заметим, что при вычислении химического потенциала компонента по измеренной активности другого удобнее интегрировать коэффициент активности поскольку его логарифм при xi → 0 не стремится в бесконечность
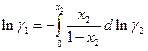
Избыточной функцией смешения называется разность между функцией смешения рассматриваемого раствора и идеального раствора той же концентрации.
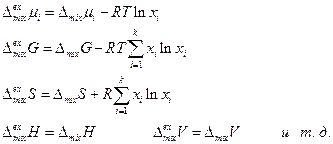
Дата добавления: 2015-07-30; просмотров: 1527;
