Глава 9. Смеси жидкостей.
9.1 Давление насыщенного пара растворителя над раствором. Закон Рауля.
В дальнейшем изложении будем рассматривать бинарные растворы и обозначать свойства, относящиеся к растворителю, индексом «1» (к чистому «01»), а к растворенному веществу индексом «2» (для чистого «02»).
В паре над раствором обычно содержатся все компоненты раствора, и давление насыщенного пара над раствором равно сумме парциальных давлений компонентов. При относительно невысоких давлениях паровую фазу можно рассматривать как идеальную газовую смесь, т.е.считать, что насыщенный пар описывается уравнением состояния идеального газа и выполняется закон Дальтона. Отдельные компоненты раствора могут быть нелетучи при данной температуре и отсутствовать в паре. Как общее давление пара над раствором, так и парциальные давления компонентов зависят от температуры и состава раствора.
Система раствор – насыщенный пар является термодинамически равновесной, поэтому химические потенциалы компонента в растворе и паре равны: 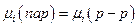 . Химический потенциал растворителя в растворе
. Химический потенциал растворителя в растворе 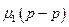 меньше, чем химический потенциал чистого жидкого растворителя
меньше, чем химический потенциал чистого жидкого растворителя 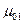 при тех же условиях (температура), иначе раствор не может образоваться. Но поскольку
при тех же условиях (температура), иначе раствор не может образоваться. Но поскольку
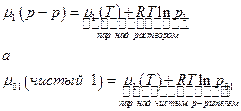
то парциальное давление пара растворителя в паровой фазе над раствором всегда меньше, чем давление насыщенного пара чистого растворителя (естественно, при одинаковых условиях). Если температура постоянна, то понижение парциального давления пара растворителя называется раствором (по сравнению с давлением пара чистого растворителя) будет зависеть от состава раствора.
Рауль ( в 1882 – 1890 г.г.) экспериментально установил, что относительное понижение давления пара растворителя над раствором равно мольной доле растворенного вещества:
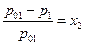
Нужно отметить, что реально закон Рауля соблюдается только для достаточно разбавленных растворов (х2 достаточно мало). Растворы же, подчиняющиеся закону Рауля при всех концентрациях и температурах, называются идеальными (совершенными) растворами.
Поскольку 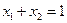 , то закон Рауля можно записать в виде
, то закон Рауля можно записать в виде

т.е. парциальное давление насыщенного пара растворителя над раствором пропорционально его мольной доле.
9.2. Давление насыщенного пара растворенного вещества над раствором. Закон Генри.
Если насыщенный пар над бинарным раствором обладает свойствами смеси идеальных газов, тогда для его компонентов мы можем записать
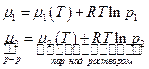
Если температура постоянна, то дифференцирование дает

Уравнение Гиббса-Дюгема в расчете на 1 моль смеси:
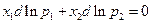 , отсюда
, отсюда


По закону Рауля

Тогда
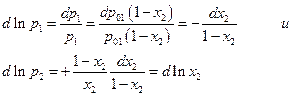
После интегрирования имеем
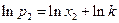 и
и
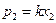 (закон Генри)
(закон Генри)
т.е. парциальное давление пара растворенного вещества над раствором пропорционально мольной доле растворенного вещества х2. Коэффициент пропорциональности «к» носит название константы Генри. Очевидно, что закон Генри выполняется только в той области концентраций, где для растворителя выполняется закон Рауля. Если раствор идеален, то закон Рауля выполняется для всех составов 0≤х1≥1, следовательно и закон Генри будет выполняться также во всех областях концентраций 1≥х2≥0, но тогда при х2 = 1, к=р02..
Таким образом для идеальных растворов мы можем записать
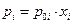 . Для неидеальных растворов закон Рауля (а, следовательно, и закон Генри в форме р2 =кх2 ) будет выполняться только в области малых концентраций растворенного вещества ( х2 →0 ). Такие реальные (не идеальные ) растворы называются предельно разбавленными или бесконечно разбавленными растворами и нужно понимать, что для них р1 = р01∙х1, р2 = кх2 причем к ≠ р02.
. Для неидеальных растворов закон Рауля (а, следовательно, и закон Генри в форме р2 =кх2 ) будет выполняться только в области малых концентраций растворенного вещества ( х2 →0 ). Такие реальные (не идеальные ) растворы называются предельно разбавленными или бесконечно разбавленными растворами и нужно понимать, что для них р1 = р01∙х1, р2 = кх2 причем к ≠ р02.
9.3. Состав насыщенного пара идеального раствора.
Будем рассматривать бинарный раствор и обозначим через х мольную долю растворенного вещества в растворе, тогда 1-х –мольная доля растворителя.
Состав пара над раствором выразим аналогично: у –мольная доля растворенного вещества, 1-у – мольная доля растворителя в паре. Очевидно, далее, что общее давление пара над раствором равно сумме парциальных давлений компонентов:
р = р1 + р2
и если раствор идеальный, то
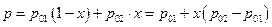
т.е. общее давление насыщенного пара идеального раствора является линейной функцией состава раствора.
Далее концентрация растворенного вещества в паре согласно закону Дальтона 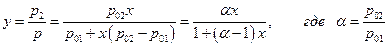
(α – называют относительной летучестью).
Мы видим, что состав насыщенного пара не совпадает с составом идеального раствора т.е. у ≠ х . Составы совпадают только в следующих случаях :
α = 1, х = 1, х = 0. Поскольку
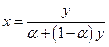 и, следовательно,
и, следовательно,
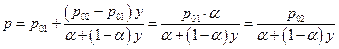
Таким образом, общее давление пара над идеальным раствором не является линейной функцией состава пара.
9.4. Диаграммы равновесия. Правило рычага
. Термодинамической диаграммой называется графическое изображение термодинамических равновесных состояний системы на плоскости с прямолинейными координатами при условии, что по осям координат откладываются термодинамические параметры ( Т, р, V, U, S, x и их производные). Диаграммой равновесия или диаграммой состояния называется зависимость термодинамических параметров фаз от состава сосуществующих фаз. Фигуративная точка – любая точка на плоскости диаграммы состояния и характеризующая валовой состав системы ( х ) и ее некоторый термодинамический параметр. Таким образом диаграммы состояния бинарных систем изображают области существования различных фаз системы, и чтобы изобразить диаграмму на плоскости рассматривают их сечения соответствующей плоскостью p = Const или T = Const и получают диаграммы равновесия давление – состав при постоянной температуре или температура – состав при постоянном давлении.
Если раствор идеальный, то диаграмму давление – состав при T = Const построить достаточно просто. Действительно, давление в системе в зависимости от состава раствора(жидкой фазы) описывается уравнением
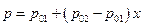 а в зависимости от состава пара
а в зависимости от состава пара
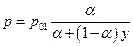
Положим для определенности 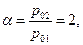 тогда можем составить следующую таблицу:
тогда можем составить следующую таблицу:
| у = 0 | р = р01 | Заметим, что и х и у изменяются в одной и той же области значений между 0 и 1, поэтому общее давление пара и как р = р(х) и как р = р(у) мы можем изобразить на одной и той же диаграмме. |
| у = 0,25 | р = 1,145р01 | |
| у = 0,50 | р = 1,333р01 | |
| у = 0,75 | р = 1,600р01 | |
| у = 1,00 | р = 2,000р01 = р02 |
Легко сообразить, что р = р(х) это прямая линия, соединяющая точки р01 при х = 0 и р02 при х = 1.
Относительные количества фаз, находящихся в равновесии, подчиняются одному простому правилу.
Пусть общее количество вещества в системе равно 1 молю, а общее количество компонента 2 равно х0 . Если в жидкой фазе мольная доля растворенного вещества равна х, а в насыщенном паре у, то уравнение материального баланса дает
x0 = my + ( 1 – m )x,
где m – количество (моль) пара, 1-m –количество (моль) жидкости. Вычтем из обеих частей равенства сначала x, а затем y, получаем:
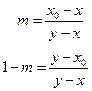
Разделив равенства почленно друг на друга имеем:
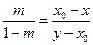
Разности х0 – х и у – х0 равны отрезкам, на которые фигуративная точка системы делит отрезок, соединяющий составы фаз, находящихся в равновесии ( этот отрезок носит название ноды или коноды), поэтому получаем следующее правило: массы находящихся в равновесии фаз обратно пропорциональны отрезкам, на которые фигуративная точка системы делит ноду. Вышеприведенное равенство можно записать в виде:
т( у – х0 ) = ( 1 – т ) ( х0 – х )
это выражение представляет условие равновесия рычага, точка опоры которого находится в х0, поэтому это правило и называется правилом рычага. Оно справедливо для любых диаграмм состояния.
9.5. Температура кипения идеального раствора.
Определим температуру кипения раствора в качестве такой, при которой общее давление пара над раствором становится равным внешнему давлению. Если раствор идеальный, то при постоянном внешнем давлении
p = p1 + p2 = p01 ( T ) ( 1-x ) + p02 ( T ) ·x = Const
и поскольку

то, во-первых нет линейной зависимости между составом раствора х и температурой кипения Т при p = Const, во-вторых, необходимо знать свойства компонентов – константы уравнения Клапейрона-Клаузиуса А1, А2, В1 и В2. Тем не менее, диаграмму состояния температура кипения – состав для идеального раствора можно построить для данного p = Const, так как
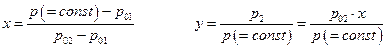
Пример: тетрахлориды олова и углерода образуют идеальный раствор и при р=760 торр температуры кипения чистых равны соответственно 114 и 77 0С. Можно составить следующую таблицу для составов раствора и пара системы, температуры кипения которой будут находиться между 77 и 114 0С
| t,0C | ||||||||
| SnCl4, p01 | - | |||||||
| CCl4, p02 | - | |||||||
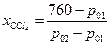
| 1,000 | 0,868 | 0,531 | 0,274 | 0.072 | 0,000 | ||
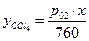
| 1,000 | 0,955 | 0,777 | 0,523 | 0,178 | 0,000 | ||
Эффективность разделения компонентов раствора путем перегонки, очевидно, зависит от величины различия составов жидкости и пара, т.е. от разности у – х. Исследуем этот вопрос для идеального раствора.
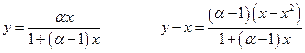
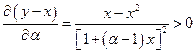
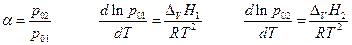
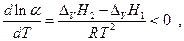 поскольку
поскольку
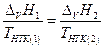 ( правило Трутона ), и если p02 > p01 , то
( правило Трутона ), и если p02 > p01 , то
THTK(1) > THTK(2) , следовательно Δv H1 > Δv H2 .Отсюда можно сделать вывод, что перегонку раствора необходимо производить при как можно более низких температурах, то-есть при пониженном общем давлении.
9.6. Законы Коновалова.
Диаграммы равновесия жидкость – пар как идеальных, так и реальных растворов подчиняются ряду простых закономерностей. Их легко получить, использовав уравнение Гиббса-Дюгема:

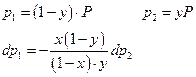
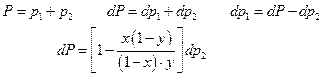
Разделим правую и левую части полученного уравнения на dx :
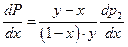
Поскольку производная 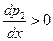 , т.к. парциальное давление второго компонента в паре всегда растет с ростом его содержания в жидкости, то знак производной
, т.к. парциальное давление второго компонента в паре всегда растет с ростом его содержания в жидкости, то знак производной 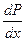 зависит от знака разности у – х . Если y > x, то
зависит от знака разности у – х . Если y > x, то 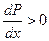 и получаем I закон Коновалова: в паре над раствором преобладает по сравнению с раствором тот компонент, прибавление которого к раствору приводит к возрастанию полного давления пара.
и получаем I закон Коновалова: в паре над раствором преобладает по сравнению с раствором тот компонент, прибавление которого к раствору приводит к возрастанию полного давления пара.
Если же dP/dx = 0 , то это возможно только, когда y = x,и получаем
II закон Коновалова : в экстремумах полного давления пара (или температур кипения) раствор и насыщенный пар имеют одинаковый состав. Очевидно, что в этом случае разделение компонентов раствора путем перегонки становится невозможным. Такие растворы носят название азеотропных или нераздельно кипящих.
Приведем примеры смесей с максимум и минимумом общих давлений
паров.
Смеси ацетон-сероуглерод, 50 0С
| % мольн.CS2 | 
| 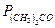
| P | |
| в жидкости | в паре | торр | торр | торр |
| 343,8 | 343,8 | |||
| 6,24 | 25,06 | 110,7 | 331,0 | 441,7 |
| 13,30 | 40,12 | 206,5 | 308,3 | 514,8 |
| 28,69 | 54,52 | 328,7 | 274,2 | 602,9 |
| 44,74 | 60,94 | 390,4 | 250,2 | 640,6 |
| 61,61 | 65,50 | - | - | 653,6 |
| 67,13 | 66,80 | 438,0 | 217,0 | 655,0 |
| 82,80 | 72,07 | 463,9 | 180,2 | 645,1 |
| 92,42 | 80,29 | 490,0 | 120,3 | 610,3 |
| 96,92 | 89,02 | 502,0 | 62,0 | 564,0 |
| 512,3 | 512,3 |
Смеси хлороформ-ацетон, 35,17 0С
| % мольн. СНCl3 | 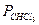
| 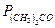
| P | |
| в жидкости | в паре | торр | торр | торр |
| 344,5 | 344,5 | |||
| 12,03 | 6,23 | 19,9 | 300,2 | 320,1 |
| 18,53 | 10,39 | 31,9 | 275,4 | 307,3 |
| 27,04 | 17,27 | 50,2 | 240,3 | 290,5 |
| 36,06 | 26,46 | 72,3 | 200,8 | 273,1 |
| 50,83 | 45,57 | 115,3 | 137,6 | 252,9 |
| 58,12 | 56,32 | 139,9 | 108,5 | 248,4 |
| 66,10 | 68,17 | 169,6 | 79,2 | 248,8 |
| 80,47 | 85,36 | 224,2 | 38,4 | 262,6 |
| 91,75 | 95,35 | 267,1 | 13,0 | 280,1 |
| 293,1 | 293,1 |
Образование азеотропов причиняет много неприятностей при разделении смесей путем перегонки. Хорошо известен азеотроп вода – этанол 95,6 % масс этанола и температурой кипения 78,15 0С. однако помимо химической абсолютизации этанола с помощью обработки, например, гидридом кальция можно поступить по-другому. Бензол, этанол и вода образуют тройной азеотроп с 74,1, 18,5 и 7,4 % масс соответственно и температурой кипения 65 0С, избыток бензола можно удалить также в качестве азеотропа (32,4 % С2Н5ОН и 67,6 % С6Н6, температура кипения 68,3 0С) и затем перегнать С2Н5ОН при 78,4 0С
(99,9 %). Однако можно значительно уменьшить требуемое (десятикратное по отношению к воде) количество бензола, если учесть, что тройной азеотроп является гетерогенным и ниже 28 0С расслаивается на верхний слой (85 %), содержащий 85,6 % С6Н6, 11,6 % С2Н5ОН и 2,8 % Н2О и нижний слой с 8,1 % С6Н6, 53,1 % С2Н5ОН и 40,6 % Н2О. Если все время возвращать верхний слой в кипящую смесь, расход бензола можно уменьшить по крайней мере на порядок. Заметим также, что азеотроп можно разрушить изменением внешнего давления. Например, при 6,3 атм и 135,5 0С в азеотропе спирт – вода всего 1 % масс воды.
9.7. Химический потенциал компонента в идеальном растворе.
Если раствор находится в равновесии с паром, то химические потенциалы компонентов в растворе и в паре над ним одинаковы:

Если пар над раствором обладает свойствами идеального газа, то
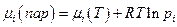
где рi –парциальное давление i –ого компонента в паре.
Для чистого i –ого компонента аналогично:

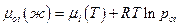
где рoi –давление насыщенного пара чистого жидкого i –ого компонента при той же температуре, что и раствор. Вычитая из верхнего выражения нижнее, имеем:
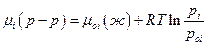
В этом уравнении химический потенциал i –ого компонента в растворе выражен через химический потенциал чистого i –ого компонента (или что то же мольную энергию Гиббса) и отношение давлений насыщенного пара компонента над раствором и над чистой жидкостью при той же температуре. Следует заметить, что полученное выражение справедливо для любых растворов, поскольку при его выводе не сделано никаких предположений относительно характера раствора.
Если раствор идеальный, то по закону Рауля pi = poi ·xi , следовательно
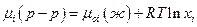
При постоянных давлении и температуре энергия Гиббса 1 моля раствора может быть представлена как
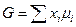
а для идеального раствора
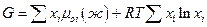
но первая сумма это энергия Гиббса системы до процесса смешения, следовательно изменение энергии Гиббса при образовании 1 моля идеального раствора может быть представлено как
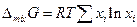
а так как образование идеального раствора из жидкостей не сопровождается тепловым эффектом, то и изменение энтропии на 1 моль раствора
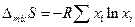
9.8. Растворимость газов в жидкостях.
Нет принципиальной разницы между растворами газов в жидкостях и растворами жидкостей в жидкостях.Растворение сопровождается уменьшением объема системы и выделением теплоты порядка величины теплоты конденсации газа в жидкость.
Опытным путем был установлен закон Генри (1803 г.): при постоянной температуре растворимость данного газа в данном растворителе прямо пропорциональна его давлению над раствором : р2 = кх2 (чем больше к тем меньше растворимость данного газа при данном давлении). Растворимость газа, как видно, сильно растет с ростом давления, и обычно уменьшается с ростом температуры. Если газ и жидкость образуют идеальный раствор во всей области концентраций, то 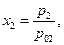 где р02 – давление чистого газа 2 в равновесии с его жидкой фазой при температуре раствора, откуда видно, что мольная доля газа в идеальном растворе не зависит от природы растворителя. Для вычисления р02 необходимо экстраполировать давление насыщенного пара чистой жидкости 2 на температуру раствора. Например, экстраполяция давления пара жидкого метана на температуру 298 К дает р02 = 370 атм., откуда получаем для
где р02 – давление чистого газа 2 в равновесии с его жидкой фазой при температуре раствора, откуда видно, что мольная доля газа в идеальном растворе не зависит от природы растворителя. Для вычисления р02 необходимо экстраполировать давление насыщенного пара чистой жидкости 2 на температуру раствора. Например, экстраполяция давления пара жидкого метана на температуру 298 К дает р02 = 370 атм., откуда получаем для 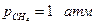 идеальную растворимость х2 = 0,0027. Для сравнения растворимость СН4 в гексане равна 0,0031, в ксилоле 0,0026.
идеальную растворимость х2 = 0,0027. Для сравнения растворимость СН4 в гексане равна 0,0031, в ксилоле 0,0026.
Для реальных растворов сопоставление растворимости различных газов в одинаковых условиях не позволяет установить простой закономерности. В общем здесь действует правило : подобное растворяется в подобном, т.е. полярные газы легче растворяются в полярных растворителях, чем неполярных. Далее неполярные газы, обладающие более высокой критической температурой, т.е. легче сжижаемые, легче растворяются в неполярных жидкостях, чем газы сжижаемые труднее.Если происходит химическое взаимодействие газа и растворителя, как, например, в растворах H2S, CO2, HCl, NH3 в воде , то растворимость резко повышается.
Растворимость, х2 ×104, 20 0С, р2 = 1 атм.
| H2 | N2 | CO | O2 | CH4 | CO2 (0 0C) | NH4 (0 0C) | Cl2 (0 0C) | |
Идеальная 
| 12,8 | 13,2 | ||||||
| в CCl4 | 3,27 | 6,42 | 8,86 | 12,0 | 28,6 | - | ||
| в CH3OH | 1,57 | 2,35 | 3,25 | 3,18 | 7,1 | - | ||
| в H2O | - | 0,15 | 0,12 | 0,13 | 0,23 |
Растворимость в воде, 0 0С, 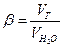 , 1 атм.
, 1 атм.
| H2 | N2 | O2 | CH4 | Ar | CO2 | H2S | SO2 | HCl | NH3 | |
| Ткр | 20,5 | |||||||||
| β | 0,0214 | 0,0232 | 0,0492 | 0,0556 | 0,0561 | 1,713 | 4,62 | 79,8 |
Если в одном и том же растворителе одновременно растворяются два газа, невзаимодействующие химически друг с другом и с растворителем, то они не оказывают влияние на растворимость друг друга. Заметим, что кислород примерно в два раза более растворим в воде, чем азот, что оказывается важным для организмов, живущих в воде. При цикле последовательных растворений и выделений воздуха, выделяющийся газ постепенно обогащается кислородом
| N цикла | ………. | |||||
| % О2 | 33,3 | 47,5 | ……….. | 95,0 | 97,3 | |
| % N2 | 66,7 | 57,5 | ……….. | 5,0 | 2,7 |
Растворимость газов в воде обычно уменьшается при добавлении других растворимых веществ, в частности электролитов. Это явление, получившее название «высаливания», впервые было обнаружено И.М.Сеченовым. Он получил уравнение, выражающее влияние концентрации электролита на растворимость газов
 ln C =ln C0 – bm
ln C =ln C0 – bm
где С0 – растворимость данного газа в чистой воде, С – растворимость его при той же температуре в растворе электролита, имеющим концентрацию « т » (моль/л),
в – эмпирическая постоянная, зависящая от природы газа, электролита и температуры. Ионы электролита как бы уменьшают из-за гидратации массу «свободной» воды.
9.9. Виды взаимной растворимости жидкостей.
1. Полная (неограниченная) смешиваемость.
2. Ограниченная смешиваемость.
3. Практически полная нерастворимость.
Примером ограниченной смешиваемости является система фенол-вода:
| t 0C | масс % фенола | Выше 65,84 0С фенол и вода смешиваются во всех отношениях. Ряд других систем также ведут себя подобным образом и наблюдаемая | |
| I слой | II слой | ||
| 72,16 | 8,36 | ||
| 71,28 | 8,66 | ||
| 69,90 | 9,22 | ||
| 67,63 | 9,91 | ||
| 54,83 | 59,22 | - | |
| 61,30 | - | 14,87 | критическая температура является |
| 62,55 | 51,87 | - | |
| 62,74 | - | 19,35 | верхней температурой, так как выше ее |
| 65,24 | 44,09 | - | |
| 65,79 | - | 30,21 | две жидкости смешиваются во всех |
| 65,84 | 34,23 | 34,23 |
отношениях. Но в ряде случаев
наблюдается нижняя критическая температура так триэтиламин и вода смешиваются во всех отношениях ниже 18 0С, а выше этой температуры происходит резко выраженное расслоение смесей. Нижняя критическая точка имеется и у системы вода – 2,4,6 триметилпиридин (5,7 0С, 82,8 % масс воды). В системе никотин – вода наблюдаются обе критические точки – 60,8 0 и 208,0 0С и 34 % масс никотина.
Полной нерастворимости жидкостей друг в друге не существует, вопрос только в методах обнаружения малых примесей. Даже растворимость воды в ртути составляет величину примерно 10 -5 моль/л или около 10 –6 % по массе.
Общее давление пара в системе двух несмешивающихся жидкостей равно сумме давлений пара чистых жидкостей
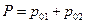
следовательно такая система будет кипеть при температуре ниже. чем температура кипения самой легкокипящей. Так бензальдегид имеет температуру кипения 178 0С, а в смеси с водой перегоняется при 98 0С. Массовое отношение компонентов в дестиллате можно легко рассчитать по уравнению:
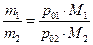
где т – массовые количества компонентов в паре, М – их мольные массы. По этому уравнению легко рассчитать необходимое количество воды, если осуществлять перегонку с водяным паром.
Дата добавления: 2015-07-30; просмотров: 2749;
