Уравнение Клапейрона – Клаузиуса

6.1. Определения.

Фазой называется совокупность частей системы, обладающих одинаковыми термодинамическими свойствами. Система, состоящая из одной фазы, называется гомогенной, из двух или более – гетерогенной. Фаза более общее понятие, чем индивидуальное вещество. Система может состоять из одного вещества, но быть гетерогенной (вещество находится в системе в виде разных агрегатных состояний или кристаллических модификаций). Система может быть гомогенной, но содержать несколько химических соединений, пример этого – растворы.

Назовем составляющими веществами системы такие химические соединения, которые могут быть выделены из системы и существовать отдельно от нее. Назовем независимыми компонентами такие составляющие вещества, концентрации которых могут изменяться независимо. Если в системе не протекают химические реакции, то все вещества, составляющие систему, являются независимыми компонентами.

Но в случае фактического протекания химических реакций концентрации только части веществ могут изменяться независимо, поэтому число независимых компонентов равно числу составляющих веществ минус число химических реакций, которые фактически протекают в систее.

6.2. Условия равновесия и направление самопроизвольного процесса в однокомпонентной гетерогенной системе.

Пусть гетерогенная однокомпонентная система имеет две фазы (΄) и (˝), а мольные энергии Гиббса компонента в каждой из фаз G^΄ и G^˝ соответственно. Пусть давление и температура постоянны, а изменение чисел молей компонента в фазе (´) равно 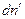, в фазе (´) 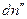, тогда изменение энергии Гиббса системы равно:

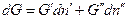
Если система закрытая, то 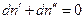, и

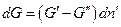
При равновесии 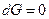, а это возможно, когда

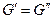
т.е при равновесии мольные энергии Гиббса компонента в фазах равны.

Самопроизвольный процесс в системе может протекать только в сторону уменьшения энергии Гиббса системы, т.е. 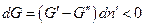. Положим, для определенности, что 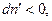тогда 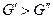, если же

Это значит, что компонент самопроизвольно переходит из той фазы, где его мольная энергия Гиббса больше, в ту фазу, где его мольная энергия Гиббса меньше.

Изменим давление и температуру на бесконечно малые величины dT и dp, тогда очевидно, что если система остается равновесной и гетерогенной

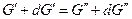
следовательно, и .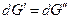

6.3. Уравнение Клапейрона-Клаузиуса.

Очевидно, что

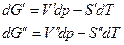
где V’,V’’,S’,S” мольные объемы и мольные энтропии компонента в фазах (‘) и (“). Из условий равновесия

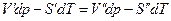или

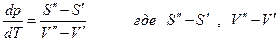изменеие энтропии и объема при переходе 1 моля компонента из фазы ( ‘ ) в фазу ( “ ), т.е. это мольные изменения энтропии и объема фазового превращения.

Учитывая, что фазовое превращение рассматривалось как равновесное и изотермическое, то

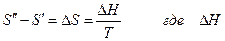- теплота фазового превращения и окончательно

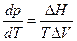уравнение Клапейрона –Клаузиуса

Заметим, что в уравнении Клапейрона ΔH и ΔVотносятся к одноименным процессам и на одно и тоже количество вещества.

6.4. Фазовое равновесие в конденсированных системах.

Конденсированной системой называется такая, в которой не имеется в наличии газообразная фаза, а только твердые или жидкие или те и другие вместе.

Наиболее интересным является равновесие кристалл ↔ жидкость. Поскольку теплота плавления всегда положительна, знак производной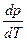

будет зависеть от знака ∆V. Для большинства веществ ∆V>0 (V_ж > V_кр), и производная положительна, т.е. температура лавления будет расти с ростом давления. Однако у некоторых веществ (H₂O, Ga, Bi, Sb, Ge, Si и др.) при плавлении происходит уменьшение объема, V_ж < V_кр , и температура плавления понижается с повышением давления. Так для воды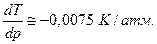

Если предположить, что для конденсированных систем ∆H и ∆V не зависят ни от давления, ни от температуры, то уравнение Клапейрона-Клаузиуса легко интегрируется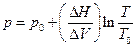

Интересным является рассмотрение равновесия

С (графит) →С (алмаз)

Использование справочных данных для энтальпий образования и энтропий графита и алмаза дает для этого превращения

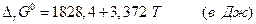
откуда видно, что при любых температурах 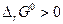. Но поскольку

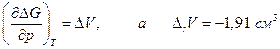
то с увеличением давления ∆_rG должна уменьшаться и при данной температуре графит и алмаз находятся в равновесии, тогда когда ∆_rG = 0. Предположив, что ∆V не зависит от давления, получим после интегрирования

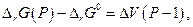откуда

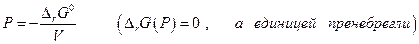
Подставив численные значения ∆_rG⁰ и ∆V получим

Р (атм) = 9448 + 17,42 Т

При 300 К Р=14670 атм

1000 К Р=26870 атм

1500 К Р=35580 атм ,

т.е. равновесные давления имеют порядок десятков тысяч атм.

Далее

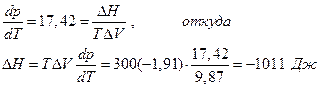
и мы видим, что при высоком давлении поменялся даже знак теплового эффекта. Действительно, возьмем уравнение Гиббса-Гельмгольца

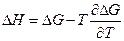и возьмем производную по давлению :

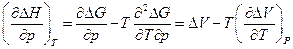
после интегрирования и ряда упрощений имеем

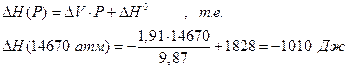
6.5. Интегрирование уравнения Клапейрона-Клаузиуса для процесса парообразования.

Переход жидкости в пар называют испарением, обратный процесс

конденсацией. Испарение твердых тел называют возгонкой или сублимацией, обратный – кристаллизацией. Пар, который находится в равновесии с конденсированной фазой, называется насыщенным паром.

Поскольку теплота парообразования положительна, а мольный объем пара больше мольного объема конденсированной фазы, это значит, что производная в уравнении Клапейрона-Клаузиуса

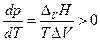
т.е. с ростом температуры давление насыщенного пара увеличивается.

При температурах, далеких от критических, мольный объем пара много больше мольного объема конденсированной фазы, поэтому последним можно пренебречь, а если в этой области температур насыщенный пар подчиняется уравнению состояния идеального газа, то

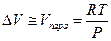
и уравнение Клапейрона-Клаузиуса можно представить в виде

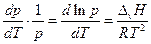
В нешироком интервале температур теплоту испарения можно считать постоянной и взятие определенного интеграла дает:

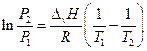
Таким образом, если известна ∆_v H, то, зная давление насыщенного пара вещества при одной температуре, можно рассчитать давление насыщенного пара при другой температуре. С другой стороны, определив давление насыщенного пара при двух (по крайней мере) температурах, можно рассчитать теплоту испарения.

Взятие неопределенного интеграла дает (при ∆_v H = const)

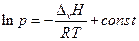или

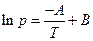
где А и В – константы, характерные для данного вещества. Это уравнение, линейное в координатах ln p – 1/T, дает прямую линию в значительном интервале температур. Более точным является уравнение Антуана

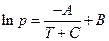где А, В, С – константы.

Практически полезным может оказаться правило Трутона: энтропия испарения вещества в нормальной точке кипения (при 1 атм.) равна приблизительно 90 Дж/моль.К. Тогда в уравнение Клапейрона-Клаузиуса входит только одна константа Т_нтк – температура нормальной точки кипения:

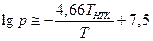
По этому уравнению удобно рассчитывать температуру перегонки органических соединений под пониженным давлением. Однако следует отметить, что правило Трутона соблюдается только для «нормальных» жидкостей, т.е. таких молекулы которых не ассоциированы в жидкой фазе (как у воды за счет водородных связей), а также если пары не состоят из полимерных или диссоциированных молекул.

Для уксусной кислоты прямые определения теплоты испарения в калориметре при температуре кипения СН₃СООН равной 391 К дает величину 406Дж/г. С другой стороны при 363 К давление пара 293 торр, при 391 К 760 торр. Заменив производную в уравнении Клапейрона-Клаузиуса отношением конечных приращений имеем

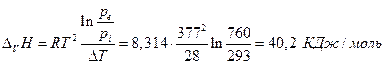
Мольная масса СН₃СООН равна 60, тогда из калориметрических данных

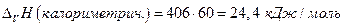
Расхождение между этими двумя значениями связано с тем, что для получения одного моля пара необходимо испарить больше, чем 60 г СН₃СООН, следовательно мольная масса пара СН₃СООН равна

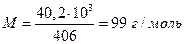
отсюда легко сообразить, что пары уксусной кислоты в этом температурном интервале димеризованы примерно на 2/3.

Насыщенный пар обладает еще рядом интересных свойств. Рассмотрим некоторые из них.

Пусть в гетерогенной системе при температуре Т находится 1 моль вещества, причем в равновесии находятся m молей пара и 1-m молей жидкой фазы. Пусть теплоемкость пара С_п, жидкости С_ж, изменяем температуру от Т до T+dT, при этом испаряется масса жидкости dm, тогда затраты тепла dQ можно представить в виде соотношения:

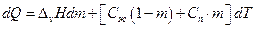
Разделим правую и левую части на Т, имеем

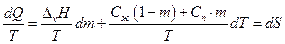
следовательно, справедливо:

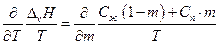
после дифференцирования имеем

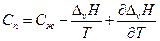
По уравнению Кирхгоффа

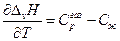и

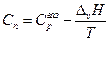
т.е. теплоемкость насыщенного пара не равна изобарной теплоемкости того же газообразного вещества.

Следует также иметь в виду, что введение постороннего (инертного) газа изменяет давление насыщенного пара при неизменной температуре, даже если газ не растворяется в жидкости. Это происходит вследствие влияния общего давления на свойства конденсированной фазы (возрастает ее мольная энергия Гиббса). Действительно, при T=const

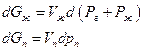
где Р_г – давление постороннего газа, Р_ж давление насыщенного пара, V_ж и V_п -мольныеобъемы жидкости и пара. Поскольку по условию равновесия dG_ж =dG_п

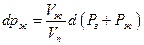
Взятие интеграла от Рг = 0 до Р_г приводит к уравнению

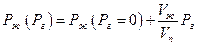
Поскольку дробь V_ж/V_n невелика (для воды при 373 К она равна 5,9∙10^-4), то влияние постороннего газа сказывается только при высоких давлениях.

Например, для воды под давлением водорода при 373 К

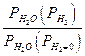
	эксп		1,018	1,19	1,66	2,35
расч		1,015	1,12	1,35	1,802

Глава 7. Термодинамические свойства многокомпонентных систем. Растворы. Химический потенциал.

7.1. Определения.

Раствором называется гомогенная, молекулярно-дисперсная система, состав которой можно изменять непрерывно в некотором конечном или бесконечном интервале.

По агрегатному состоянию растворы разделяются на тврдые, жидкие и газообразные. Если растворитель и растворенное вещество имеют разные агрегатные состояния, то растворителем рассматривают обычно то вещество, агрегатное состояние которого совпадает с агрегатным состоянием раствора. Если же компоненты раствора и раствор имеют одинаковое агрегатное состояние, то за растворитель считают то вещество, которого больше, хотя для термодинамики это безразлично.

Состав раствора измеряется его концентрацией. Существуют следующие основные определения концентрации:

мольная доля ( х ) – число молей вещества в 1 моле раствора;

моляльность ( m ) – число молей растворенного вещества в 1000 г растворителя;

молярность ( с ) – число молей растворенного вещества в 1 л раствора;

массовое содержание ( р ) – число грамм растворенного вещества в 100 г раствора.

В основном мы будем пользоваться мольной долей. Очевидно, что

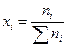, а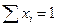

Если М₀ и М мольные массы растворителя и растворенного вещества, а d – плотность раствора, г/см³, то переход от одной концентрации к другой можно представить следующими формулами (раствор, естественно, бинарный):

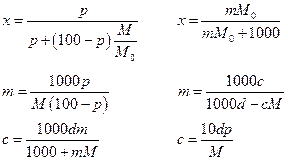
7.2. Характеристические функции многокомпонентных систем.

Первый и второй законы термодинамики, из которых следуют фундаментальные уравнения, были получены для закрытых систем, т.е. систем, процессы в которых не приводят к изменению количества компонентов. Реально же чаще встречаются системы, в которых при различных процессах изменяются количества компонентов. Это может происходить, скажем, при фазовых превращениях или вследствие протекания химической реакции. При этом может изменяться состав как отдельных частей, так и системы в целом.

Поэтому внутренняя энергия (и другие функции состояния) открытых систем будут изменяться не только за счет сообщения системе теплоты и произведенной системой работы, но и за счет изменения состава системы. Следовательно для открытых систем характеристические функции будут функциями не только их двух естественных переменных, но и функциями числа молей всех веществ , составляющих систему:

U = U ( S, v, n₁……………….n_k )

H = H ( S, p, n₁ ………….. n_k )

F = F ( T, v, n₁…………… n_k )

G = G ( T, p, n₁……………n_k )